在空间问题中,描述问题中的应力、形变及位移时,在某些情况下(如减振器节流阀片变形和应力问题),采用柱坐标系(ρ,φ,z)往往使问题得以简化。如图2-14所示,如果弹性体所有的应力分量、形变分量及位移分量都只是ρ和z的函数,而不随φ改变,则此种问题称为空间轴对称问题。轴对称问题的弹性体的形状一般为圆柱体或半空间体,如果随着φ改变,也就相应地称为空间非轴对称问题。
下面导出空间轴对称问题的基本方程。
首先导出轴对称问题的平衡微分方程。
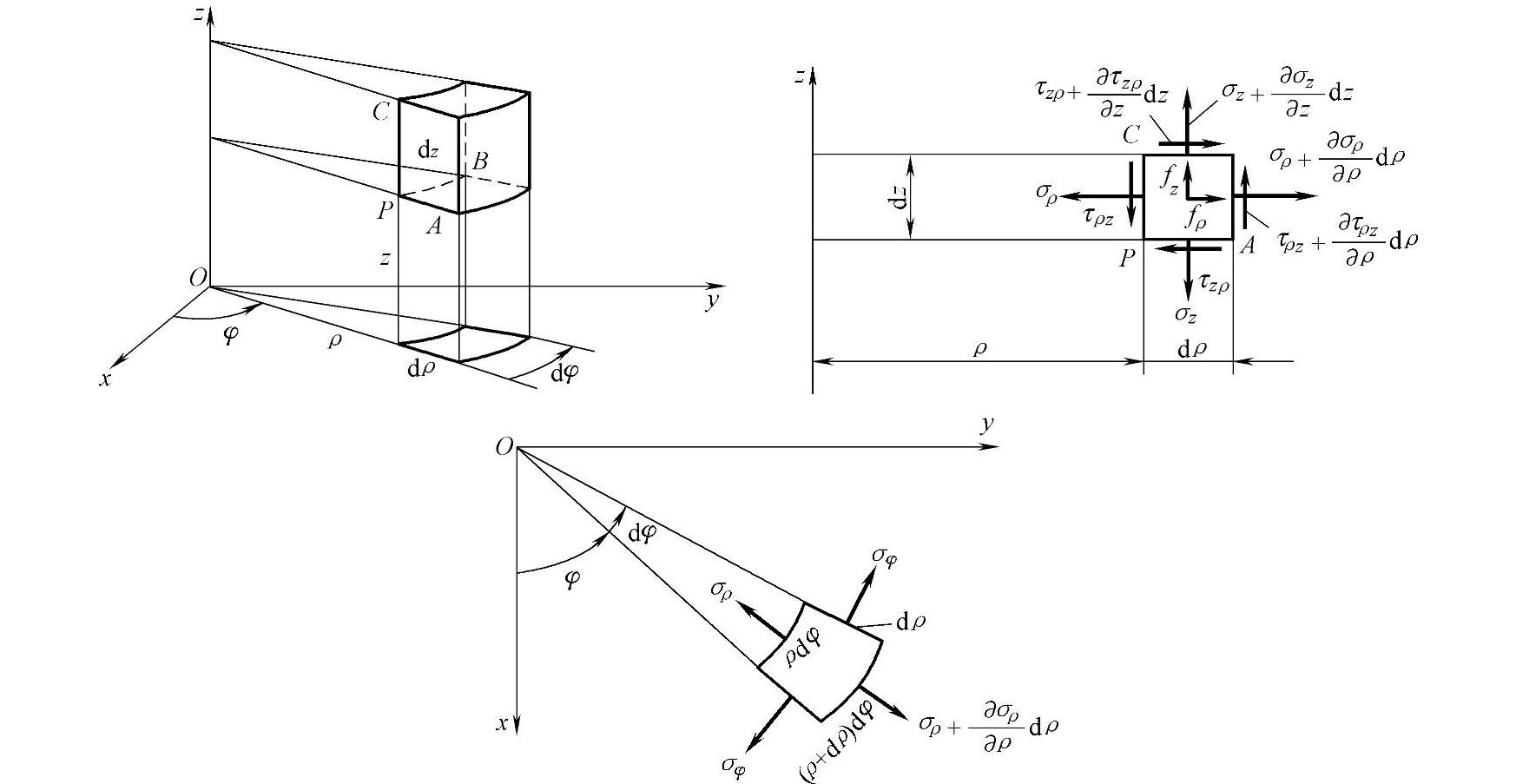
图2-14 弹性体在柱坐标系下的受力情况
如图2-14所示,用相距dρ的两个圆柱面,互成dφ角的两个铅直面及相距dz的两个水平面,从弹性体中割取一个微小六面体PABC。沿着ρ方向的正应力,称为径向正应力,用σρ表示;沿φ方向的正应力称为环向正应力,用σφ表示;沿着z方向的正应力,称为轴向正应力,仍然用σz表示;作用在圆柱面上而沿着z方向的切应力用τρz表示,作用在水平面上而沿着ρ方向的切应力用τzρ表示。根据切应力互等定理,τρz=τzρ。由于对称性,τρφ=τφρ及τzφ=τφz都不存在。这样,总共有4个应力分量:σφ、σρ、σz和τρz(=τzρ),一般都是ρ和z的函数。
如果六面体的内圆柱面上的正应力为σρ,则由于应力随坐标ρ的变化,外圆柱面上的正应力为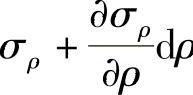 。如果六面体下面的正应力为σz,则上面的正应力为
。如果六面体下面的正应力为σz,则上面的正应力为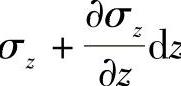 。同样,内面及外面的切应力分别为τρz及
。同样,内面及外面的切应力分别为τρz及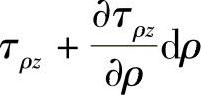 ,下面和上面的切应力分别为τzρ和
,下面和上面的切应力分别为τzρ和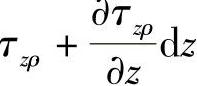 。径向的体力分量用fρ表示,轴向的体力分量用fz表示。
。径向的体力分量用fρ表示,轴向的体力分量用fz表示。
将六面体所受的各力投影到六面体中心的径向轴上,由于dφ微小,故取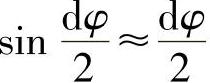 ,
,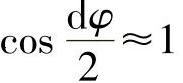 ,得平衡方程为
,得平衡方程为
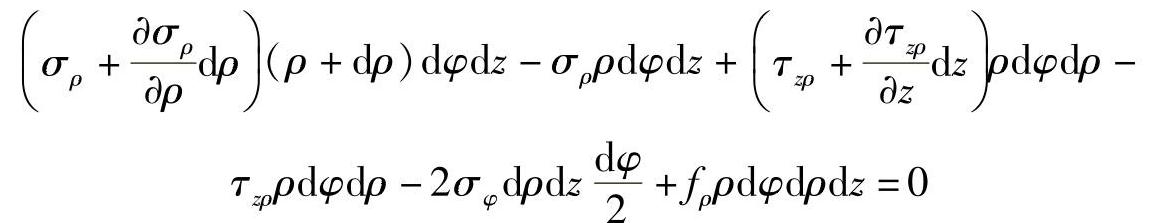
略去高阶项,整理得
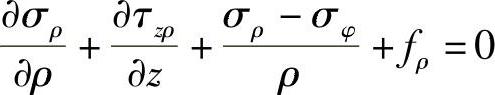
将六面体所受的各力投影到z轴上,得平衡方程
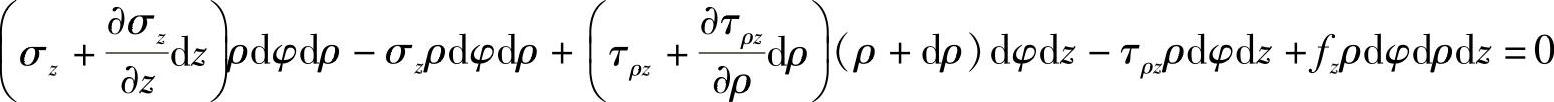
略去高阶项,整理得
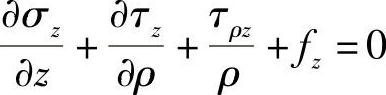
于是,得空间轴对称问题的平衡微分方程为
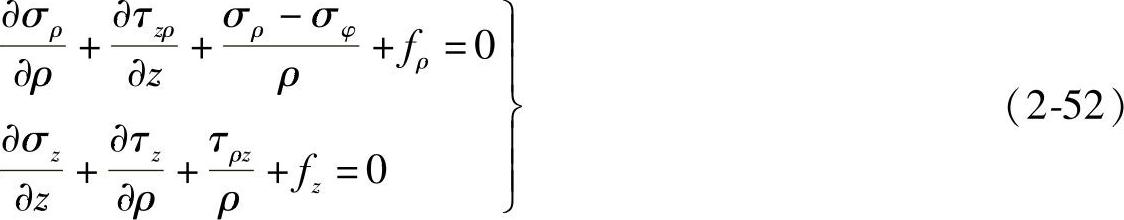
现在来导出轴对称问题的几何方程。
在极坐标中规定:ερ代表径向正应变;εφ代表环向线应变;εz代表轴向线应变;γzρ代表切应变(轴向与径向两线段之间的直角的改变);uρ代表径向位移;uz代表轴向位移。对称切应力γρφ、γφz及环向位移uφ都等于零。
通过与平面问题及极坐标中相同的分析,可见,由径向位移uρ引起的形变为
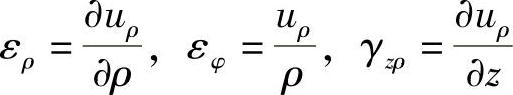
由径向位移uz引起的形变为
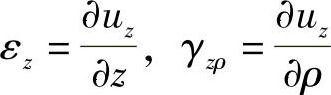
将以上两组形变进行叠加,得空间问题的几何方程为
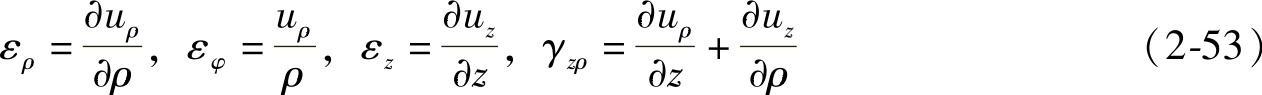 (www.daowen.com)
(www.daowen.com)
由于柱坐标和直角坐标同样也是正交坐标,所以物理方程的基本形式可以直接根据胡克定律得来
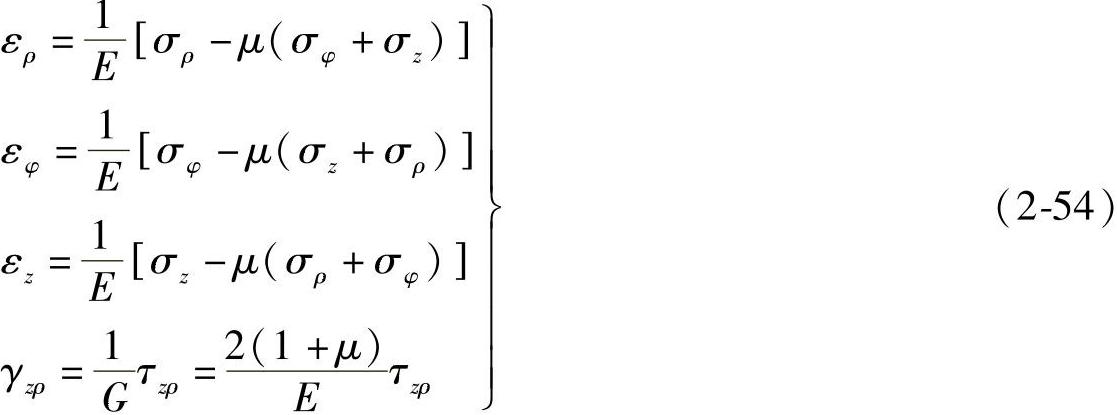
将式(2-54)中的前三式相加,仍然得到

其中的体应变为
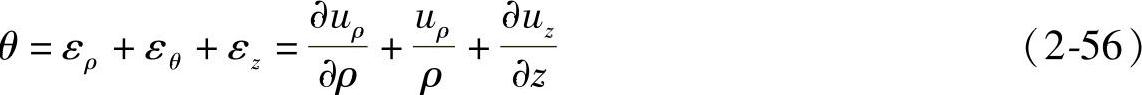
体积应力为
Θ=σρ+σθ+σz (2-57)
由式(2-54)中的第一式,可得
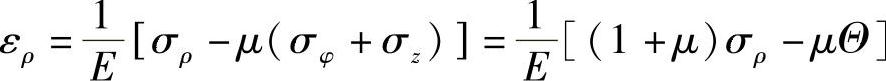
由上式解得σρ为
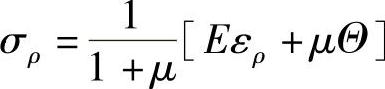
将式(2-55)得到的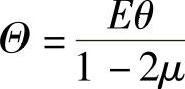 代入上式,得
代入上式,得
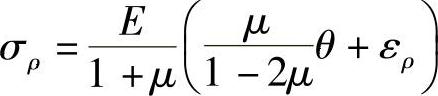
对于σφ和σz,也可以导出与此相似的两个方程。此外,再由式(2-54)求解切应力分量,总共得出如下的4个方程
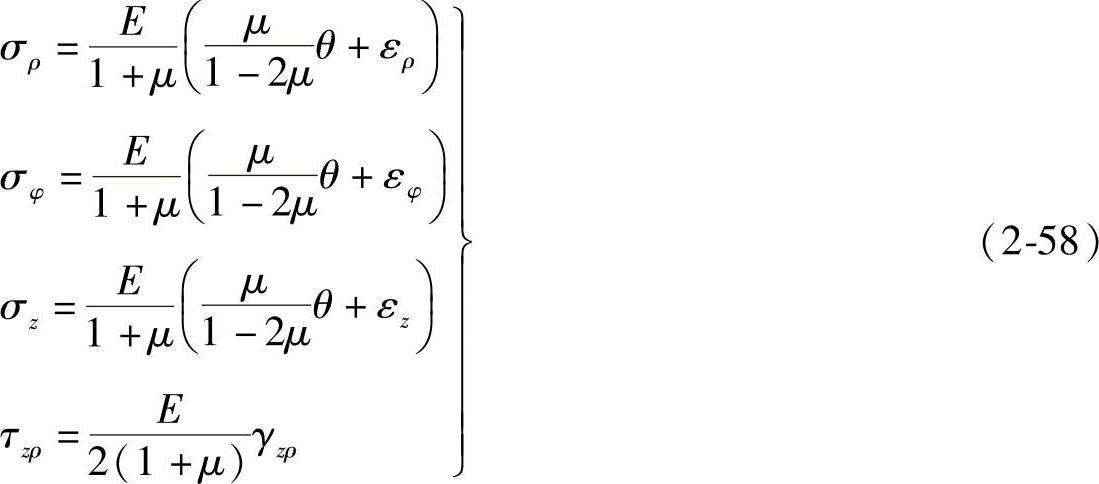
将几何方程(2-53)代入物理方程(2-58),得弹性方程为
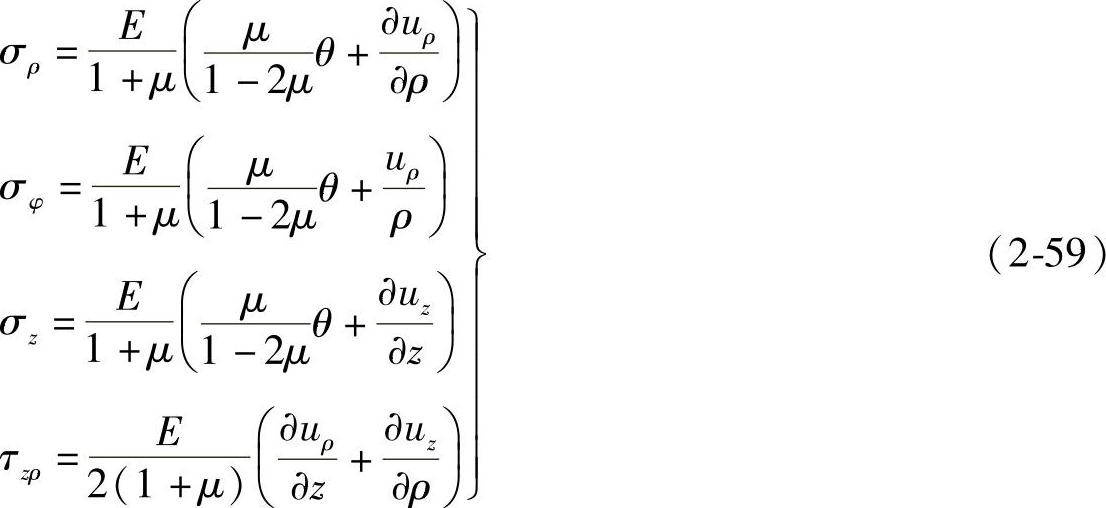
再将式(2-59)代入平衡微分方程(2-51),并采用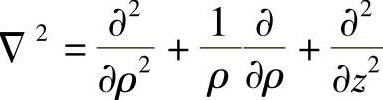 .得
.得
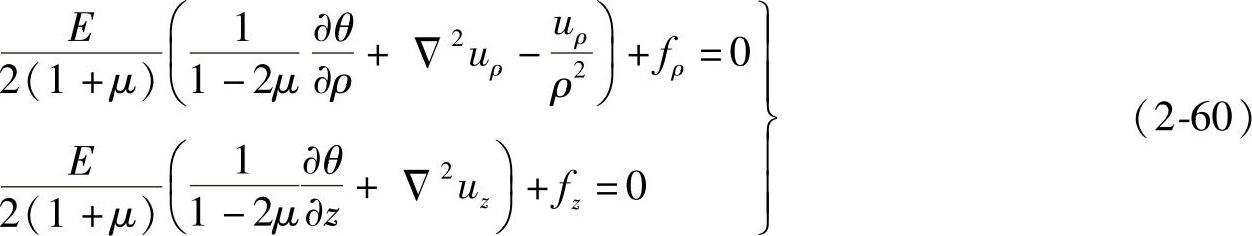
这是按照位移法求解空间轴对称问题时的基本微分方程。
此外,对于空间非轴对称问题,也可以采用柱坐标系进行分析和求解,在这里不在进行详细分析,仅给出在柱坐标系下空间非轴对称问题的平衡微分方程
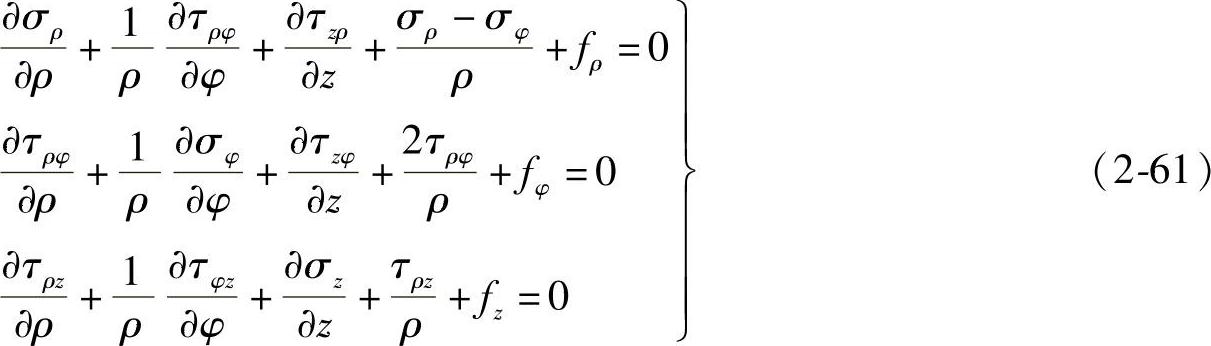
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







