在建立了弹性力学空间问题的基本方程和边界条件之后，像解决平面问题一样，也采用类似于代数方程中的消元法进行求解。下面分别对位移法和应力法进行介绍。

1.位移法

按位移求解问题，是取位移分量为基本未知函数，并要通过消元法，导出弹性体区域内求解位移的基本微分方程和相应的边界条件。对空间问题来说，这就要从15个基本方程中消去应力分量和形变分量，得出只包含3个位移分量的微分方程，推导如下。

将几何方程（2-40）代入物理方程（2-43），得出用位移分量表示的应力分量方程

式中，。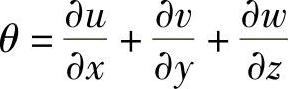

将式（2-46）代入平衡微分方程（2-35），并采用记号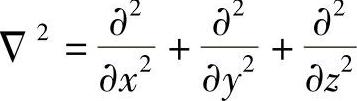，得到

这是用位移分量表示的应力平衡微分方程，也就是按位移求解空间问题时所需用的基本微分方程。

2.应力法

按应力求解问题，是取应力分量为基本未知函数，并要通过消元法，导出弹性体区域内求解应力的基本微分方程和相应的边界条件。对空间问题来说，这就要从15个基本方程中消去位移分量和形变分量，得出只包含6个应力分量的微分方程。因为平衡微分方程中本来就不包含位移分量和形变分量，所以只需从几何方程和物理方程中消去这些分量，推导如下。

首先从几何方程中消去位移分量，为此，将式（2-40）中第二式左边对z的二阶导数与第三式左边对y的二阶导数相加，得

由式（2-40）中的第四式可见，上式右边括弧内的表达式就是γ_yz，于是由上式及其余两个相似的方程式得

这是表明变形协调条件的一组方程，也就是一组所谓的相容方程。

将式（2-40）中的后三式分别对x，y和z求导，得(www.daowen.com)

并由此而得

于是由上式和其余两个相似的方程可得

这又是一组相容方程。

通过与上述相似的微分步骤，可以导出无数多的相容方程，都是形变分量所应当满足的。但是，可以证明，如果6个形变分量满足了相容方程[式（2-48）和式（2-49）]，就可以保证位移分量的存在，也就可以用几何方程（2-40）求得位移分量。

将物理方程（2-41）代入相容方程[式（2-48）和式（2-49）]，得出用应力分量表示的相容方程为

利用平衡微分方程（2-35），可以化简上式，使得每一式中包含体积应力和一个应力分量。当然，体力分量将在所有各式中出现。这样就得出米歇尔所推导的相容方程，即米歇尔相容方程

式中，。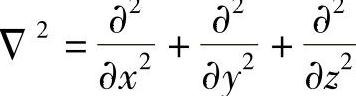

在体力分量为零或常量的情况下，式（2-50）可以简化为贝尔特拉米所推导的相容方程，即贝尔特拉米相容方程

按应力求解空间问题时，须使得6个应力分量在弹性体区域内满足平衡微分方程（2-35），满足相容方程[式（2-50）或式（2-51）]，并在边界上满足应力边界条件（2-45）。

由于位移边界条件难以用应力分量及其导数来表示，因此，位移边界问题和混合边界问题一般不能按应力求解而得到精确的函数式解答。

此外，按应力求解多连体问题时，仍然应考虑位移的单值条件。