在处理弹性力学问题时,选择什么形式的坐标系统,虽不会影响对问题本质的描绘,但却直接关系到解决问题的难易程度。如坐标选得合适,则可使问题大为简化。对于两类平面问题,均可根据所研究的弹性体的形状选取适当的坐标系进行求解。
1.平面问题的直角坐标系解答
由于偏微分方程[式(2-22)]的通解不能写成有限项的形式,因此一般不能直接求解问题,而只能采用逆解法或半逆解法。
逆解法:先设定某种形式的、满足相容方程[式(2-22)]的应力函数Φ,用式(2-21)求出应力分量,然后根据应力边界条件式(2-13)来考察,在各种形状的弹性体上,这些应力分量对应于什么样的面力,从而得知所设定的应力函数可以解决什么问题。
半逆解法:针对所要求解的问题,根据弹性体的边界形状和受力情况,假设部分和全部应力分量为某种形式的函数,从而推出应力函数Φ,然后来考察,这个应力函数是否满足相容方程,以及原来所假设的应力分量和由这个应力函数求出的其余应力分量,是否满足应力边界条件和位移单值条件。如果相容方程和各方面的条件都能满足,自然就得出正确的解答;如果某一方面不能满足,就要另作假设,重新考察。
下面举例说明逆解法的应用。
如图2-7所示,设有矩形截面的长梁(l远大于h),取单位厚度的梁来考察,并令每单位厚度上的力偶矩为M。
取Φ=ay3,不论系数a取何值,相容方程(2-22)总能满足。现在来考察,应力分量σx=6ay,σy=0,τxy=τyx=0能否满足边界条件,如果能满足,系数a该取何值。

图2-7 矩形截面的长梁
首先考虑上下两个主要边界(占边界绝大部分)的条件。在下边和上边,都没有面力,即要求
(σy)y=±h/2=0,(τyx)y=±h/2=0
这是能满足的,因为在所有各点都有σy=0,τyx=0。其次,考虑左右端次要边界(占边界很小部分)的条件。在左端和右端均没有铅垂力,即分别要求
(τxy)x=0=0,(τxy)x=l=0
这也是能满足的,因为在所有各点都有τxy=0。
此外,由于x=0,l的两端面是相对较小的边界,可以应用圣维南原理,将关于σx的边界条件改用主矢量和主矩的条件代替。即在左端和右端,边界面上σx合成的主矢量应为零,而σx合成的主矩应等于面力的力偶矩M,亦即

将σx=6ay代入,则上述两式化为
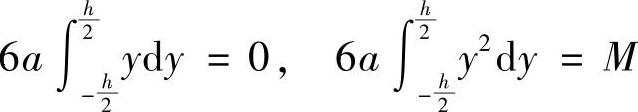
前一式总能满足,而后一式则要求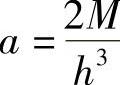 ,将其代入应力分量表达式,可得
,将其代入应力分量表达式,可得

由于梁截面的惯性矩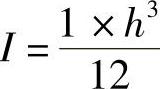 ,故上式又可以写为
,故上式又可以写为
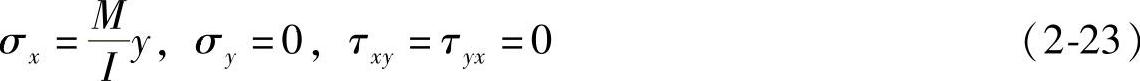
这就是矩形梁受纯弯曲时的应力分量,与材料力学中的完全相同。
假定这里是平面应力的情况,将应力分量(2-23)代入物理方程(2-10),得变形分量为
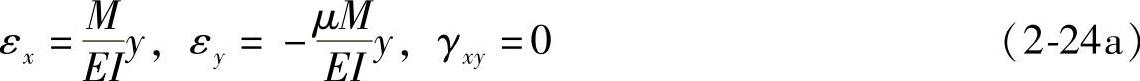
将式(2-24a)代入几何方程(2-7),可得
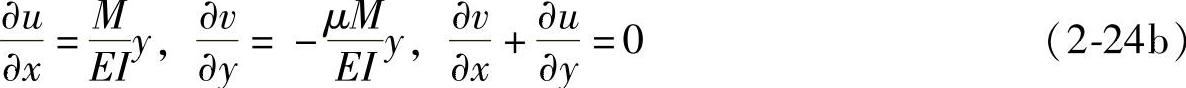
对式(2-24b)中前两式积分,可得
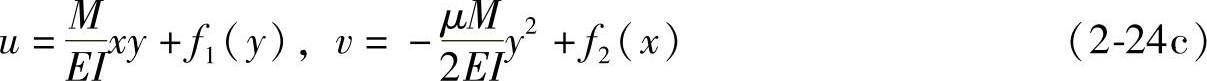
式中,f1(y)和f2(x)分别是y和x的待定函数。
将式(2-24c)代入式(2-24b)中的第三式,整理得

等式左边只是y的函数,而等式右边只是x的函数。因此,只可能两边都等于同一常数w。于是有
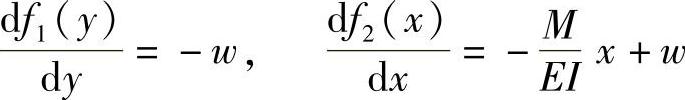
将上两式积分,可得
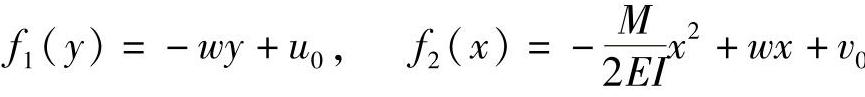
将上式代入式(2-24c),得位移分量为
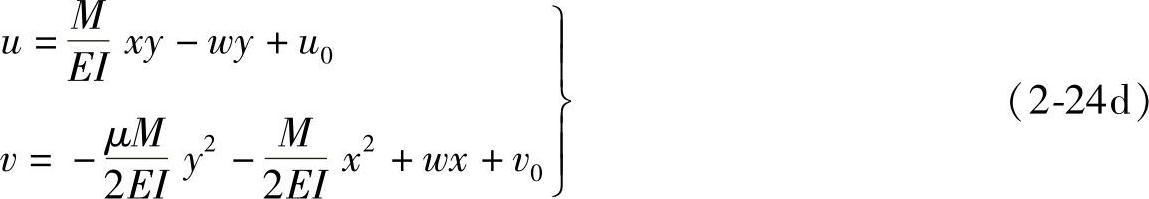
式中,任意常数w、u0及v0可由约束条件求得。由式(2-24d)可得梁的转角β和梁的各纵向曲面的曲率 为
为
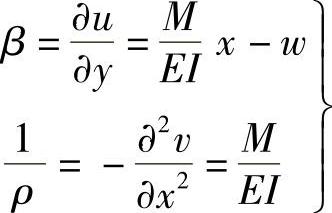
这是材料力学中的基本公式。
如果梁是悬臂梁,左端自由而右端完全固定,如图2-8所示,在梁的右端(x=l),对于y的任何值(-h/2≤y≤h/2),都要求u=0和v=0。在多项式解答中,这个条件是无法满足的。在实际工程上,这种完全固定的约束条件也是不大可能实现的。现在,和材料力学中一样,假定右端截面的中点不移动,则该点的水平线段不转动。这样,约束条件是
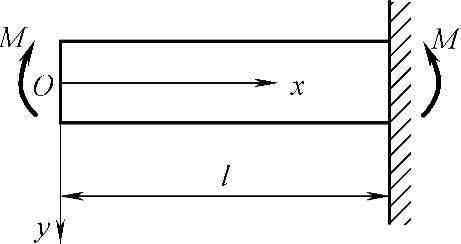
图2-8 悬臂梁受力情况

把上述约束条件代入式(2-24d),可确定常数w、u0及v0为
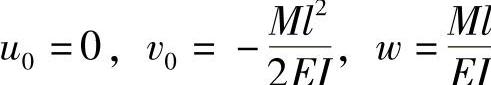
将求得的上述常数代入式(2-24d),可得出该悬臂梁的位移分量
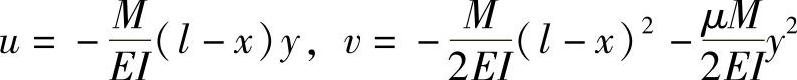
悬臂梁轴的挠度方程为
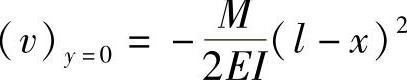
这与材料力学中的解答相同。
对于平面应变情况下的梁,须在以上的形变公式和位移公式中,将E换为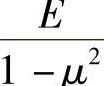 ,将μ换为
,将μ换为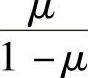 。
。
2.平面问题的极坐标系解答对于圆形、楔形、扇形等物体,采用极坐标求解比用直角坐标要方便得多。
(1)极坐标中平面问题的基本方程
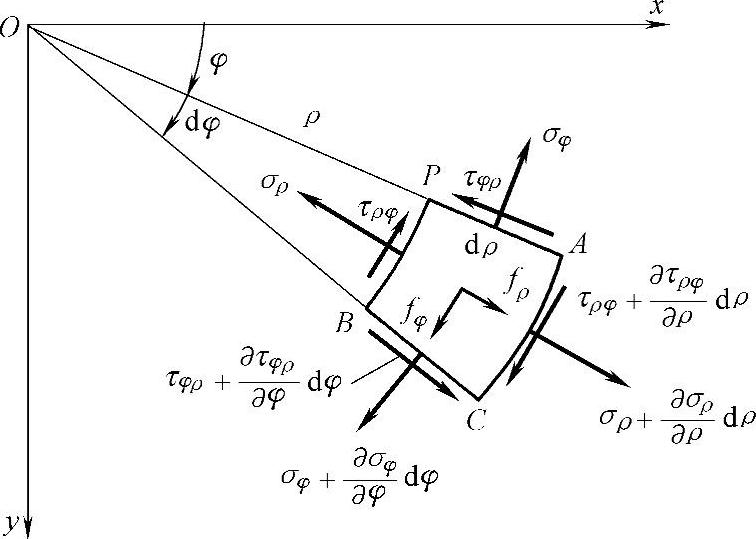
图2-9 极坐标下的微元体
1)极坐标中的平衡微分方程。如图2-9所示,考虑平面上的一个微元体PACB,沿ρ方向的正应力称为径向正应力,用σρ表示;沿φ方向的正应力称为环向正应力,用σφ表示;剪应力用τρφ及τφρ表示;径向及环向的体力分量分别用fρ及fφ表示。各量正负号的规定和直角坐标中一样。
与直角坐标系中相似,应力随坐标ρ的变化而变化,设PB面上的径向应力为σρ,则AC面上的应力将为 ,同样,这两个面上的切应力分别为τρφ和
,同样,这两个面上的切应力分别为τρφ和 。PA和BC两个面上的环向正应力分别为σφ及
。PA和BC两个面上的环向正应力分别为σφ及 ,这两个面上的切应力分别为τφρ及
,这两个面上的切应力分别为τφρ及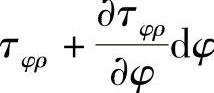 。
。
注意:两ρ面不平行,夹角为dφ;两ρ面面积不等,分别为ρdφ和(ρ+dρ)dφ;ρ从原点出发为正,φ从x轴向y轴方向转向为正;微分体的体积为ρdφdρ。
将微分体所受各力投影到微分体径向轴上,列出径向的平衡方程ΣFρ=0,得
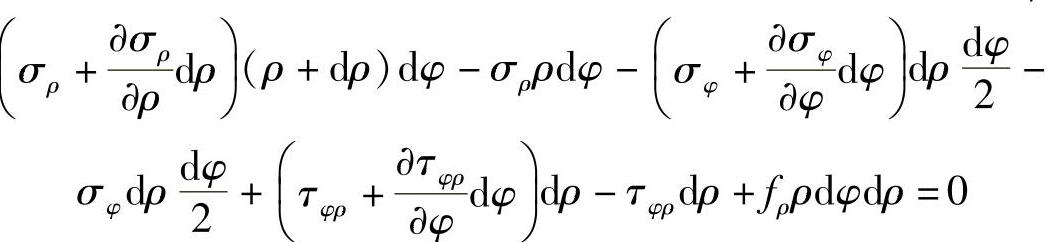
将微分体所受各力投影到微分体切向轴上,列出切向的平衡方程ΣFφ=0,得
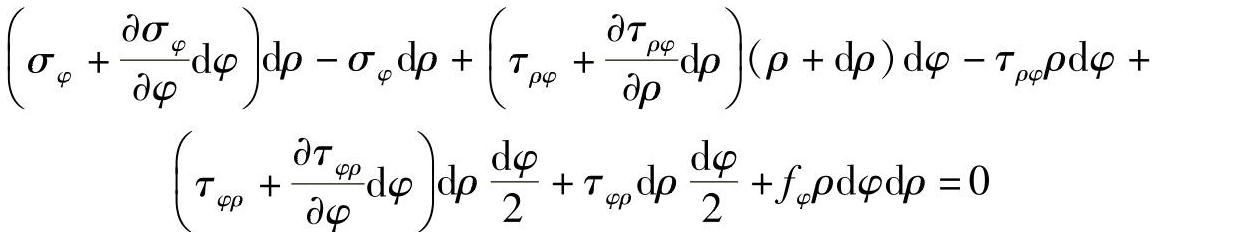
对于上述两个平衡方程式,由于dφ微小,故 ,用τρφ替代τφρ,略去高阶量,整理得
,用τρφ替代τφρ,略去高阶量,整理得
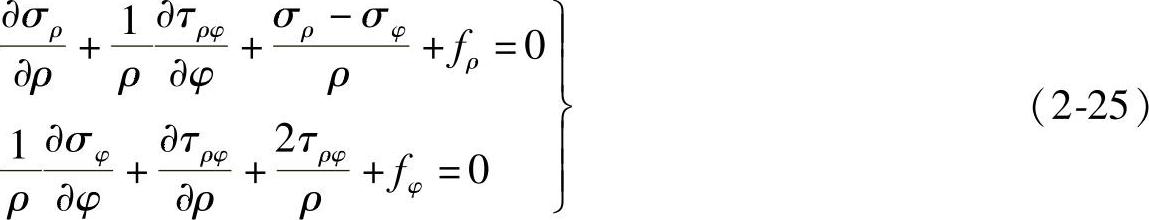
这就是极坐标中的平衡微分方程式。上述方程和直角坐标系下的平衡方程有所不同。在直角坐标系中,应力分量仅以偏导数的形式出现;在极坐标系中,则会由于微元体垂直于半径的两面面积不等而发生变化,而且半径越小差值越大。
2)极坐标中的几何方程。在极坐标中规定:ερ代表径向正应变;εφ环向线应变;γρφ代表切应变(径向与环向两线段之间的直角的改变);uρ代表径向位移;uφ代表环向位移。
如图2-10所示,通过任意一点P(ρ,φ),分别沿正方向做径向和环向的微分线段,PA=dρ,PB=ρdφ。现在来分析,微分线段上的形变分量和位移分量之间的几何关系。
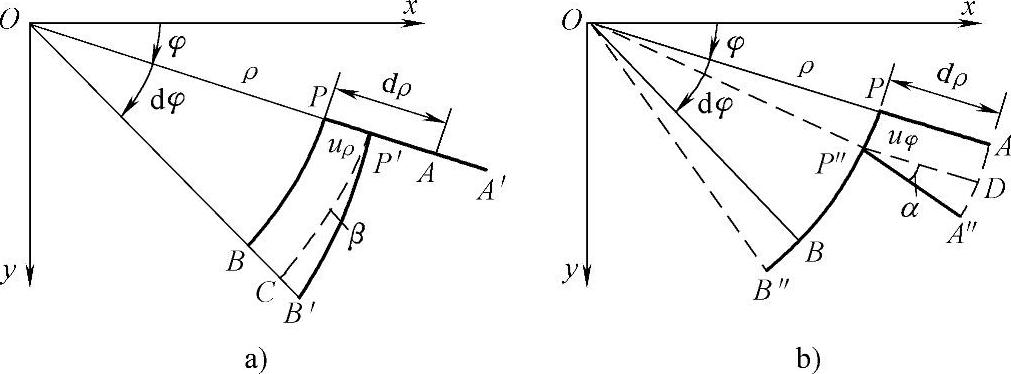
图2-10 极坐标下的几何关系
①假定只有径向位移,而无环向位移,如图2-10a所示。
由于发生假定的这个径向位移,径向线段PA移到P′A′,环向线段PB移到P′B′,而P、A、B三点的位移分别为

可见径向线段PA的线应变为(https://www.daowen.com)
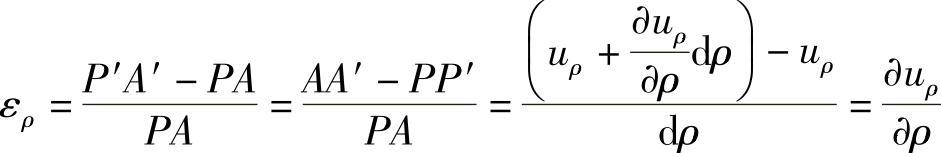
环向线段PB移到P′B′。在图2-10a中,通过点P′作圆弧线P′C。P′B′与P′C的夹角β是微小的,因此,P′B′≈P′C。由此可知,环向线段的线应变为

径向线段PA的转角为
α=0
环向线段PB的转角为
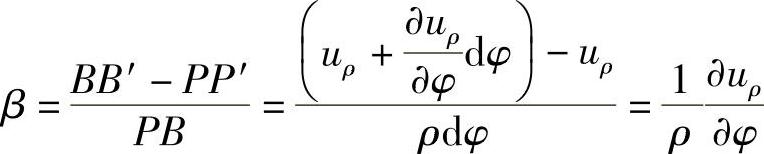
可见,切应变为
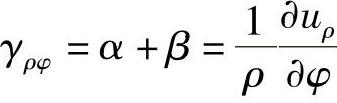
②假定只有环向位移,而无径向位移,如图2-10b所示。
由于发生假定的这个环向位移,径向线段PA移到P″A″,环向线段PB移到P″B″,而P、A、B三点的位移分别为
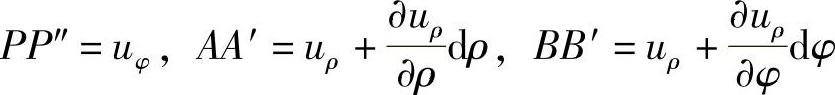
在图2-10b中,作P″D∥PA,则PA的转角为α。由于α是微小的,因此,略去高阶微量后可得到P″A″≈PA,由此得出径向线段PA的线应变ερ=0。
环向线段PB的线应变为
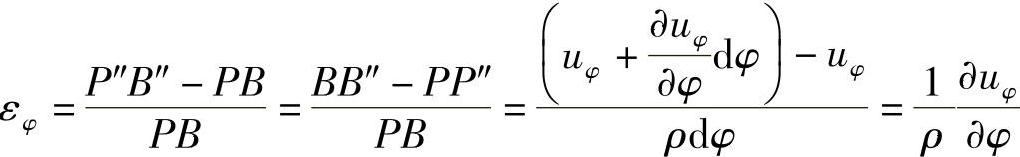
径向线段PA的转角为
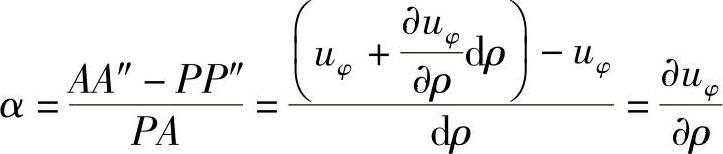
环向线段PB的转角(该转角使直角扩大)为
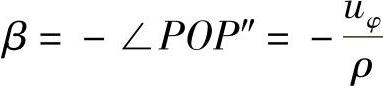
可见,切应变为
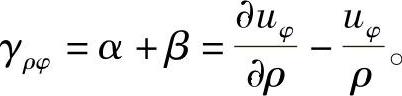
③沿径向和环向都有位移。
根据叠加原理,将①和②两种情况下相应的应变进行叠加,可得

这就是极坐标中的几何方程。
3)极坐标中的物理方程。下面来导出极坐标中平面向题的物理方程。在直角坐标中,物理方程是代数方程,且其坐标x和y的方向是正交的。在极坐标中,坐标ρ和φ的方向也是正交的,因此,极坐标系中的物理方程与直角坐标系中的物理方程具有同样的形式,只需将角码x和y分别改换为ρ和φ。据此,可得出极坐标系中平面应力问题的物理方程为

将式(2-27)中的E换为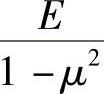 ,μ换为
,μ换为 ,可得到平面应变问题的物理方程为
,可得到平面应变问题的物理方程为
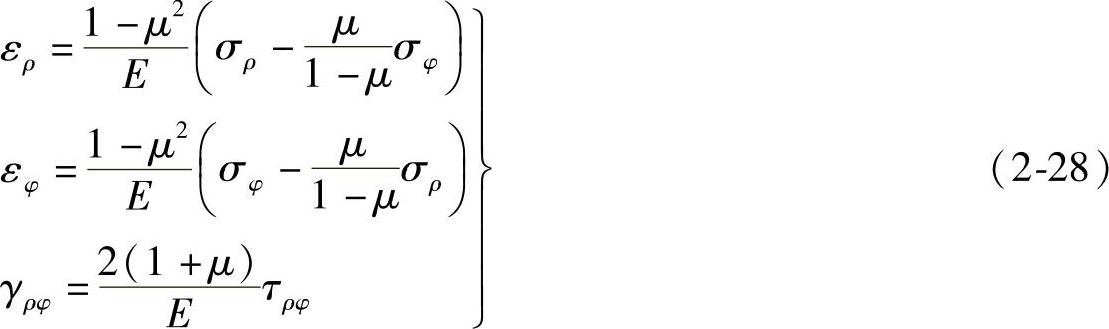
(2)极坐标中的相容方程与应力分量坐标变换 为了简化公式的推导,可以把直角坐标系中用应力函数表示的应力和相容方程直接变换到极坐标系中来。
1)极坐标中的相容方程。为了得到极坐标中用应力函数表示的应力和相容方程,可利用极坐标和直角坐标的关系:

x=ρcosφ,y=ρsinφ
由上述变换关系,可得ρ、φ对x、y的偏导数
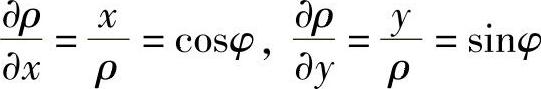

按照符合函数的求导公式,可得应力函数Φ的一阶导数的变换公式为
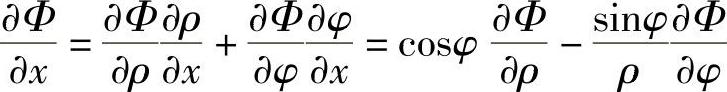
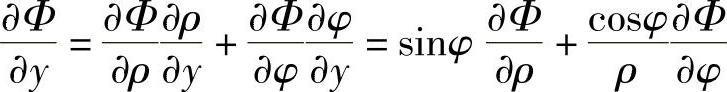
重复以上运算,得到应力函数Φ的二阶导数的变换公式为

由图2-9可知,如果把x轴和y轴分别转到ρ和φ的方向,使得微分体的φ坐标称为零,则σx、σy和τxy分别成为σρ、σφ和τρφ。于是不及体力时,由式(2-29)可得
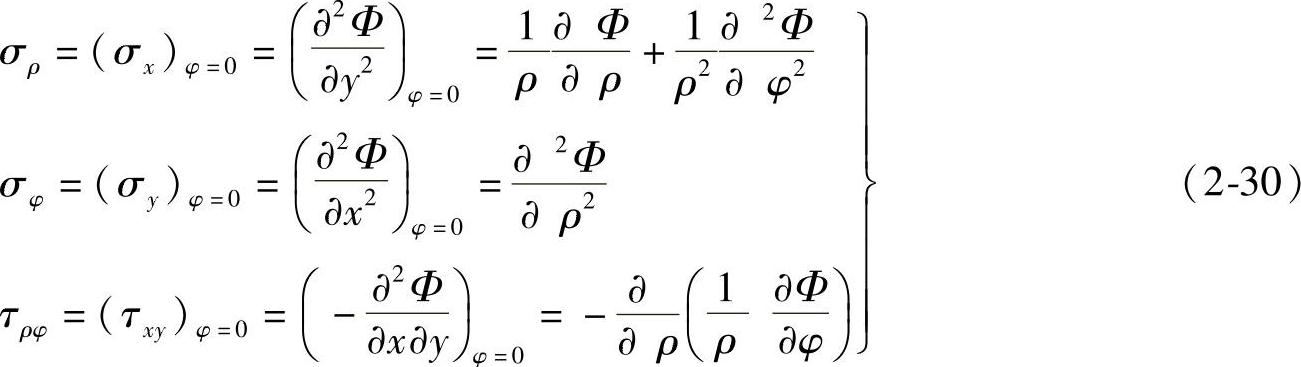
将式(2-29)中的前两式相加,可得

于是直角坐标系中的相容方程化为

用极坐标求解平面问题时(体力不计),就只需从相容方程[式(2-31)]求解应力函数Φ(x,y),然后由式(2-30)求出应力分量,再考察应力分量是否满足边界条件,多连体还要满足位移单值条件。
下面对轴对称情况下的相容方程作进一步说明。
对于轴对称问题应力数值轴对称,因此τρφ=τφρ=0,应力函数仅是ρ的函数,即Φ(ρ)。
在这一特殊情况下,式(2-30)可化为

相容方程(2-31)简化为
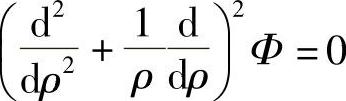
轴对称问题的拉普拉斯算子Δ 2可以写为
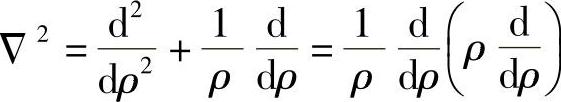
于是,轴对称问题的相容方程又可写为


图2-11 极坐标应力分量与直角坐标应力分量的关系
2)应力分量坐标变换。在一定的应力状态下,如果已知极坐标中的应力分量,就可以利用简单的关系式求得直角坐标中的应力分量。反之,如果已知直角坐标中的应力分量,也可以利用简单的关系式求得极坐标中的应力分量。因此,需要建立应力分量的坐标变化式。
设已知直角坐标系中的应力分量为σx、σy和τxy,试求极坐标中的应力分量σρ、σφ和τρφ。为此,在弹性体中取出一个包含x面和y面和ρ面且厚度为1的微小三角板A,如图2-11所示,其ab为x面,ac为y面,各面上的应力如图2-11所示。令bc边的长度为ds,则ab边及ac边的长度分别为dscosφ及dssinφ。
根据三角板A的平衡条件ᥐFρ=0,可以写出平衡方程
σρds-σxdscosφcosφ-σydssinφsinφ-τxydscosφsinφ-τyxdssinφcosφ=0
用τxy替代τyx,化简可得
σρ=σxcos2φ+σysin2φ+2τxysinφcosφ
同样,可由三角板A的平衡条件ΣFφ=0,得到
τρφ=(σy-σx)sinφcosφ+τxy(cos2φ-sin2φ)
类似地,在弹性体中取出一个包含x面、y面和φ面且厚度为1的微小三角板B,如图2-11所示。可由三角板B的平衡条件ᥐFφ=0,得到
σφ=σxsin2φ+σycos2φ-2τxysinφcosφ
并同样由平衡条件ΣFρ=0,得τφρ,且τφρ=τρφ。
综上可知,应力分量由直角坐标向极坐标的变换式为
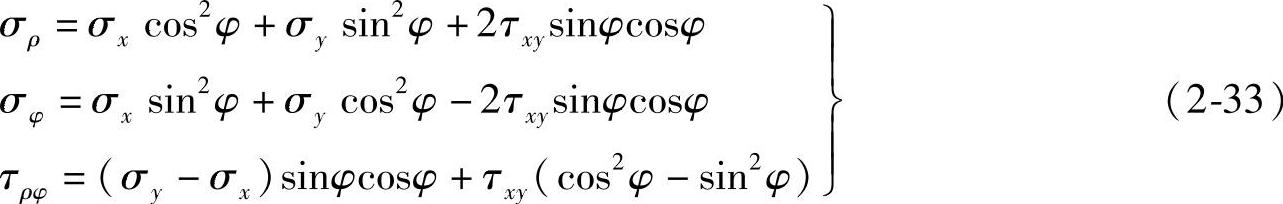
用类似的方法,导出的应力分量由极坐标向直角坐标的变换式为
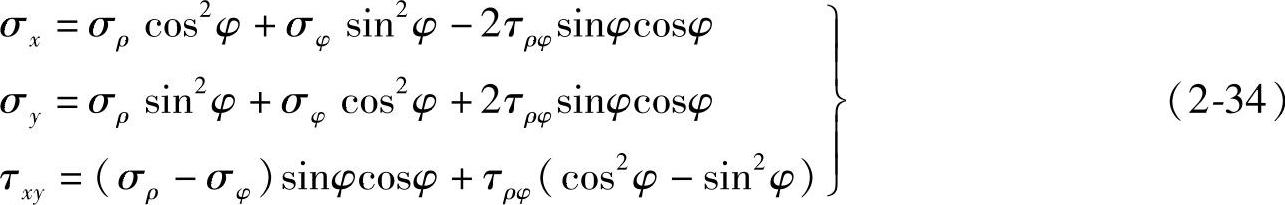
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







