在建立了弹性力学平面问题的基本方程和边界条件之后，通常采用类似于代数方程中的消元法进行求解。按位移求解的方法称为位移法，按应力求解的方法称为应力法。下面分别对两种方法进行介绍。

1.位移法

以u、v为基本未知函数，将平衡方程和边界条件都用u、v表示，并求出u、v，再由几何方程、物理方程求出应力与形变分量，此法即位移法。

现在来导出按位移法求解平面问题的方程和边界条件。为此，取位移分量u、v为基本未知函数。为了从方程和边界条件中消去形变分量和应力分量，须将它们用位移分量来表示。首先，几何方程（2-7）就是用位移分量表示形变分量的表达式。其次，对于平面应力问题，从物理方程（2-10）求出应力分量，使它们用形变分量表示。

再将几何方程（2-7）代入式（2-14），得

下面导出求解位移分量的方程和边界条件。将式（2-15）代入平衡微分方程式（2-1），可得

这就是按位移法求解平面应力问题时所用的基本微分方程。

另一方面，将式（2-15）代入应力边界条件（2-13），化简得

这就是用位移表示的应力边界条件。位移边界条件仍然如式（2-12）所示。

总之，按位移法求解平面应力问题时，要使得位移分量在区域内满足微分方程（2-16），并在边界上满足位移边界条件（2-12）或应力边界条件式（2-17）。

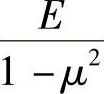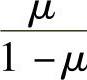平面应变问题与平面应力问题相比，除了物理方程不同以外，其他方程和边界条件都相同。只要将上述各方程和边界条件中的E换为，μ换为，就可得到平面应变问题按位移法求解的方程和边界条件。

2.应力法

以应力分量为基本未知函数，将所有方程都用应力分量表示，并求出应力分量，再由几何方程、物理方程求出形变分量与位移，此法即应力法。

现在来导出按应力法求解平面问题的方程。由于位移分量只存在几何方程中，可以先从几何方程中消去位移分量。考察几何方程式（2-7），即

将ε_x对y的二阶导数和ε_y对x的二阶导数相加，得(www.daowen.com)

即

该关系式称为变形协调方程或相容性方程。

现在，我们利用物理方程将相容性方程中的形变分量消去，使相容性方程中只包含应力分量。对于平面应力情况，将物理方程（2-10）代入式（2-18），得

利用平衡微分方程，化简上式，使它只包含正应力而不包含切应力，得

对于平面应变的情况，把_μ换为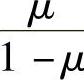，可得

总之，按应力法求解平面问题时，要使得应力分量在区域内满足微分方程式（2-1）及相容方程[式（2-19）或式（2-20）]，在边界上满足应力边界条件式（2-17），其中假设只求解全部为应力边界条件的问题。

对应力边界问题，且为单连体问题（只具有一个连续边界的物体），满足上述方程的解是唯一正确解。对多连体（具有多个连续边界的物体，也就是具有孔口的物体）问题，满足上述方程外，还需满足位移单值条件，才是唯一正确解。

常体力下，两种平面问题的相容方程都简化为

用记号Δ²代表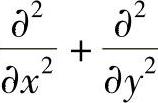，则上式化为

Δ²（σ_x+σ_y）=0

根据常体力下的平衡微分方程，推理可得

Φ称为平面问题的应力函数。将平面问题的相容方程用应力函数Φ表示，可得

按应力求解应力边界问题时，如果体力是常量，就只需由微分方程[式（2-22）]求解应力函数Φ，然后用式（2-21）求出应力分量，但这些应力分量在边界上应当满足应力边界条件。