1.平面问题的基本方程

在弹性力学中分析平面问题，要考虑静力学、几何学和物理学三方面的条件，分别建立三套方程。

（1）平衡微分方程及应力状态 考虑平面问题的静力学方面时，在弹性体内任一点取出一个微分体，根据平衡条件来导出应力分量和体力分量之间的关系式，也就是平面问题的平衡微分方程，并对物体内一点的应力状态进行分析。

从图2-4的薄板上取出一个微小的长方体，它在z方向的尺寸取为一个单位长度，在x方向和y方向上的长度分别为dx和dy。

设作用在单元体左侧面上的正应力是σ_x=σ_x（x，y），右侧面上坐标x得到增量dx，该面上的正应力为

σ_x（x+dx，y）

将上式展开为泰勒级数为

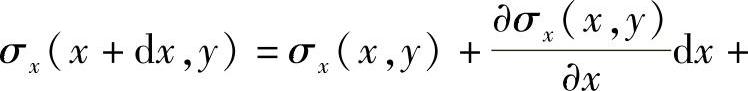
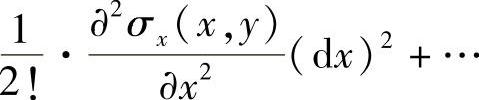
略去二阶及二阶以上的微量后便得

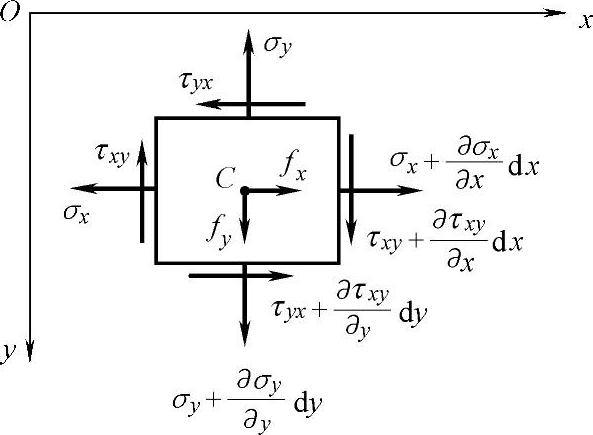
图2-4 单元体受力情况

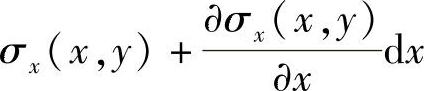
同理，σ_y、τ_xy、τ_yx一样处理。

根据力矩平衡条件，可得τ_xy=τ_yx。下面以y为投影轴，列出投影的力平衡方程

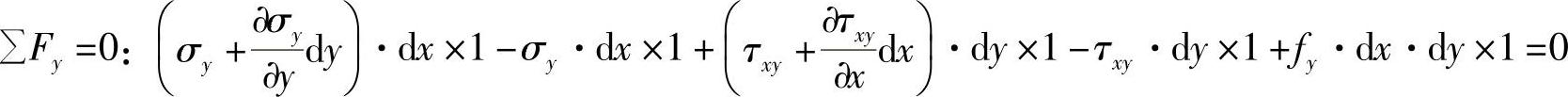
化简之后，两边除以dxdy，得

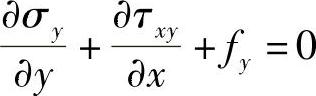
同理，以x投影轴可列出投影的力平衡方程ΣF_x=0。于是得出平面问题的平衡微分方程为

这两个微分方程对于两种平面问题都同样适用。

现在，我们继续研究平面问题的静力学方面，假定任一点P处坐标面上的应力分别为分量σ_x、σ_y和τ_xy=τ_yx，求经过该点任意斜截面上的应力，如图2-5a所示。为此在点P附近取一个平面AB，它平行于上述斜面，并与经过点P而垂直于x轴和y轴的两个平面画出一个微小的三角板或三棱柱PAB。当平面AB与P点无限接近时，平面AB上的平均应力就成为上述斜截面上的应力，如图2-5b所示。

用n代表斜面AB的外法线方向，其方向余弦为cos（n，x）=l，cos（n，y）=m；并用p_x和p_y分别代表斜面AB上的全应力p在x轴及y轴上的投影。设斜面AB的长度为ds，则PB面及PA面的长度分别为lds和mds，PAB的面积为ldsmds/2。垂直于图平面的尺寸取为1。由平衡条件ΣF_x=0，可得

p_xds-σ_xlds-τ_yxmds+f_xldsmds/2=0

式中，f_x为x方向的体力分量。将上式化简可得

p_x=lσ_x+mτ_yx

同理，由平衡条件ΣF_y=0，可得

即

设斜面AB上的正应力为σ_n，则由p_x和p_y的投影，可得σ_n=lp_x+mp_y，把式（2-2）代入，可得

σ_n=l²σ_x+m²σ_y+2lmτ_xy （2-3）

同理，可得切应力为

τ_n=lp_y-mp_x=lm（σ_y-σ_x）+（l²-m²）τ_xy （2-4）

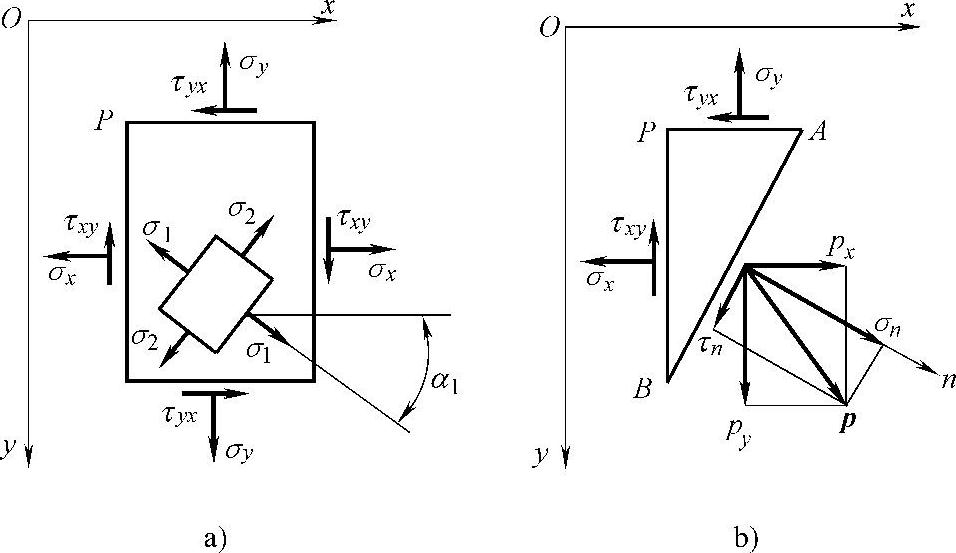
图2-5 平面受力情况

设经过点P的某一斜面上的切应力等于零，则该斜面上的正应力称为点P的一个主应力，而该斜面称为点P的一个应力主面，该斜面的法线方向（即主应力的方向）称为在点P的一个应力主向。

在一个应力主面上，由于切应力等于零，全应力就等于该面上的正应力，也就等于主应力σ，因此，该面上的全应力在坐标轴上的投影为

p_x=lσ，p_y=mσ

将其带入式（2-2），可得

lσ=lσ_x+mτ_yx，mσ=mσ_y+lτ_xy

由上两式，可得σ²-（σ_x+σ_y）σ+（σ_xσ_y-τ²_xy）=0，从而求得两个主应力为

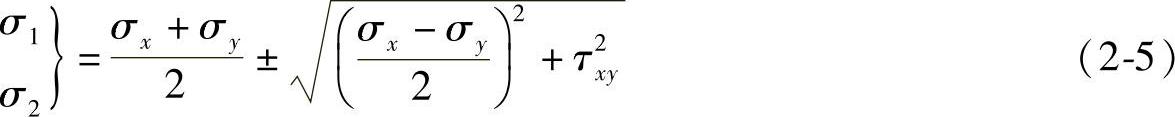
由式（2-5），可得

σ_x+σ_y=σ₁+σ₂ （2-6）

可以证明，两个主应力方向相互垂直，其中一个为最大正应力，另一个为最小正应力；最大与最小的切应力为±（σ₁-σ₂）/2，且发生在与主应力呈45°的斜面上。(www.daowen.com)

（2）几何方程 仅靠平面问题的平衡微分方程还不能解决问题，还必须考虑几何学和物理学方面的条件。下面根据几何学，导出微分线段上的形变分量与位移分量之间的关系式，也就是平面问题的几何方程。

经过弹性体内的任意一点P，沿x轴和y轴的正方向取两个为微小长度的线段PA=dx，PB=dy，如图2-6所示。假定弹性体受力以后，P、A、B三点分别移动到P′、A′、B′。

首先来求线段PA和PB的线应变，即ε_x和ε_y，用位移分量来表示。设点P在x方向的位移为u，则A点在x方向的位移，由于x坐标的改变，将是

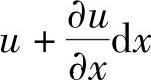。于是，线段PA的线应变为

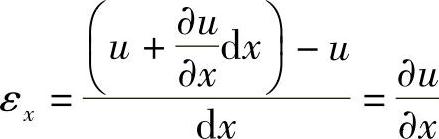
同理，线段PB的线应变为。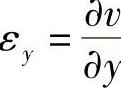

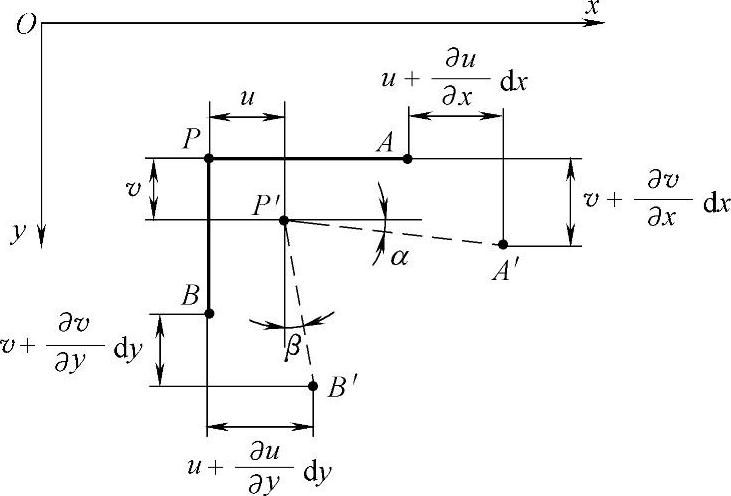
图2-6 弹性体的几何关系

现在求出线段PA和PB之间夹角的改变，也就是切应变γ_xy，用位移分量表示。由图2-6可见，这个切应变是由两部分组成的：一部分是由y方向的位移v引起的，即x方向的线段PA的转角α；另一部分是由y方向的位移u引起的，即y方向的线段PB的转角β。

设点P在y方向的位移为v，则A点在y方向的位移，由于x坐标的改变，将是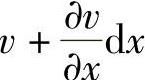。于是，线段PA的转角为

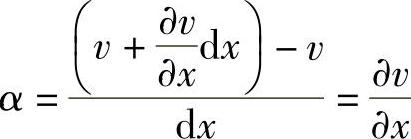
同理，线段PB的转角为。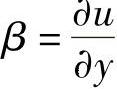

可见，线段PA和PB之间夹角的改变（以减小时为正），也就是切应变γ_xy可表示为

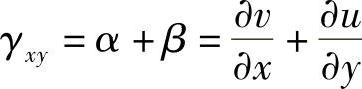
因此，平面问题的几何方程为

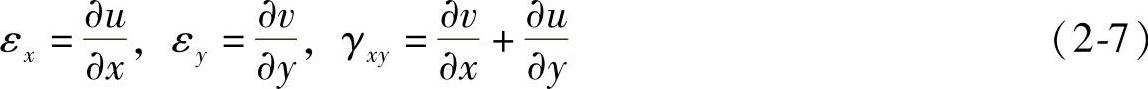
与平衡微分方程一样，上述几何方程对两种平面问题都适用。由几何方程可见，当物体的位移分量完全确定时，形变分量即完全确定；然而，当形变分量完全确定时，位移分量却不能完全确定。

（3）物理方程 现在来考虑平面问题的物理学方面，导出形变分量与应力分量之间的关系式，也就是平面问题的物理方程。

在理想弹性体中，形变分量与应力分量之间的关系极其简单，已在材料力学中根据胡克定律导出为

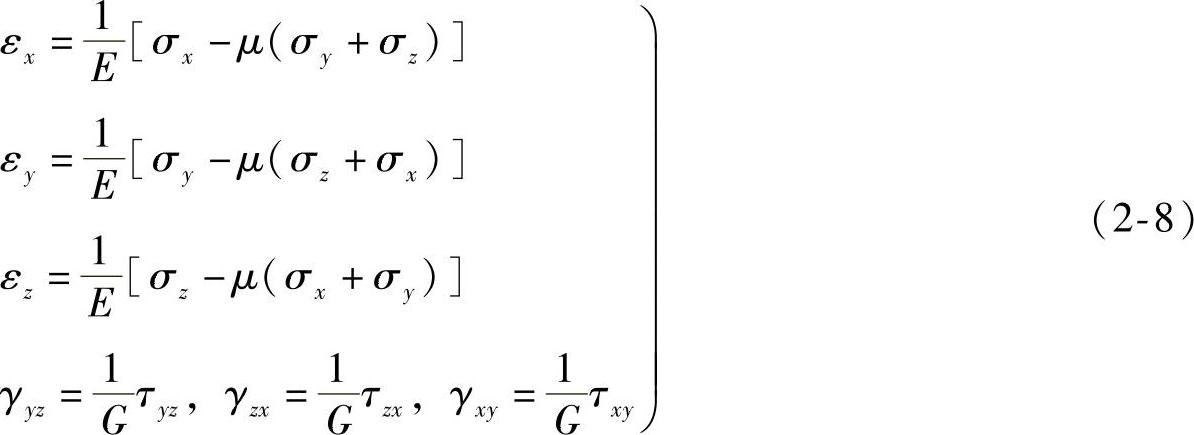
式中，E为弹性模量；G为剪切模量；μ为泊松比。这三个常数之间的关系为

在平面应力问题中，σ_z=0，将其及式（2-9）代入式（2-8），可得

这就是平面应力问题的物理方程。此外，式（2-8）中的第三式变为

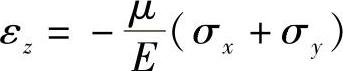
由上式可知，ε_z可由σ_x和σ_y得出，因而不作为独立的未知函数，并由ε_z可以求出薄板厚度的改变。又由式（2-8）中的第四式及第五式可知，因为在平面问题中有τ_yz=0和τ_zx=0，所以有γ_yz=0和γ_zx=0。

在平面应变问题中，因为物体的所有点都不沿z方向移动，所以z方向的线段都没有伸缩，即ε_z=0。于是，由式（2-8）中的第三式，可得

σ_z=μ（σ_x+σ_y）

同样，σ_z也不作为独立的未知函数。将上式代入式（2-8）中的第一式及第二式，并结合第三式，得

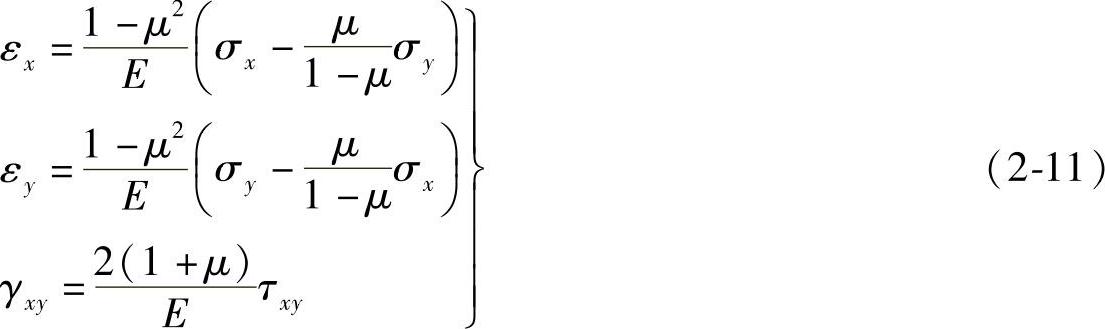
这就是平面应变问题的物理方程。此外，因为在平面应变问题中也有τ_yz=0和τ_zx=0，所以也有γ_yz=0和γ_zx=0。

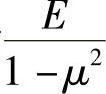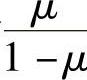可以看出，两种平面问题的物理方程是不一样的。然而，如果在平面应力的物理方程[式（2-10）]中，将E换为，μ换为，就得到平面应变问题的物理方程[式（2-11）]。

以上导出的三套方程，就是弹性力学平面问题的基本方程：2个平衡微分方程[式（2-1）]，3个几何方程[式（2-7）]，3个物理方程[式（2-10）或式（2-11）]。这8个基本方程中包含8个未知数。此外，必须考虑弹性体边界条件，才有可能求出这些未知函数。

2.平面问题的边界条件

当物体处于平衡状态时，其内部各点的应力状态应满足平衡微分方程，在边界上应满足边界条件。按照边界条件的不同，弹性力学问题分为位移边界问题、应力边界问题和混合边界问题。

（1）位移边界条件 当边界上已知位移时，应建立物体边界上点的位移与给定位移相等的条件。如令给定位移的边界为S_u，则有（在S_u上）

式中，（u）s和（v）s表示位移的边界值，而u和v在边界上是坐标的已知函数。

（2）应力边界条件 当物体的边界上给定面力时，则物体边界上的应力应满足与面力相平衡的平衡条件。例如，在Sσ部分边界上给定了面力分量f_x（s）和f_y（s），则可以由边界上任意一点微分体的平衡条件，导出应力与面力之间的关系。为此，在边界上任意一点P取出一个类似于图2-5的微分体。这时，斜面AB就是变截面，在此面上的应力分量p_x和p_y应代换为面力分量f_x和f_y，而坐标面上的σ_x、σ_y和τ_xy则分别称为应力分量的边界值。由平衡条件得出平面问题的应力边界条件（在Sσ上）为

式中，f_x（s）和f_y（s）在边界上是坐标的已知函数；l和m是边界面外法线的方向余弦。

（3）混合边界条件 物体的一部分边界上具有已知位移，因而具有位移边界条件，如式（2-12）所示；另一部分边界上则具有已知面力，因而具有应力边界条件，如式（2-13）所示。即两部分边界上分别有应力边界条件和位移边界条件。此外，在同一部分边界上还可能出现混合边界条件，即两个边界条件中的一个是位移边界条件，另一个是应力边界条件。

需要指出的是，在求解弹性力学问题时，应力分量、形变分量和位移分量等必须满足区域内的三套基本方程，还必须满足边界条件，因此，弹性力学问题属于数学物理方程中的边值问题。但是，要使边界条件得到完全满足，往往会遇到很大的困难。这时，我们可以利用圣维南原理局部边界条件进行简化。