弹性力学中经常用到的基本概念包括外力、内力、形变和位移。下面对这些概念加以详细说明。

作用于物体的外力分为体积力和表面力，也分别简称为体力和面力。

所谓体力，是分布在物体体积内的力，例如重力和惯性力。物体内各点受体力的情况一般是不相同的。为了表明该物体在某一点P所受体力的大小和方向，在这一点取物体的一小部分，它包含着点P，而它的体积为ΔV，如图2-1a所示。设作用于ΔV的体力为ΔF，则体力的平均集度为ΔF/ΔV。如果把所取的那一小部分物体不断减小，即ΔV不断减小，则ΔF和ΔF/ΔV都将不断地改变大小、方向和作用点。现在，令ΔV无限减小而趋于点P，假定体力为连续分布，则ΔF/ΔV将趋于一定的极限f，即

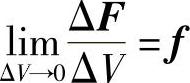
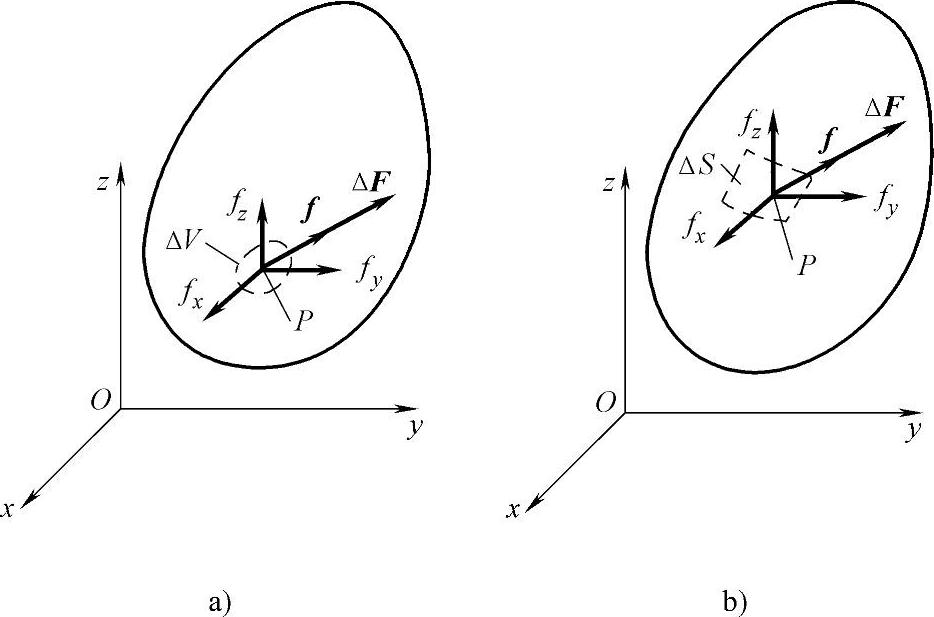
图2-1 体力和面力

这个极限矢量限f就是该物体在点P所受体力的集度。因为ΔV是标量，所以f的方向就是ΔF的方向。矢量f在坐标轴x、y、z上的投影f_x、f_y、f_z，成为该物体在点P的体力分量，以沿坐标轴正方向为正，沿坐标轴负方向为负，其量纲是L^-2MT^-2。

所谓面力，是分布在物体表面上的力。物体在其表面上各点受面力的情况一般也是不同的。为了表明该物体在表面上某一点P所受面力的大小和方向，在这一点取该物体表面的一小部分，它包含点P且面积为ΔS，如图2-1b所示。设作用于ΔS的面力为ΔF，则面力的平均集度为ΔF/ΔS。与上述相似，令ΔS无限减小而趋于点P，假定面力为连续分布，则ΔF/ΔS将趋于一定的极限f，即

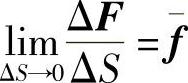
这个极限矢量f就是该物体在点P所受面力的集度。因为ΔS是标量，所以f的方向就是ΔF的方向。矢量f在坐标轴x、y、z上的投影f_x、f_y、f_z，成为该物体在点P的面力分量，以沿坐标轴正方向为正，沿坐标轴负方向为负，其量纲是L^-1MT^-2。

物体受外力以后，其内部将产生内力，即物体本身不同部分相互作用的力。为了研究物体在其某一点P处的内力，假想用经过点P的一个截面mn将该物体分为Ⅰ和Ⅱ两部分，而将Ⅱ部分撇开，如图2-2所示，撇开的部分Ⅱ将在截面mn上对留下的部分Ⅰ作用一定的内力。取这一截面的一小部分，它包含点P且面积为ΔA，设作用于ΔA上的面力为ΔF，则内力的平均集度，即平均应力为ΔF/ΔA。令ΔA无限减小而趋于点P，假定内力为连续分布，则ΔF/ΔA将趋于一定的极限p，即

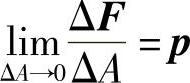
这个极限矢量p就是该物体在截面mn上点P处的应力。因为ΔA是标量，所以p的方向就是ΔF的极限方向。它与物体的形变和材料强度是直接相关的，应力在其作用截面的法线方向及切线方向的分量，也就是正应力σ和切应力τ，如图2-2所示。应力及其分量的量纲是L^-1MT^-2。(www.daowen.com)

显然，在物体内的同一点P，不同截面上的应力是不同的。为了分析这一点的应力状态，即各个截面上应力的大小和方向，在这一点从物体内取出一个微小的正六面体，它的棱边分别平行于三个坐标轴且长度为PA=Δx，PB=Δy，PC=Δz，如图2-3所示。

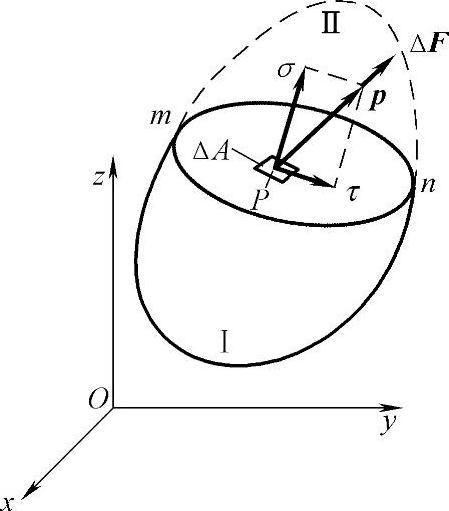
图2-2 P点处的应力

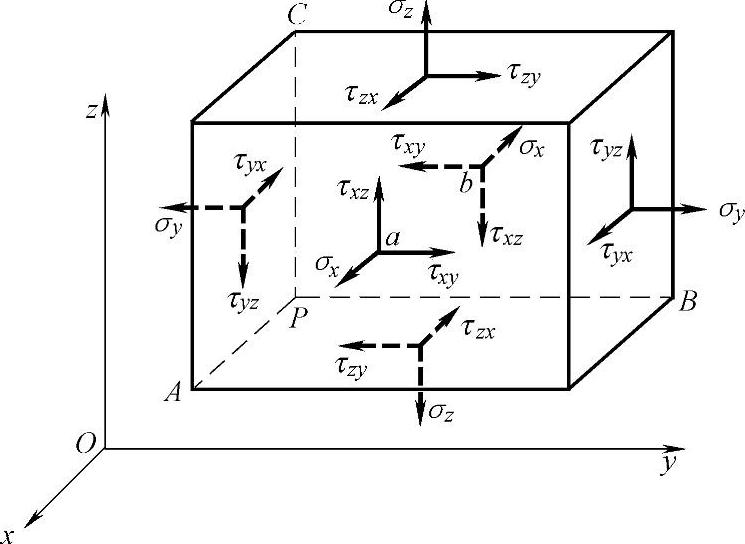
图2-3 正平行六面体的应力状态

将每一面上的应力分解为一个正应力和切应力，分别与三个坐标轴平行。正应力用σ表示。为了表明这个正应力的作用面和作用方向，加上一个下标字母。例如，正应力σ_x是作用在垂直于x轴的面上，同时也是沿着x轴的方向作用的。切应力用τ表示，并加上两个下标字母，前一个字母表示作用面垂直于哪一个坐标轴，后一个字母表示作用方向沿着哪一个坐标轴。例如，切应力τ_xy是作用在垂直于x轴的面上且沿着y轴方向作用的。

如果某一个截面上的外法线是沿着坐标轴的正力向，这个截面就称为一个正面，这个面上的应力就以沿坐标轴正方向为正，沿坐标轴负方向为负。相反，如果某一个截面上的外法线是沿着坐标轴的负方向，则这个截面就称为一个负面，这个面上的应力就以沿坐标轴负方向为正，沿坐标轴正方向为负。图2-3上所示的应力全都是正的。根据力矩平衡方程，可得六个切应力之间的关系：τ_xy=τ_yx，τ_zy=τ_yz，τ_xz=τ_zx。这就是切应力互等定理：作用在两个互相垂直的面上并且垂直于该面交线的切应力是互等的（大小相等，符号相同）。在物体的任意一点，如果已知σ_x、σ_y、σ_z、τ_yz、τ_zx和τ_xy这六个应力分量，就可以求得经过该点的任意截面上的正应力和切应力。因此，上述六个应力分量可以完全确定该点的应力状态。

所谓形变，就是形状的改变。物体的形状总可以用它各部分的长度和角度来表示。因此，物体的形变总可以归结为长度和角度的改变。

为了分析物体在某一点P的变形状态，在这一点沿着坐标轴x、y、z的正方向取三个微线段PA、PB、PC。物体变形之后，这三个线段的长度以及它们之间的夹角一般都将有所改变。各线段的每单位长度的伸缩，称为线应变，亦称正应变；各线段之间的夹角的改变，用弧度表示，称为角应变。线应变用字母ε表示，如ε_x表示x方向的线段PA的线应变。

线应变以伸长时为正，缩短时为负，与正应力的正负号规定相适应。切应变用字母γ表示：如γ_xy表示x和y两方向的线段（PA与PB）之间夹角的改变。切应变以夹角变小时为正，变大时为负，与切应力的正负号规定相适应。在物体的任意一点，如果已知ε_x、ε_y、ε_z、γ_yz、γzx和γxy这六个应力分量，就可以求得经过该点的任意线段的线应变，也可以求得经过该点的任意线段之间的角度的改变。因此，上述六个应变，称为该点的形变分量，可以完全确定该点的形变状态。

所谓位移，就是位置移动。物体内任意一点的位移，用它在x、y、z三轴上的投影u、v、w来表示，以沿坐标轴正方向为正，沿坐标轴负方向为负。这三个投影称为该点的位移分量。位移及其分量的量纲是L。

一般而论，弹性体内任意一点的体力分量、面力分量、应力分量、形变分量和位移分量，都是随着该点的位置而变的，因而都是位置坐标的函数。