1.点的三面投影及其规律
点、线、面是构成空间形体的基本几何元素,它们是不能脱离形体而孤立存在的,研究空间形体的投影规律,必须从点、线、面着手,掌握了这些基本几何元素的投影规律,无论多么复杂的形体也就变得非常简单了。而点的投影是最简单、最基本的。
如图1-12a所示,将空间点A置于第一投影区,过A点分别作H面、V面、W面的垂直线(投射线⊥投影面),并分别与H面、V面、W面相交于a、a′、a″,a、a′、a″即为A点的H面投影、V面投影和W面投影。
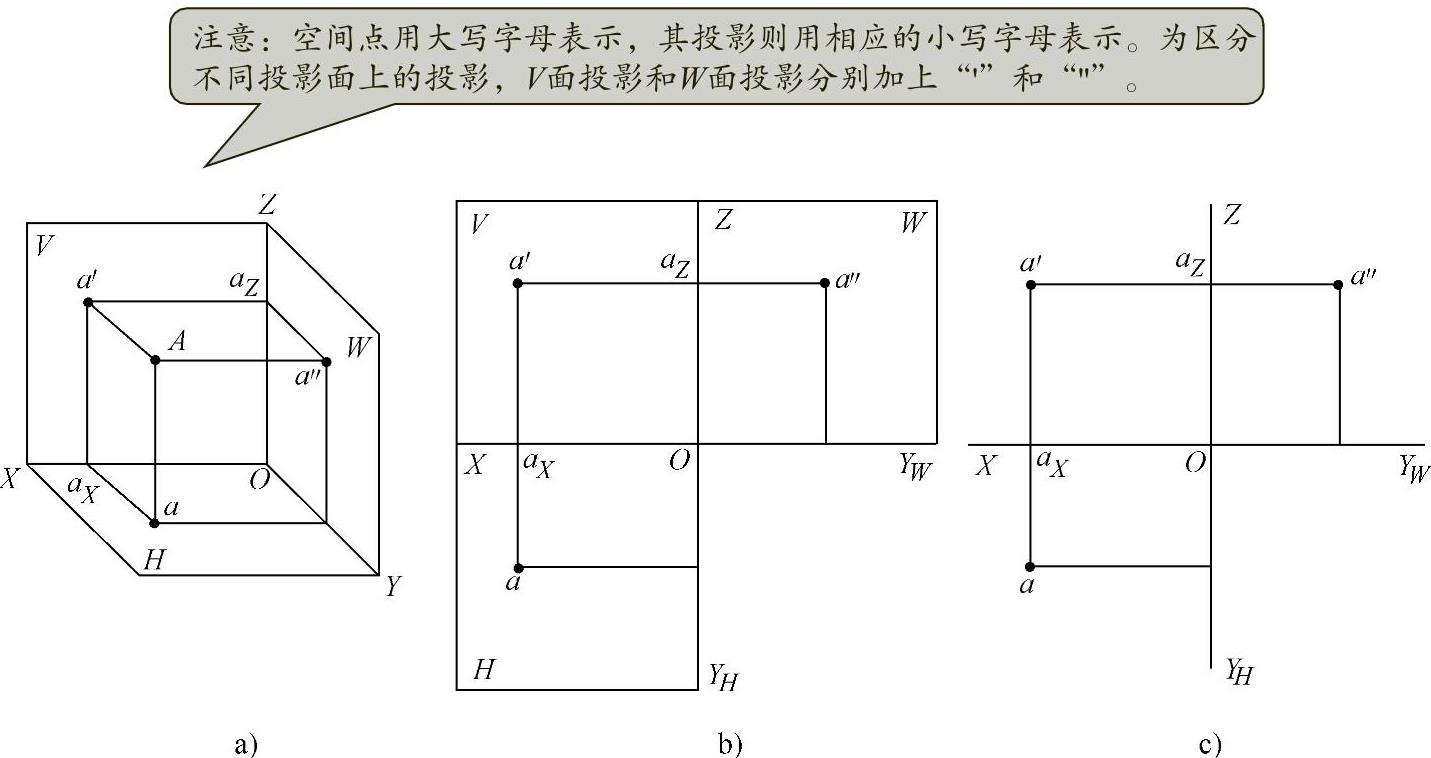
图1-12 点的三面投影
a)轴测图 b)展开图 c)正投影画法
将A点的三面投影展开,即得到A点的三面投影图,如图1-12b所示。H面与V面的交线为投影轴OX,V面与W面的交线为投影轴OZ,而H面与W面的交线,即投影轴OY被分成了两根,留在H面上的记作OYH,留在W面上的记作OYW。为了简化图面,通常投影面的边框和投影面的名称均省略标注,如图1-12c所示。
在图1-12中,Aa⊥H面,Aa′⊥V面,则Aa⊥OX,Aa′⊥OX,所以OX垂直于Aa与Aa′所确定的平面,则OX⊥aaX,OX⊥a′aX,因而a′a⊥OX,交OX于aX。同理,a′a″⊥OZ,交OZ于aZ。事实上,可以将A点看成一个长方体的顶点,AaX、AaY、AaZ是长方体的三个表面,另外三个表面分别位于三个投影面上,那么aaX=a″aZ,是A点到V面的距离。
由此,可以总结出点的正投影规律:
1)点的正面投影与水平投影的连线垂直于OX轴,即a′a⊥OX。
2)点的正面投影与侧面投影的连线垂直于OZ轴,即a′a″⊥OZ。
3)点的水平投影到OX轴的距离等于点的侧面投影到OZ轴的距离,即aaX=a″aZ。
根据以上投影规律,如果知道点的任意两面投影,就可以求出另外一面投影。
例1-1 已知点的正面投影a′与水平投影a,求侧面投影a″,如图1-13a所示。
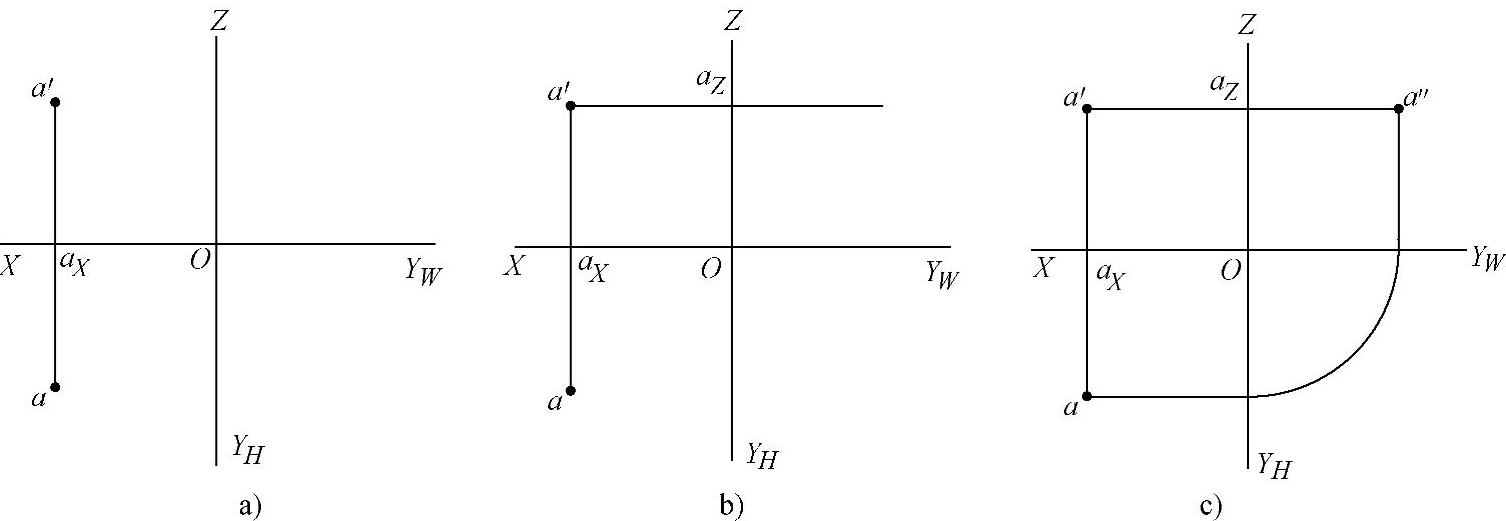
图1-13 根据点的正面和水平投影求侧面投影
解:1)过a′引水平线,根据点的正投影规律,点的侧面投影a″必定在此水平线,如图1-13b所示;
2)连接a′a;
3)量取水平投影到OX轴的距离aaX,将此距离在W面上由aZ向右截取,即得a″。如图1-13c所示。
截取aaX=a″aZ时,除了上述用圆规量取距离或做1/4圆弧的方法外,还可以做45°辅助线截取,如图1-14所示。
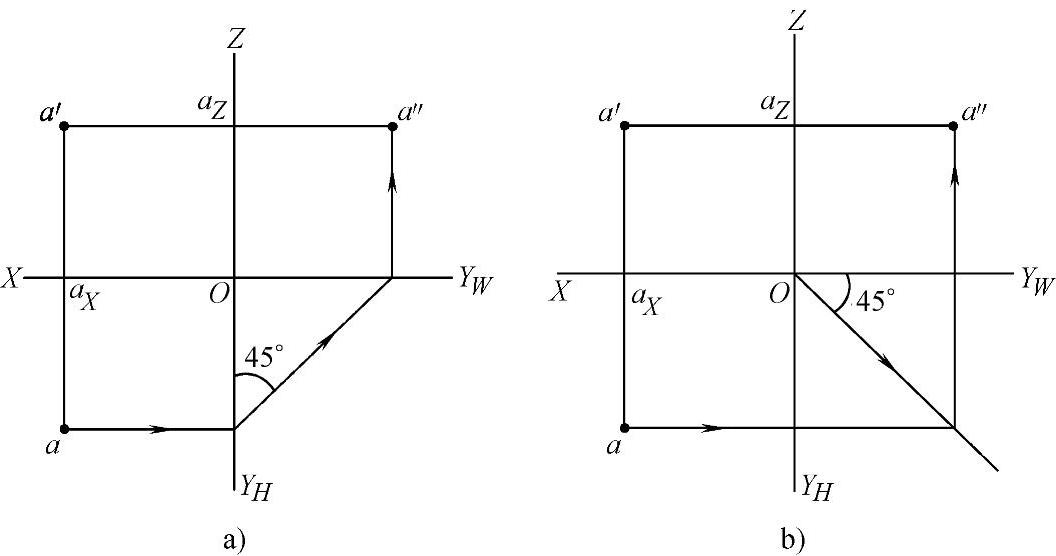
图1-14 截取aaX=a″aZ的方法
如果已知点的水平投影和侧面投影,求其正面投影,作图方法见图1-15a;如果已知点的正面投影和侧面投影,求其水平投影,作图方法见图1-15b。
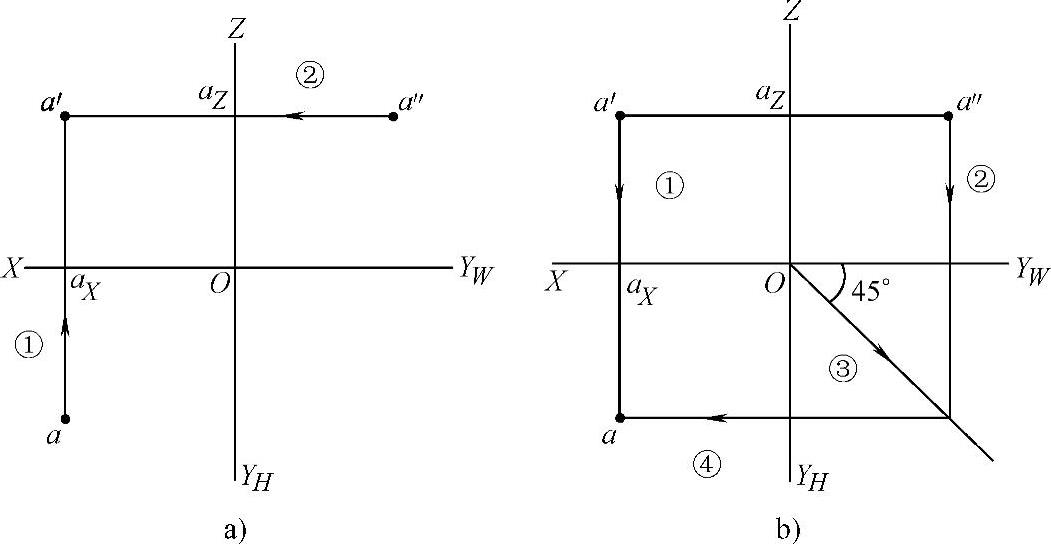
图1-15 根据点的两面投影求第三面投影
a)已知水平投影和侧面投影,求正面投影 b)已知正面投影和侧面投影,求水平投影
2.点的投影与坐标(www.daowen.com)
若将三个投影面看成三个坐标面,三个投影轴看成三个坐标轴,三个投影面的交点看成坐标原点O,则点到H面的距离可以看成点的z坐标,点到V面的距离就是点的y坐标,点到W面的距离就是点的x坐标。点的x坐标反映了点左右方向离开坐标原点O的距离,也是离开W面的距离;该距离能在V面和H面的投影上反映出来,但不能在W面的投影上反映出来。但W面上的投影却能反映出该点的y坐标和z坐标。同理,点的y坐标反映了点前后方向离开坐标原点O和V面的距离,z坐标反映了点上下方向离开坐标原点O和H面的距离。点的投影、坐标、到投影面的距离三者之间的关系见表1-1。
表1-1 点的投影、坐标、到投影面的距离三者之间的关系

例1-2 已知P点的坐标为(10,15,20),求作点的三面投影。
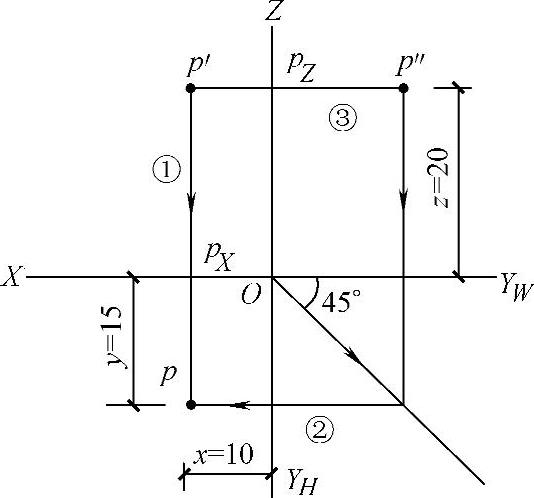
图1-16 根据坐标求点的三面投影
解:1)作一条水平线,再作一条垂直线,交于O点,标注X、YH、YW、Z轴;
2)根据x=10,y=15,作水平投影p;
3)根据x=10,z=20,作正面投影p′;
4)根据y=15,z=20,作侧面投影p″。如图1-16所示。根据坐标求出两面投影后,也可仿照例1-1的方法求解第三面投影。
3.特殊位置点的投影
第一投影区的点应当包含位于三个投影面和三个投影轴上的点,这些点称为特殊位置的点,它们的投影中有一部分落在投影轴上,甚至落在坐标原点。
1)投影面上的点,离开该投影面的距离为0,其投影落在该投影面和该投影面边界的两条轴线上。
如图1-17所示,H面上的点A,水平投影落在H面上,正面投影落在X轴上,侧面投影落在Y轴上;V面上的点B,水平投影落在X轴上,正面投影落在V面上,侧面投影落在Z轴上;W面上的点C,水平投影落在Y轴上,正面投影落在Z轴上,侧面投影落在W面上。
2)投影轴上的点,其投影落在该投影轴上和坐标原点处。
如图1-18所示,X轴上的点E,正面投影和水平投影落在X轴上,侧面投影落在坐标原点处;Y轴上的点F,侧面投影和水平投影落在Y轴上,正面投影落在坐标原点处;Z轴上的点G,正面投影和侧面投影落在Z轴上,水平投影落在坐标原点处。
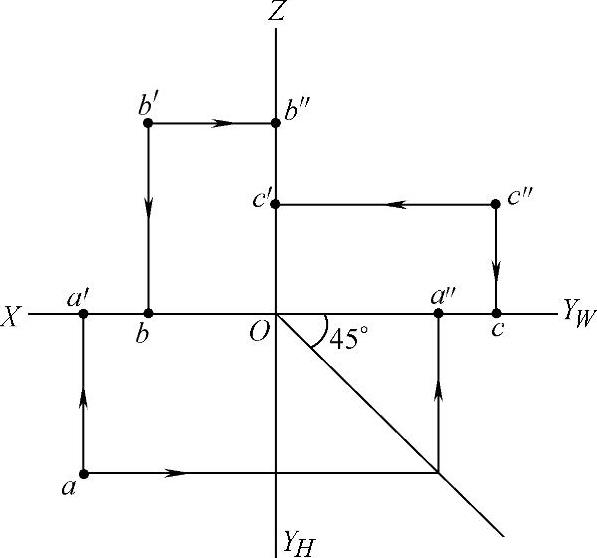
图1-17 投影面上点的投影
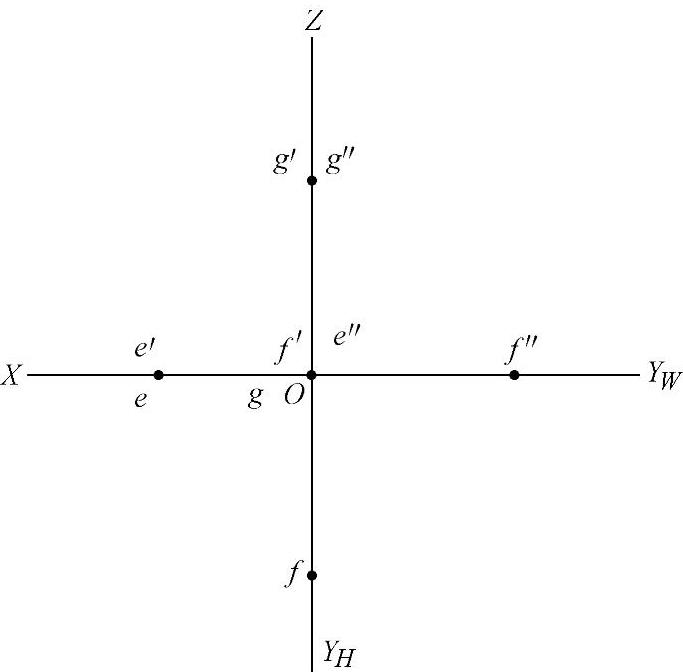
图1-18 投影轴上点的投影
4.两点的相对位置
现有两点A(10,12,8)、B(8,15,13),试比较A、B两点的相对位置。
从两点的x坐标可以看出,A点离开原点10mm,B点离开原点8mm,所以A点在B点左边2mm处,同理,A点在B点后面3mm处,A点在B点下面5mm处。因此,A点在B点的左后下方。
根据两点的三面投影,也可以很方便地判断出两点的相对位置。如图1-19所示,沿着X轴的正方向,远的为左,近的为右;沿着Y轴的正方向,远的为前,近的为后;沿着Z轴的正方向,远的为上,近的为下。
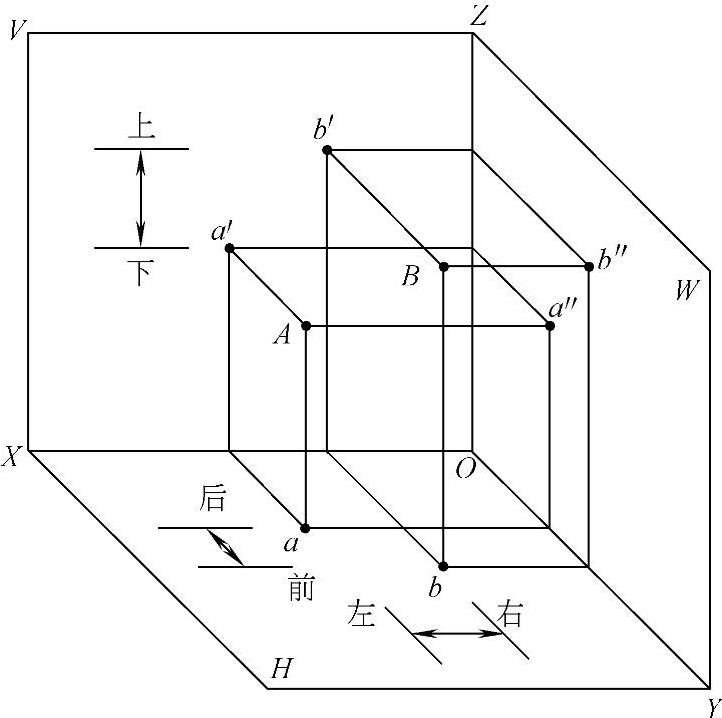
图1-19 两点的相对位置
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







