以上几种调平方法在目前支撑式作业平台的调平中应用相对普遍，调平方法有其各自的优缺点，可以从如下方面进行综合考虑：

1.水平调节量和调整效率

表6-1给出了不同调节方法各自调节量和调平效率的对比数据，其中“聚焦式”中心不动调平方法的调节量最小、调节效率最高，但这种调节方法会导致调节中平台出现巨大的抖动，所以在具体的调节环境中要根据实际情况进行优化选择。

表6-1 调节量和调平效率的比较

根据条件为α＞0，β＞0的分析得到，无论α、β参数是在第几象限取值，前两种控制方法的调节量和调平效率都具有相同的结果，仅仅在实际使用中适用不同的平台运行方向。而对于第三种调节方式，虽然调节量小、调节效率最高，但由于调节中可能产生较大的振动，所以在实际选择中需要优先选择。

2.控制系统的逻辑

对比位置误差控制方法和角度误差控制方法，可知角度误差控制可直接采用角度传感器采集的数据进行逻辑分析，通过继电器或逻辑电路实现待调点的实际调节。而位置误差控制则需要根据采集的数据进行相应的计算，获得可用来分析的位置量，所获得的控制量还需要换算为位置调节量和反馈对比数据，相对于角度误差控制方法，位置误差控制的实现过程更为复杂、控制效率低、控制成本较高。(www.daowen.com)

3.调整精度对比

采用成本较高的智能模糊控制系统来对位置误差进行控制具有较高的调节精度，调节效率同样优于角度调节。而角度误差控制方法最大的优点是其实现简单，制造成本低，但调整精度降低。

根据系统设计的要求，悬吊作业装备中平台上升运行时调平过程不宜有吊点下降的动作，悬吊作业平台下降运行时调平过程不宜有吊点上升的动作，因此调平方案Ⅲ不适合用在本系统中。高处作业悬吊式作业装备的调平在精度上要求不是很高，对于调平距离及调节时间也没有特殊要求，为了减少调平系统的设计难度，降低设计成本，因此，调平方案Ⅰ、Ⅱ也不适用。悬吊作业平台的调平必须满足检测角度超过设定值才发生，而不像方案Ⅳ中描述的，只要平台横纵向角度绝对值大于0即可进行调平；对于平台横纵向角度中某一角度超过设定值，而另一角度在设定值范围内的情况，如果控制器采用方案Ⅳ作为调平方法，则会将此情况判断为平台水平，而不采取调平动作，这样倾斜的角度会越来越大，最终导致出现安全事故。

如图6-6所示为三吊点U型平台简化模型，提升机所在的吊点分别为点A、点B、点C。根据上述分析，用于悬吊作业装备中平台系统的调平方法有别于文中用支撑式平台进行论述的方法，系统采用改进后的角度误差控制方法完成平台的调平，实现起来简单，调平效果较好。以悬吊式作业装备上升运行为例，调平过程如下。

根据平台吊点的分布特点，在调平过程中，设计成先调平X轴方向角度，再调平Y轴方向角度，这种控制逻辑实现起来简单，调平时间相对较短。在对Y轴方向进行调平时，点A、点B设置成一组，点C单独为一组。首先检测平台X轴方向角度α的绝对值是否超过设定值1.5°，若超过设定值，则执行调平程序，若没有超过设定值，则继续检测Y轴方向角度β。当α＞1.5°时，保持B点不动，A吊点上升使α值减小，当α≤ε（ε为调平误差）时，停止上升；当α＜-1.5°时，保持A点不动，B吊点上升使α值减小，当α≤ε时，停止上升，完成平台X轴方向调平。接着检测平台Y轴方向角度β的绝对值是否超过设定值1.5°，如果超过设定值，则执行调平程序，如果没有超过设定值，则继续检测X轴方向角度α。当β＞1.5°时，C吊点保持不动，A、B吊点上升使β值减小，当β≤ε时，停止上升，平台达到水平状态，调平结束；当β＜-1.5°时，A、B吊点保持不动，C吊点上升使β值减小，当β=0时，停止上升，平台达到水平状态，调平结束。

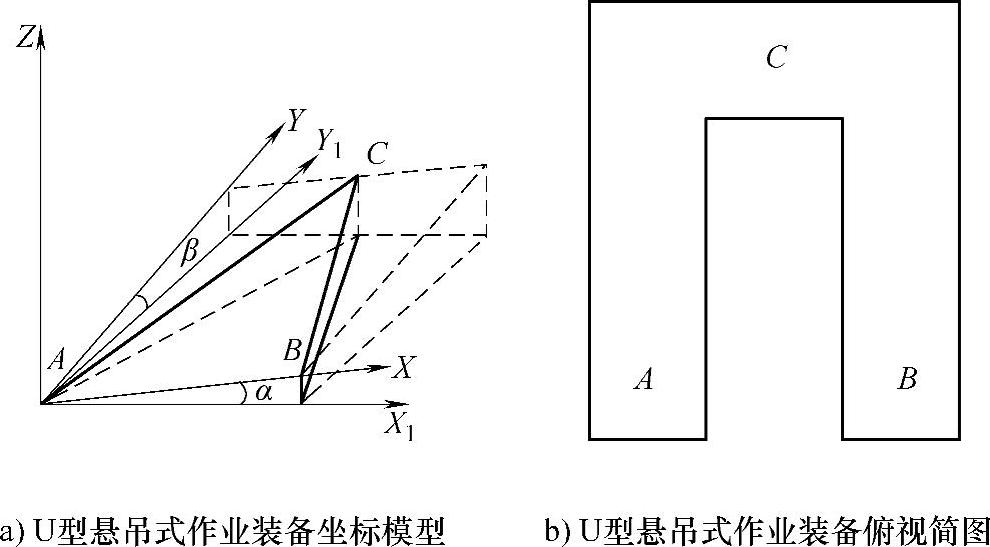
图6-6 三吊点U型平台简化模型