从控制系统的误差量方面来研究悬吊式作业装备中平台的调平问题,主要有位置误差控制调平和角度误差控制调平两个方面[24] 。
1.位置误差控制
(1)采用“赶超式”控制理论 其控制过程如图6-2所示,图中箭头高度表示平台提升点相互间高度关系。图6-2a所示为发生倾斜后各个提升点所处的状态,选择提升点中最高提升机构保持其高度不变。定位为高点位,通过控制调节其他提升点的高点使其与高点位相平,从而实现平台的水平调整,将该调整方法定义为“赶超式”最高点不动调平方法。
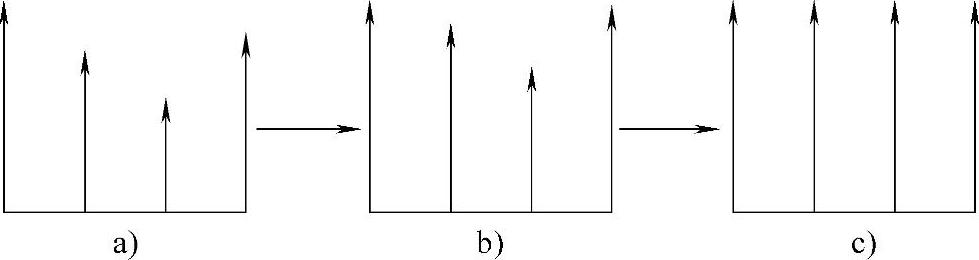
图6-2 “赶超式”最高点不动调平方法
这种调平方法中最高点的确定是其程序处理的关键点之一。如图6-1所示,当α>0,β>0时,C点为最高点;当α<0,β>0时,D点为最高点;当α<0,β<0时,A点为最高点;当α>0,β<0时,B点为最高点。
图6-1给出了平台各个悬吊点间坐标的相互关系,从中定义垂直方向的Z坐标轴原点为零,从而得到平台悬吊初始点的坐标为(x1i,y1i,0)(i=A,B,C,D),则通过变换之后,各支点的水平坐标(xi,yi,zi)(i=A,B,C,D)为
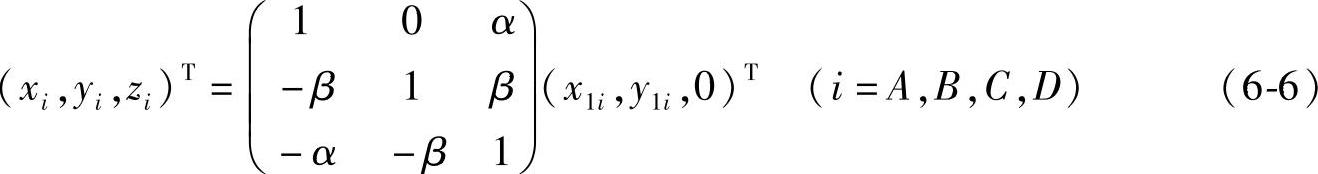
通过式(6-6)从而计算出变换后各支点在Z轴的高度误差为
zi=-αx1i-βy1i (i=A,B,C,D)(6-7)
式(6-7)给出了确定平台高点位的方法,当i=h时,确定为高点位,zi≤zh,从而可以计算获得其他提升位置与此点间的空间坐标偏移量
ei=zh-zi=-α(xh-xi)-β(yh-yi)(6-8)
不妨假设α>0,β>0,则C点为最高点,A点为最低点,可得
eC=0,eB=αLa,eD=βLb,eA=αLa+βLb,进而得到系统执行的调节距离D为
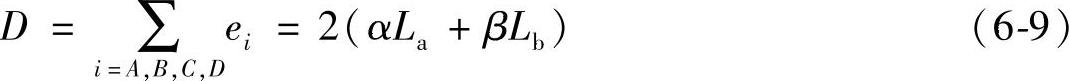
“赶超式”最高点不动调平方法的时间效率取决于各点间最大的高度差及调节中提升的平均速度
T=eA/v=(αLa+βLb)/v (6-10)
式中 T——调节效率;
v——悬吊式作业装备中平台的调整速率。
(2)“等待式”固定最低点控制理论 “等待式”控制理论与“赶超式”控制理论相比正好相反,“等待式”则强调固定各个提升点中运行最低点,称其为“低点位”。将超过低点位的提升点向低点位移动实现平台水平,其过程如图6-3所示。α,β为其调节的误差距离和调平效率的时间参数,其计算过程与“赶超式”基本相同,计算过程如下
 (https://www.daowen.com)
(https://www.daowen.com)
T=eA/v=(αLa+βLb)/v (6-12)
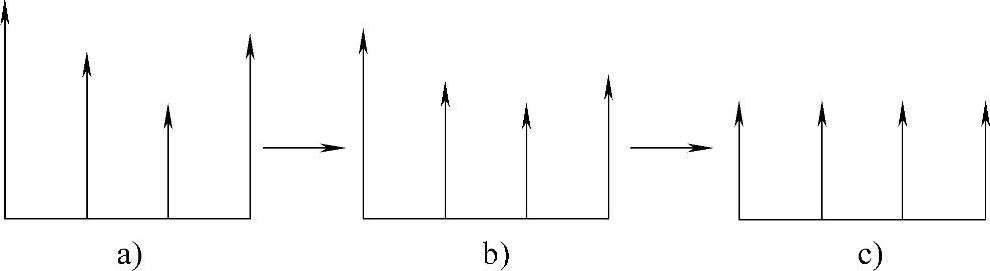
图6-3 “等待式”固定最低点调平方法
(3)“聚焦式”中心不动控制理论 “聚焦式”中心不动控制理论的调整过程如图6-4所示,调整时选定的焦点保持不动,高于焦点的提升点降低其高度,低于焦点的提升点升高其位置,最终实现平台的各点水平。
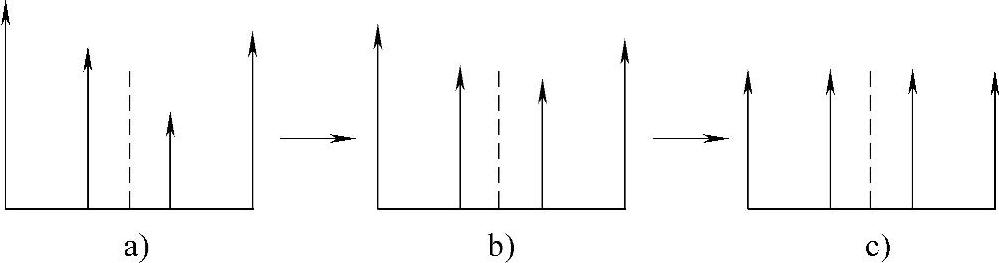
图6-4 “聚焦式”中心不动调平方法
悬吊作业装备中平台调节坐标系下的实际坐标表示为(x1i,y1i,0)(i=A,B,C,D)。认定的调节焦点坐标在水平坐标系中表示为(La/2,Lb/2,0),将其变换后,得到坐标为
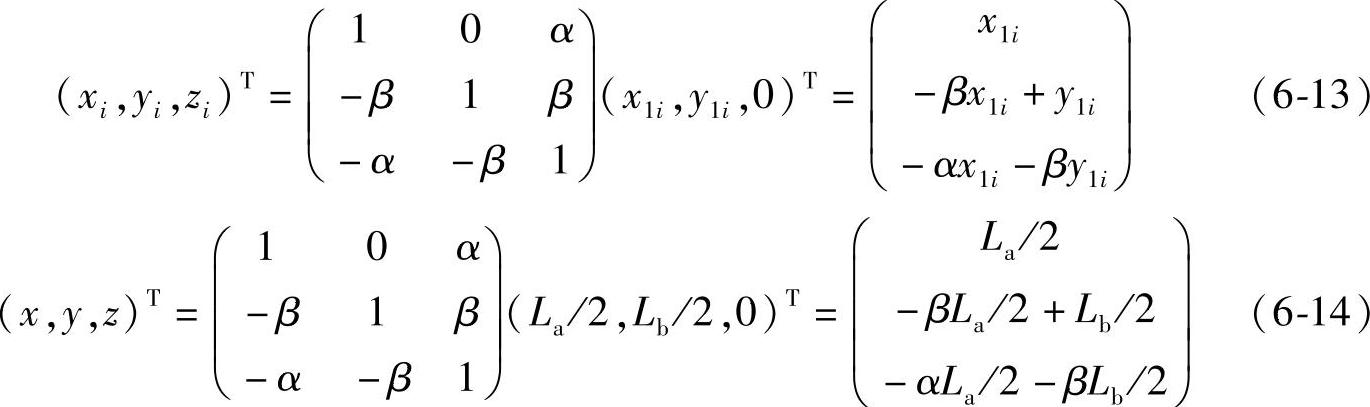
通过上面公式可以得到,在垂直方向即Z轴方向上焦点与其他提升悬吊点间的误差值为
ei=zi-z=-α(x1i-La/2)-β(y1i-Lb/2)(i=A,B,C,D) (6-15)
按α>0,β>0,可以认定提升点C高于焦点,而提升点A则低于焦点。控制的效率时间则取决于距离焦点最远点调整到焦点的调节时间,其调整距离可用最高点到焦点距离与最低点到焦点距离相叠加得到
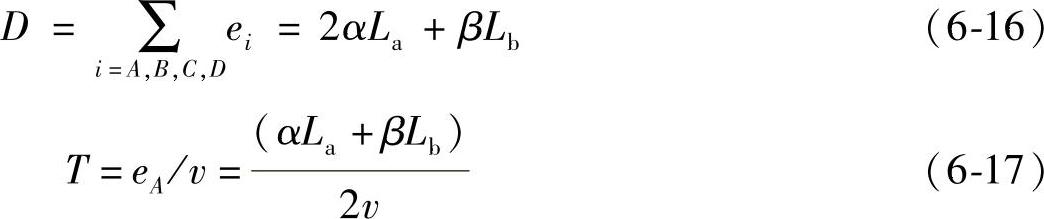
2.角度误差控制
角度误差控制是调平问题中控制系统误差量的另一方面,角度误差控制与位置误差控制可通过采集变量的换算进行相互转化。采用角度传感器测量形成控制回路的控制过程,其角度控制更为直观,即调节变量为平台垂直变化范围内的角度不平量α、β。同样采用调节提升点所处的高度位置,逐渐使平台角度趋近于零的调平控制过程,具体调平过程如下:
当平台变量α>0,β>0(α、β正方向的设定同上)时,保持C(A)点不动,A、D(B、C)吊点同时上升(下降)使变量α值减小,当α=0时,停止上升(下降);然后A、B(D、C)吊点提升(降落),则变量β会逐渐缩小,满足β=0,完成调节。实现变量α、β趋近于零,使被调系统满足控制要求。
另一种情况,当α>0,β<0时,控制B(D)提升端位置固定,A、D(B、C)吊点同时上升(下降)使α值减小,当α=0时,停止上升(下降);然后C、D(A、B)支点提升(降落),则变量β会逐渐缩小,满足β=0,完成调节。实现变量α、β趋近于零,使被调平系统满足控制要求;在完成其他状态的调整中,同样可以采用这样的处理方法实现控制平台的水平调整。
针对平台出现的不平度α、β,在调整过程中需要选择适当的调整参数优先进行调整,调整时需要其他提升点维持相对基点位置距离不变。倾斜角度调平控制流程如图6-5所示。
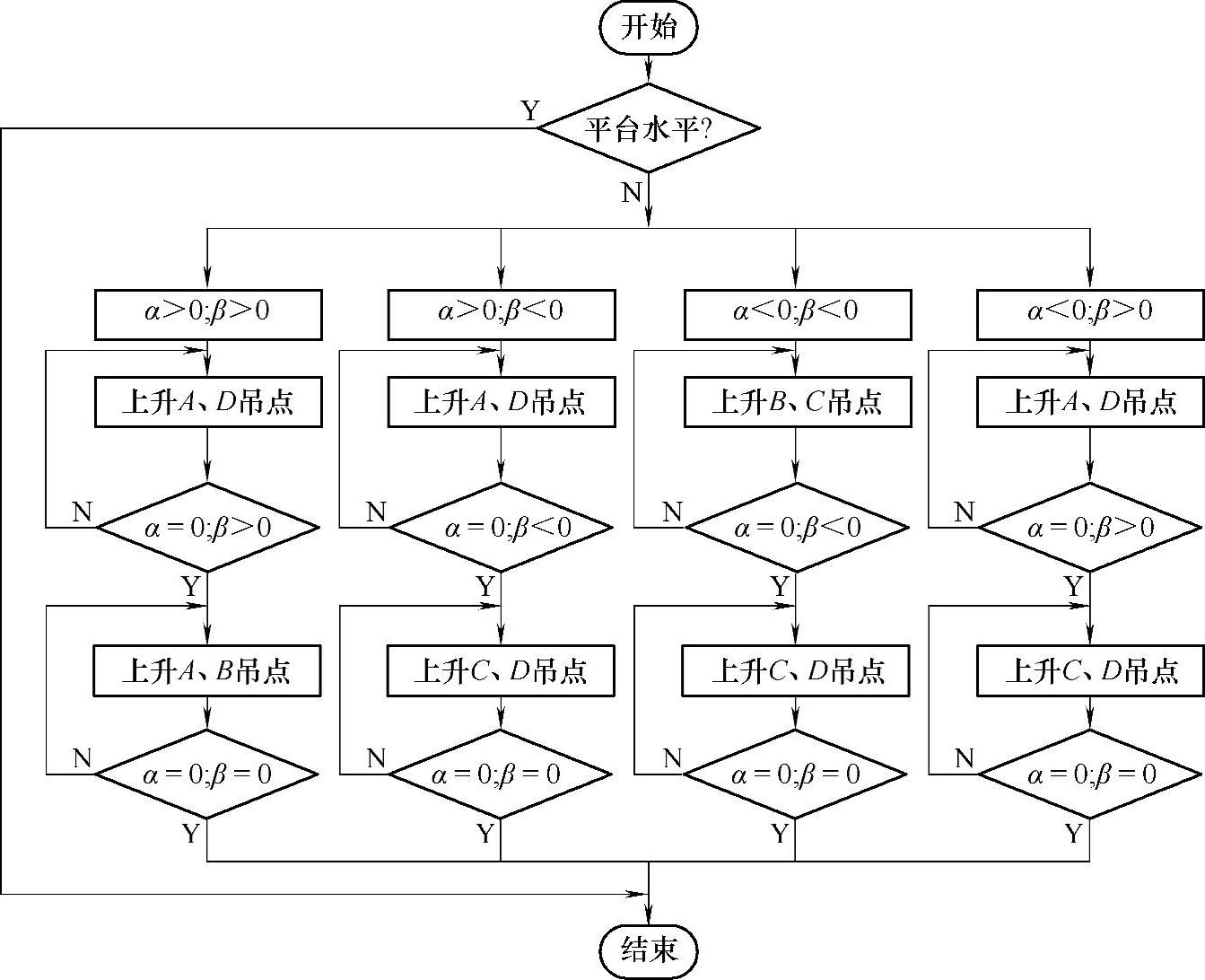
图6-5 倾斜角度调平控制流程
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







