目前,对悬吊作业中普通平台的单边倾斜现象,常规的解决方法是通过手动方式控制提升机构单边升降来进行平台的调平。这种处理方式不仅操作步骤繁琐,而且调整精度无法得到保证,整个调整过程在高空完成,其操作存在一定的危险性。同时,在悬吊作业装备使用过程中,若装备的提升机构出现超载运行或出现堵转现象,而操作人员没有及时处理,也容易导致坠落安全事故的发生。
根据“三点或两条相交直线确定一个平面”的数学理论,悬吊作业平台的调平实质是将平台上两条相交直线调成水平。基于这样的理论推导,当作业平台上的两条直线相互垂直时,它们在各自的调平中才不会发生耦合现象。实际工程中具体的调平方法可以叙述为:在平台中心点处安装用来测量悬吊作业装备中平台垂直轴倾斜度的角度传感器,通过数字化电路处理采集得到的倾斜角度,传递给中央运算器,通过运算得到调整控制量,再通过执行模块来驱动平台向倾斜角度相反方向调平[49] 。
假设平台有四个吊点,分别为A、B、C、D(图6-1),记平台长度AB=La,记平台宽度BC=Lb。
当获得不同坐标系间相互转换的转换矩阵,可以很容易地将其中一个坐标系下的坐标点转换到另一个坐标系下,假设控制任一坐标点坐标为(i1,j1,k1):
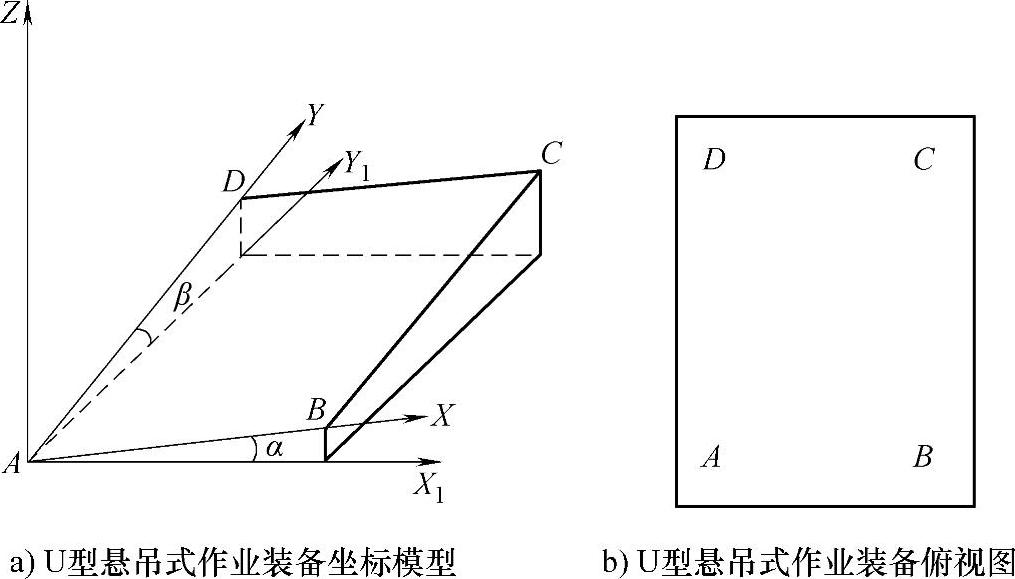
图6-1 四吊点U型平台简化模型
当α≠0,β=0时,坐标变换为(i2,j2,k2),则根据坐标变换,可以得到
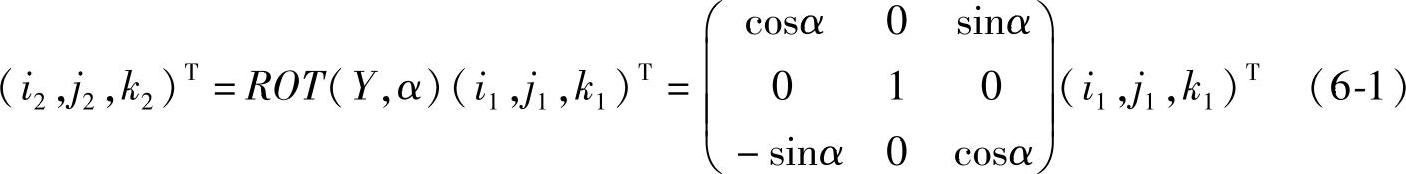
当α恒定,而β≠0时,可以通过坐标变化将其变化为(i,j,k),进而得到(https://www.daowen.com)
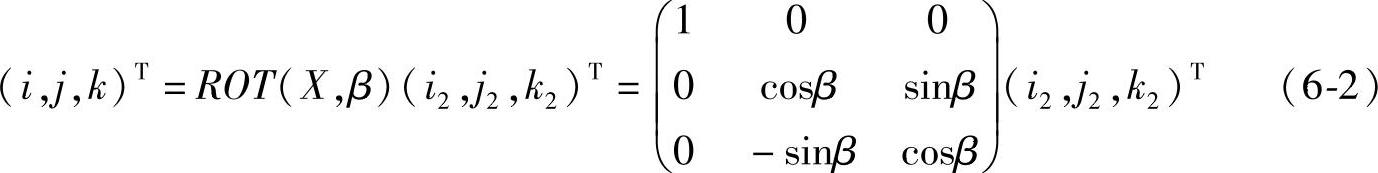
经过α,β变换后,初始化的平台坐标(i1,j1,k1)变为(i,j,k)T
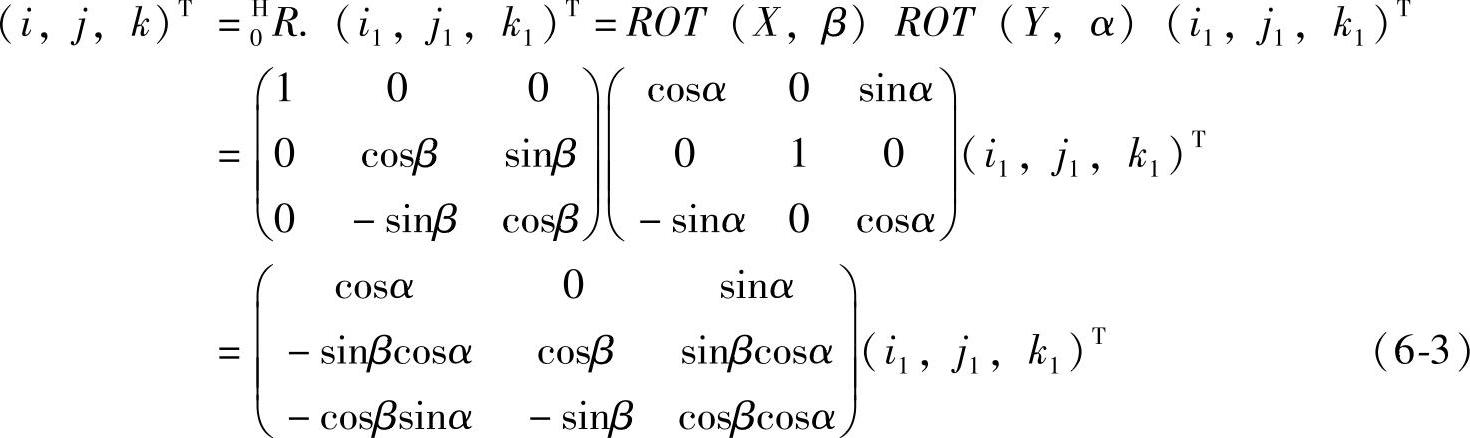
假设平台调平时,水平基准面上的纵横向倾角很小。因此,可以忽略高阶,近似得到cosα=cosβ=1,sinα=α,sinβ=β。则0HR可以化简为
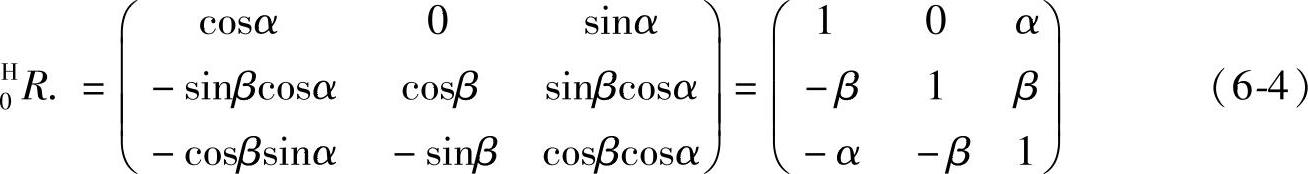
从而,初始化的平台坐标(i1,j1,k1)变为(i,j,k)T
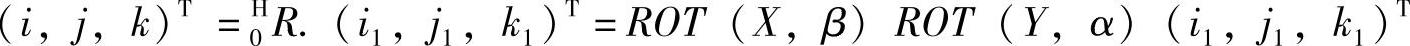
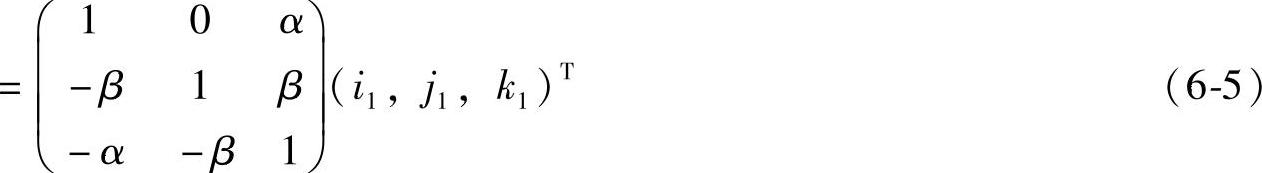
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





