提升机构的传动性能作为研究对象常具有强耦合、非线性特征，因此采用常规方法几乎无法给出其准确的数学模型。柔性摩擦传动系统数学模型主要考虑钢丝绳的缠绕角度、绳轮对钢丝绳的包围弧度、钢丝绳的纯拉力及在拉力作用下的变形比等参数，对这些参数中产生控制性矛盾的量进行控制，通常需要解耦处理十分复杂。而采用假设模态法和奇异摄动理论将数学系统转变为快变和慢变子控单元是解决此类问题的有效方法。

在对传动性能的控制中，结合奇异摄动理论处理系统中多参数耦合问题，以数学中的拉格朗日方程为基础建立快慢子控单元，采用最优控制方法解决问题形成两个单变量参数方程，最终给出了设计的控制器，并通过仿真验证其有效性。

在悬吊作业平台的摩擦传动过程数学模型的控制中，采用双时标模型方法，将系统中主要参变量进行划分，对钢丝绳的缠绕角度，绳轮对钢丝绳的包围弧度，钢丝绳的纯拉力及在拉力、滑移速度等参数以慢变量进行处理，将传动角速度、摩擦力处理为快变量，进而建立最优控制的控制策略，给出合理的控制参数调整和选择。

根据所提出的控制方案，结合系统动力学方程，采用Matlab软件建立悬吊平台多点控制系统仿真模型，如图5-53所示。从提升机构运动分析宏观系统上考虑，提升机构的运动是由速度给定、速度检测、速度控制组成的速度闭环，从而实现按照给定的速度曲线自动运动。提升机运行速度v=f（t），根据动力学方程，可以得到运动所需要的转矩T_e=f（t），从而得到传动系统所需作用力F=f（t）。

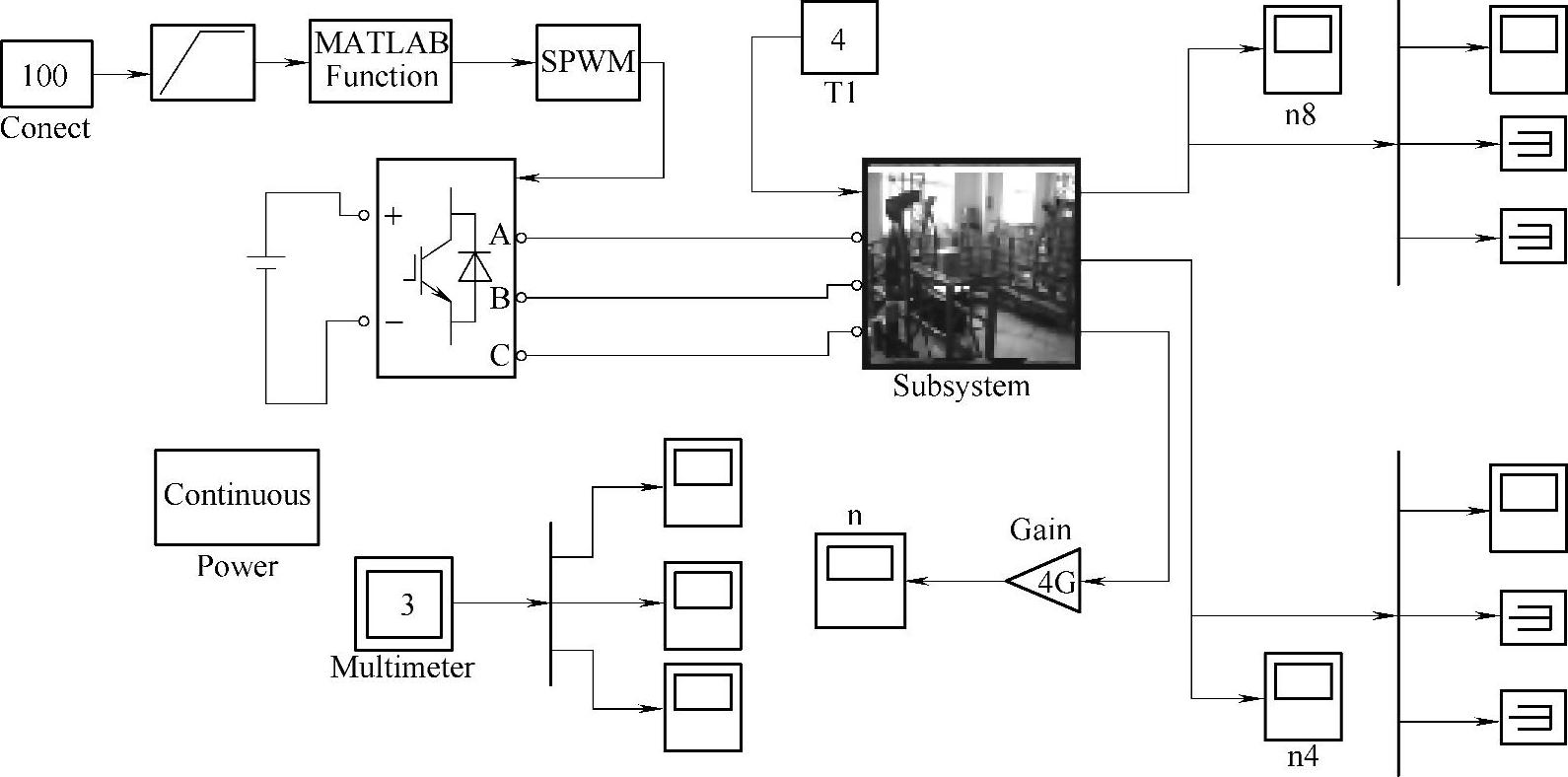
图5-33 悬吊作业平台系统模型

提升机的负载静力F_l由提升机承受的静张力差决定，在特定的平衡提升机构中，静力也就是提升物的载重F_l=mg。由于提升机构的负载为位能负载，所以静力F_l的作用方向始终是提升重物的重力方向，而与系统的运动状态和方向无关。基于奇异摄动理论，设计降阶的滑膜控制器建立仿真模型，设计中考虑了滑动模态参数及有限时间收敛问题。

1.双时标控制方法研究

由于柔性提升机构不仅是一个刚柔耦合的非线性系统，还是系统动力学与控制理论相互耦合的非线性系统，所以针对所提出的动力学模型选取准确有效的控制策略及控制方法，是实现系统稳定性的前提。

通常情况下，复杂的机械系统中存在宏观运动和微观运动共存的情况，是否放大微观运动需要根据实际情况进行确定。在柔性动力学系统的处理过程中，通常需要考虑微观运动在一个宏观机械内附有一个局部力学系统构成的宏-微机构系统。在系统中，局部力学的物理参数如钢丝绳的接触形式和接触力等比宏观机构变形要小许多，因此在研究中可以采用奇异摄动理论将系统中微量变化处理为正向的摄动。采用奇异摄动理论建立系统中快慢子单元是处理宏观和微观共存模型的有效方法。在处理微变动过程中，采用比例缩放方法将微量变换系数放大，进而建立鲁棒控制器解决系统中控制参数弱化问题，即为双时标控制方法。

采用变量分离方法设计慢变和快变子单元，将系统中微动量用奇异摄动量处理，形成控制器并分析其控制效果。在柔性摩擦传动过程中，采用假设模态法和奇异摄动理论，将原整体模型转化为宏观变化量和微观变化量的叠加是常用的处理方法。

在实际控制问题中，由于悬吊平台在空中执行平动及微量振动过程中所形成的数学模型是一个多变量的隐函数方程，具体的求解过程需要考虑模型的耦合问题，采用最优控制理论进行求解可能会导致较大的计算误差出现，因此需要将模型系统分解处理。

通过对先进的控制方法进行分析，得出现有的很多控制策略及控制方法都具有较强的针对性，或是建立在精确模型基础上。而柔性钢丝绳提升机构由于摩擦力、结构阻尼、负载变化和外部的干扰等难以进行准确建模，针对系统的强耦合性、高度非线性及不确定性的存在可能会导致控制性能的降低。将针对调整系统的动力学方程，基于奇异摄动理论将柔性动力学模型分解为快变、慢变两个子系统，并设计对快变、慢变两个子系统降阶处理的双时标滑膜控制器。设计中充分考虑系统参数的不确定性，通过滑动模态控制器使系统工作状态向滑膜面收敛。控制作用将使系统沿该平面回归系统设定位置。使系统控制特性和参数仅与模型本身参数有关，从而使控制获得较强的鲁棒性。

研究奇异摄动控制理论常有两种处理方法：一种方法是采用幂级数处理，将控制参数中积分项用幂级数的奇异摄动参数表示，并略去其中的高次幂项，获取控制参数中挠度等的近似逼近；另一种方法采用控制量变化范围不同将控制模型分解成两个或多个子单元实施单元控制叠加方法。对于有弹性材料参与的控制系统，多选用方法二来实现对系统的控制，这种方法可以将系统中的柔性伸缩变化处理为快变单元，采用纯弹性处理方法解决，而对于刚性部分则等效为慢变控制单元进行控制，最后将常规方法可以解决的慢变单元与弹性控制的快变单元进行复合控制。研究中将弹性控制模型划分为快慢两个不同的单元，划分过程中采用了经典的奇异摄动理论，成功地规避了弹性伸缩量的测量，整个控制系统由控制和观测两个子系统组成，系统在控制力跟踪上满足设定精度要求。但为减少系统的控制时间，通常需要相应降低假设的摄动参数，以适应模型精确计算，这样一对矛盾体是奇异摄动理论应用在双模式控制系统下的重要控制点，决定了控制系统的控制效果。

Sun等人的研究工作得到了较大的推广应用，形成了一整套用于解决运动源轨迹跟踪问题的处理方法，降低了对参数的精度要求，使弹性变形控制在特定条件和作用力下满足设计要求，研究了两个摩擦部件操作柔性振动负载问题，利用数学降阶方法建立了理论描述模型，并在模型的基础上设计了控制器。

2.双时标控制器设计

柔性提升机构的控制方程，当参数ε∈（0，1），采用奇异摄动理论可给出动力学方程

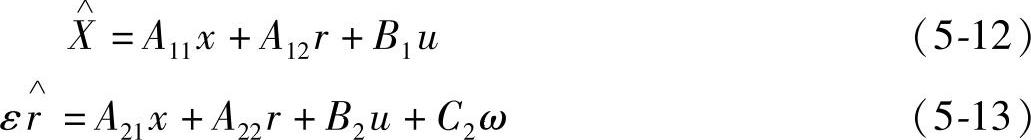
式中 ，，，，，，。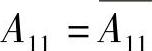

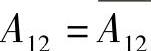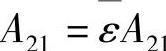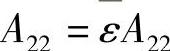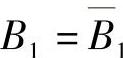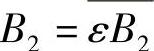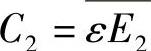当参数ε∈（0，1）趋近于零时，根据阶段参数变化的快慢，可以将上述控制系统方程分解为快变子系统和慢变子系统。分解后，控制方程对系统中变量的描述更具针对性，子系统分别对应着快变子模型和慢变子模型。

为了便于设计快变子系统控制部分，将系统方程改写为如下形式

式中 u_k、ω_k、r_k——快变子模型中与u、ω、r相对应变量，这些变量与慢变子模型对应变量之和等于对应总变量数值，即u=u_k+u_m，ω=

ω_k+ω_m，r=r_k+r_m。

如果选取ε为钢丝绳在垂直段和弯曲段的伸缩变形率，即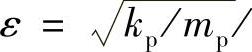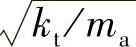。将系统中的x₁、x₂定义为慢系统的参数变量，r₁、r₂定义为快系统的参数变量，两个变量为智能调整控制扩展提供了接口数据。由于A₂₂为赫尔维茨矩阵，调整系统的快速模型是一个常规的稳定模型。其中，u为不确定的系统参数。

当不确定参数存在最大值时，可以根据通用逼近性定理，对系统中的参数进行逼近。定义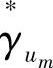的最优参数估计为

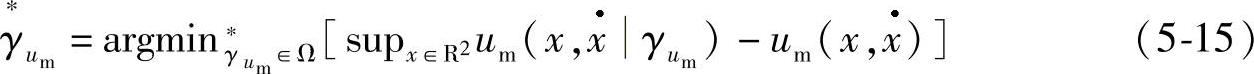
可定义最小逼近误差项 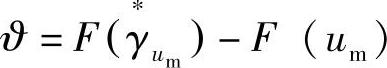，进而假设最小逼近误差ϑ有界。通过对应期望值与实际值的差值，获得系统的误差来定义滑膜界面，具体公式如下

式中 e=[e₁，e₂，e₃]^T；

s=[s₁，s₂，s₃]^T；

τ=diag（τ_i），τ_i＞0，i=1，2，3。

根据实际系统参数的变化范围，通过数值计算发现，选择合适的系数矩阵可以有效地提高滑膜系统跟踪性能及系统稳定性。

为了便于推导慢变子模型结构，将系统模型进一步简化为：A₀=A₁₁-A₁₂A₂^-₂¹A₂₁，B₀=B₁-A₁₂A₂^-₂¹B₂，C0=-A₁₂A₂^-₂¹C₂。考虑慢变子模型系统中存在的不确定性因素，慢变子模型系统方程整理后得

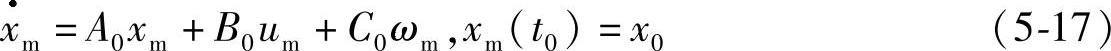
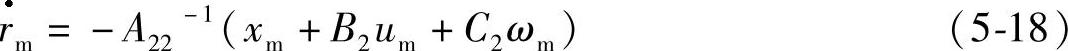
式中 x_m、u_m、ω_m、rm——慢变子模型中与x、u、ω、r相对应变量的分量。

控制器设计主要集中在动力系统分解后的慢变子系统中。慢变子模型的方程可以表示为

(www.daowen.com)

式中 D——未建模的高阶动态变量。

根据式（5-12）、式（5-13）对控制系统进行具体化，可以将A₀、B₀、C₀ω+D分别表示为A₁₁、B₁、C，进而式（5-19）可以简化为

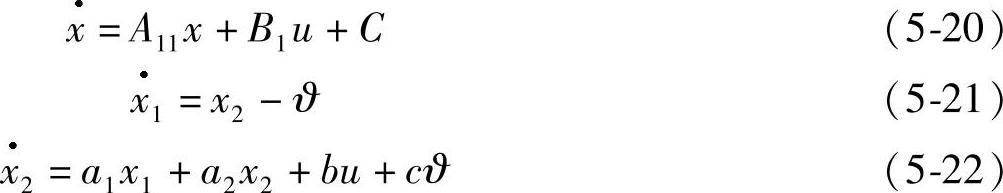
式中 ϑ——系统中不确定因素引起的系统扰动变量。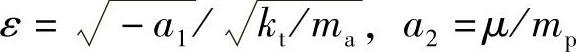，确定变量a₁和a₂，从而式（5-21）、式（5-22）构成了一个有界的不确定干扰项的二阶线性系统。根据滑膜控制原理，选择如下函数形式作为滑膜控制函数

s（t）=τx₁+x₂ （5-23）

其中，将s（t）=0定义为滑膜的超平面，根据滑膜控制条件，控制率u应该设计满足下述不等式

在没有外界干扰的条件下，处于滑膜控制下的系统等价控制量u_d可以通过设定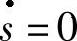来获取，其具体计算公式如下

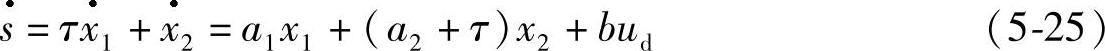
u_d=-b^-1（a₁x₁+（a₂+τ）x₂） （5-26）

因此，系统的控制率u由滑膜系统选择控制率u_x与等效控制率u_d组成，其中u_x用来保证控制参数在滑膜表面活动，即

u=u_d+u_x （5-27）

在调整控制系统中，平台和提升机构质量及悬空段钢丝绳质量m_p是在一定的范围之内变化的参数，受下面方程控制

0＜m_p1≤m_p≤m_p2 （5-28）

定义b_min=1/m_p2，b_max=1/m_p1，则可以得到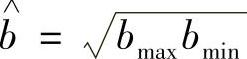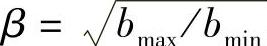，。降阶处理后的扰动和外部干扰控制率方程可以表示为

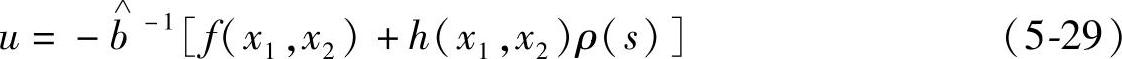
式中 ρ（s）=sgn（s），选择率的定义函数；

f（x₁，x₂），h（x₁，x₂）——f（x₁，x₂）=a₁x₁+（a₂+τ）x₂，h（x₁，x₂）=|（β-1）a₁x₁+（a₂+τ）x₂|+β（η+Θ），其中η是常

数，ΘK_p（N/m）是外界干扰引入的有界函数。

模型设计中多参数控制规则式（5-27）在系统仿真中使调整控制表现出较好的稳定性，并对模型参数中振动的不确定性具有一定的鲁棒性。

3.双时标控制器与其他控制器对比分析

为了验证系统控制策略的有效性及模型建立的准确性，对摩擦式钢丝绳提升机构调整控制模型进行了数值仿真。控制系统采用设计的快、慢分布参数的双时标尺度控制策略，对存在不确定性参数慢变子系统，可以采用观测器理论实现系统反馈控制，进而抑制钢丝绳振动^[48]。

摩擦驱动提升机调整系统相关参数见表5-16。

表5-16 摩擦驱动提升机调整系统相关参数

系统的仿真在[0，5]s时间间隔内进行。仿真过程中需要模拟提升机在柔性钢丝绳振动产生的干扰，该干扰采用典型震荡衰减方程输入，输入方程式为∂e^-φt[cos（8πt-π/2）]/2，系统干扰输入函数曲线如图5-34所示。

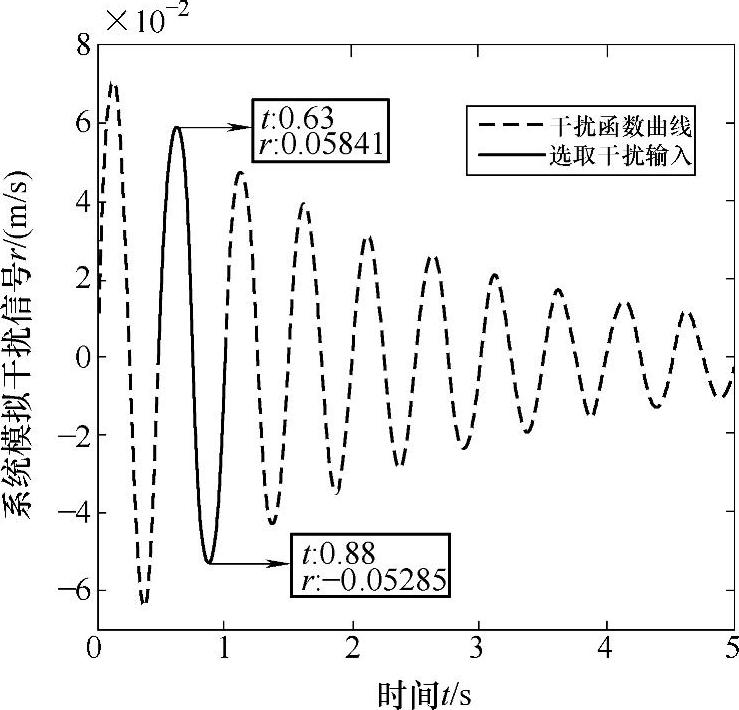
图5-34 系统干扰输入函数曲线

其中实线曲线为截取干扰输入，输入干扰时间为0.5～1s时间内，干扰波峰位于0.63s处，波谷位于0.88s处，在其他时间内无干扰，系统仿真采样率设定为0.01s，采样500次。

仿真过程由Matlab仿真软件完成，在系统稳定性和振动消除方面，通过对模型控制系统与常规的被动控制、二次型调节控制方法的对比研究，得到了三种不同的控制策略对调整系统垂直振动距离的调节曲线，如图5-35所示。仿真过程中二次型调节控制的参数选择采用比例调节，调节比例状态空间形式得到线性系统，目标函数为提升机构的状态参数及控制输入变量的二次型函数。状态反馈控制器的κ使二次型目标函数J取最小值，通过权矩阵Q与R决定参数κ值。由于研究内容属于非线性系统控制器设计问题，因此，其性能指标不能完全被状态变量和控制变量的二次型函数的积分表述。

通过仿真数据结果，可以看出，采用双时标变换阶段参数化分解模型的智能控制策略和二次型调节控制均具有较好的控制稳定性和调节速度，而常规的被动控制则表现出与干扰信号源相近的震荡衰减曲线，该控制策略在仿真过程中未使系统达到稳定状态。为了更好地对智能控制和二次型调节进行对比，图5-36将仿真曲线进行了局部放大，从放大图可以清楚地看到二次型控制产生了小幅度的过渡调节。二次型调节产生的这种过渡调节主要是由于所控制系统中的弹性振动引起，表5-17给出了详细的关键点数据。

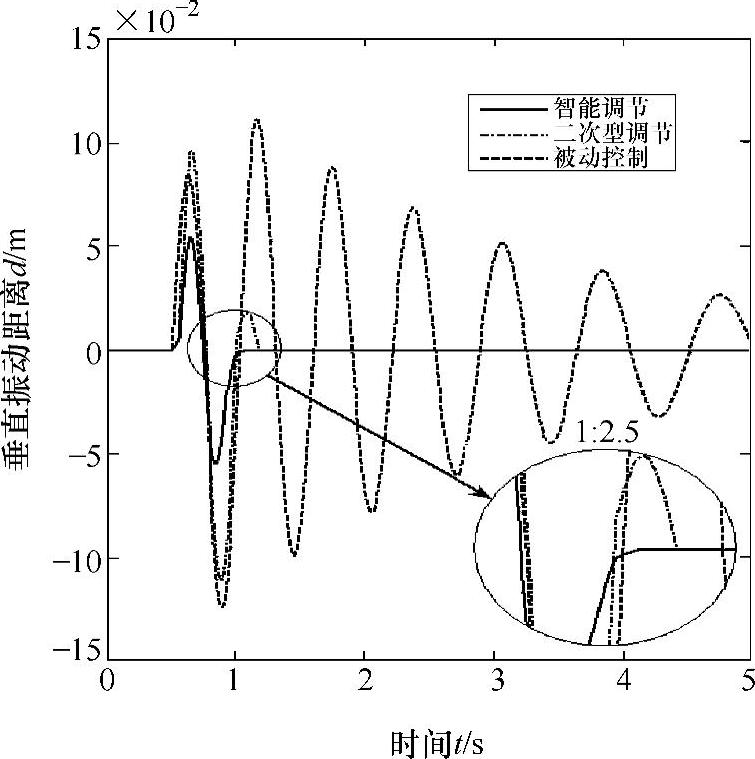
图5-35 不同控制策略仿真对比示意图

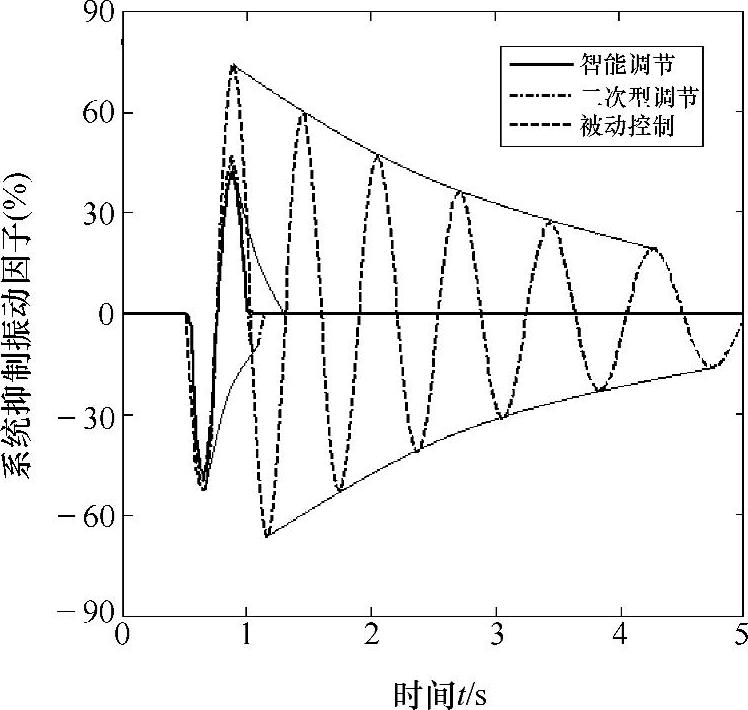
图5-36 仿真系统抑制振动因子

表5-17 仿真对比曲线关键点数据

通过图5-36可以看出，采用双时标变换阶段参数化分解模型的控制系统，控制过程有效。在控制时间和抑制震荡方面优于其他两种控制方式，这主要是由于慢变子系统和快变子系统可针对控制过程中系统存在不确定性，采用自适应模糊滑膜控制器，实现了系统的轨迹跟踪；而对系统中系统参数表现出的摄动影响，采用能够抑制系统的弹性振动的鲁棒最优控制。该控制器以控制平台振动加速度最小为优化目标，通过调整可调节压绳器的阻尼力，减少了动作过程中的振动，调整智能系统控制的进一步研究是控制器执行过程中的振动问题。