研究采用模糊PID控制理论，使整个调节过程更加平稳，缩短调整时间；同时运用仿真软件对控制算法进行仿真，定量分析控制策略的优劣，并进行修正，缩减调试时间，提高系统开发效率。

1.模糊PID控制方法研究

由于机械加工误差、载荷分布、摩擦传动参数、高空中风载因素等都可对提升机构传动性能造成影响，采用传统的单一PID控制器不能很好地满足控制需要。经过实际分析，利用模糊控制器在线整定PID控制器参数的自适应模糊PID控制可较好地满足要求。自适应模糊PID控制可根据外部情况变化，随时调整PID控制器中的K_P、K_I、KD三个参数，以使高空作业平台有最好的调整效果。

模糊控制是建立在人工经验基础上的控制方法，其控制结构如图5-11^[46] 所示。

整个模糊理论的控制过程依次分为信息的模糊化、模糊推理和模糊量的精确化构成。其中模糊化是将通过传感器等设备测量到的外界参数通过模糊集合的隶属度函数转换对应到相应论域的模糊子集中。模糊推理即根据模糊规则库中的规则对模糊化的结果进行分析推理得出结论，模糊规则库由有经验的操作者及专家根据其自身的实际经验及理论知识制定，是人类智慧的结晶。模糊量的精确化是根据模糊推理得出的模糊控制量，使用相应方法得出一个最具代表性的精确值作为控制量驱动被控对象。

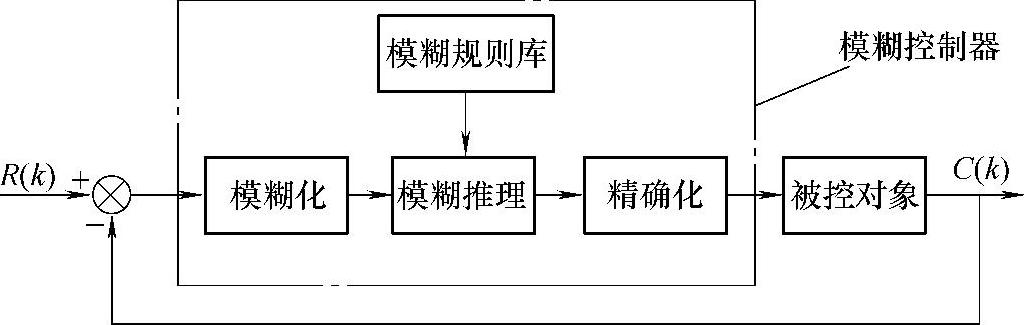
图5-11 模糊控制器结构

模糊控制是以模糊集合论为其数学基础，是建立在人工经验基础上的，适应于无数学模型的研究对象，其鲁棒性强，但是模糊控制为有差控制，无法完全消除系统残差；传统PID控制的控制参数固定，决定其无法满足复杂非线性时变系统控制的需要，故也不易采取传统的PID控制。因而可以通过模糊和PID相结合的控制方法弥补各自的缺点，即可消除单纯模糊控制方法下的残差问题，也可解决单一PID控制对复杂系统工况难以应对的问题，两者结合可明显提升控制效果。

传动性能模糊PID控制方法的研究过程：

1）控制系统的硬件设计。根据系统的实际需求，综合稳定性、实现难易度、经济性等多方面因素来选定最合适的控制器作为系统的主控单元。围绕系统所要实现的功能及选定控制器的具体要求对外围硬件电路进行优化设计。最后使用Altium Designer制图软件设计本系统的硬件电路并完成其原理图的绘制，制出PCB电路板。硬件电路搭建完毕后对系统软件进行研究设计，并对程序进行可靠性、稳定性分析，保证系统的平稳运行。

2）模糊PID调整算法研究。对模糊控制理论和PID控制理论进行深入研究。以模糊控制和PID控制基本理论为基础，研究分析模糊PID控制理论的基本原理，并根据悬吊式平台的实际情况来编写调整算法，使应用此算法的悬吊式平台调整效果更加精确、平稳、缩短调整时间，达到稳、准、快的三个控制指标要求。

3）对制定的模糊PID调整算法进行量化仿真分析。结合分段调整的控制策略，实现系统的多控制步骤，利用Matlab中的Simulink仿真模块对编写的调整算法进行建模，仿真分析。对算法中的各个参数进行量化，针对量化结果进行优化。通过对各参数的优化，提高悬吊平台的稳定性与适用性。

2.模糊PID调整控制器设计^[47]

（1）系统参数的模糊化 根据自适应模糊PID控制系统的结构图得出，此模糊控制器中有倾角偏差e（k）和倾角的偏差变化率e_c（k）两个输入量，K_P、K_I、K_D三个输出量，首先要把这五个精确量转变为模糊值，确定其基本论域和模糊子集论域。基本论域倾角偏差e（k）和倾角的偏差变化率e_c（k）等输入量和K_P、K_I、K_D三个输出量的具体实际范围值，模糊子集论域指基本论域乘以模糊因子后的论域。

1）输入量的模糊化。根据国家标准，当高空作业平台倾斜量达到8°时，其自身装配的安全锁就会发生作用锁紧安全锁钢丝绳，停止高空作业平台的任何动作。故根据此实际情况，将高空作业平台倾角偏差e（k）的基本论域X_e设为[-8，+8]，单位为（°）；倾角偏差变化率e_c（k）的基本论域X_ec设为[-3，+3]，单位为（°）/s。设其模糊子集论域均为[-6，+6]，模糊子集为{NB，NM，NS，ZO，PS，PM，PB}。故倾角偏差e（k）和倾角偏差变化率e_c（k）两变量的模糊因子为

2）输出量的模糊化。输出量为PID控制器中比例系数K_P、积分系数K_I、微分系数K_D的三个参数的调整量，其中ΔK_P的基本论域为[-0.6，+0.6]，ΔK_I的基本论域为[-0.012，+0.012]，ΔK_D的基本论域为[-1.2，+1.2]。其模糊子集论域均为[-6，+6]，模糊子集为{NB，NM，NS，ZO，PS，PM，PB}。故比例系数变化量ΔK_P、积分系数变化量ΔK_I、微分系数变化量ΔK_D的模糊因子为

3）输入输出量的隶属函数曲线。经过研究分析，考虑到高斯型隶属函数曲线运算量较大，本系统的CPU处理时有可能会出现延时状况；而三角形隶属函数曲线运算量小，且其控制效果完全可满足本系统的设计要求，故控制器选用三角形隶属函数曲线。本模糊PID调整算法全程基于Matlab中的Simulink模块构建，其各自隶属度函数曲线在Matlab整定情况如图5-12～5-16所示。

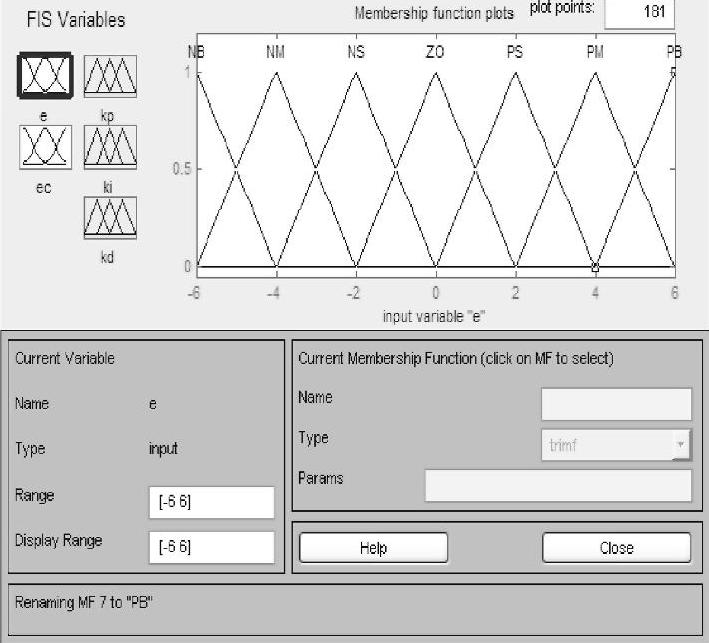
图5-12 整定e隶属函数曲线

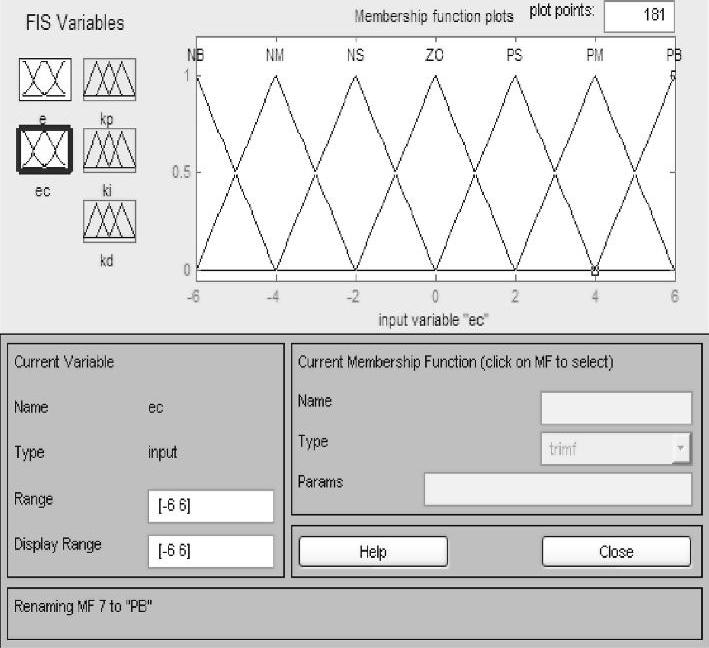
图5-13 整定e_c隶属函数曲线

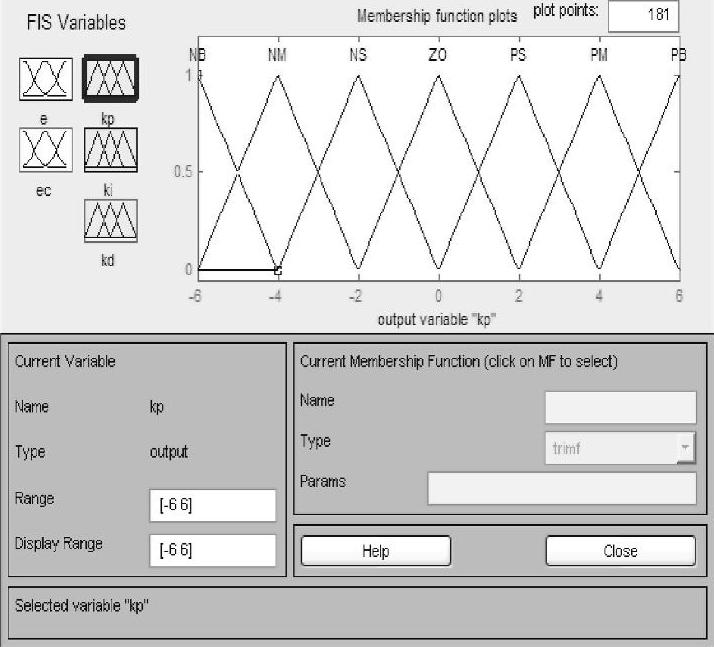
图5-14 整定K_p隶属函数曲线

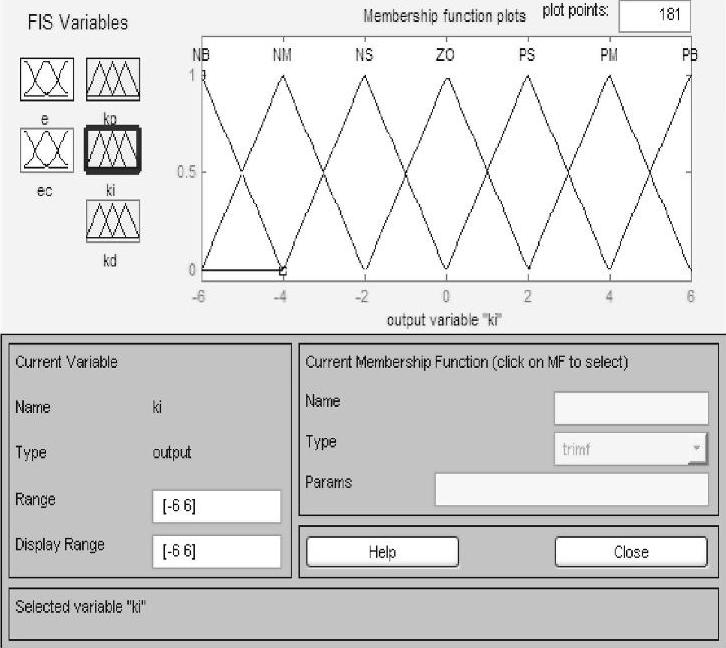
图5-15 整定K_I隶属函数曲线

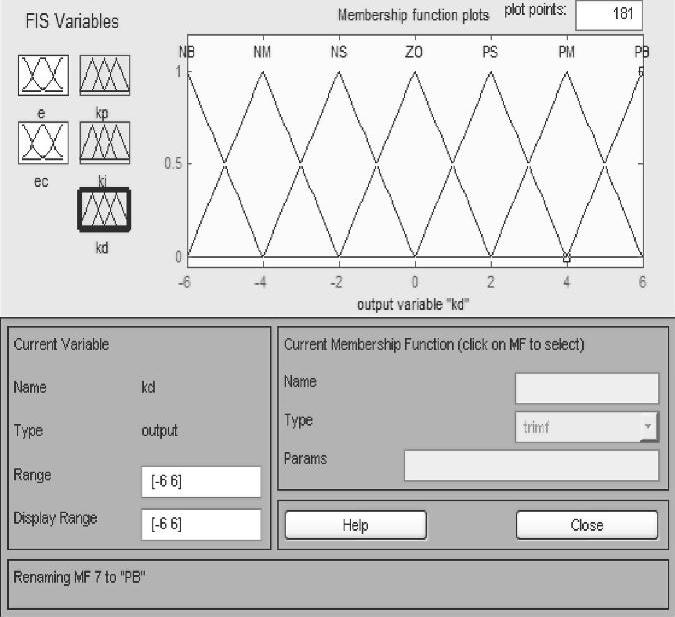
图5-16 整定K_D隶属函数曲线

根据上述隶属函数曲线，得出以上各个变量对应的隶属函数赋值，见表5-5～表5-9。

表5-5 倾角偏差e隶属函数赋值

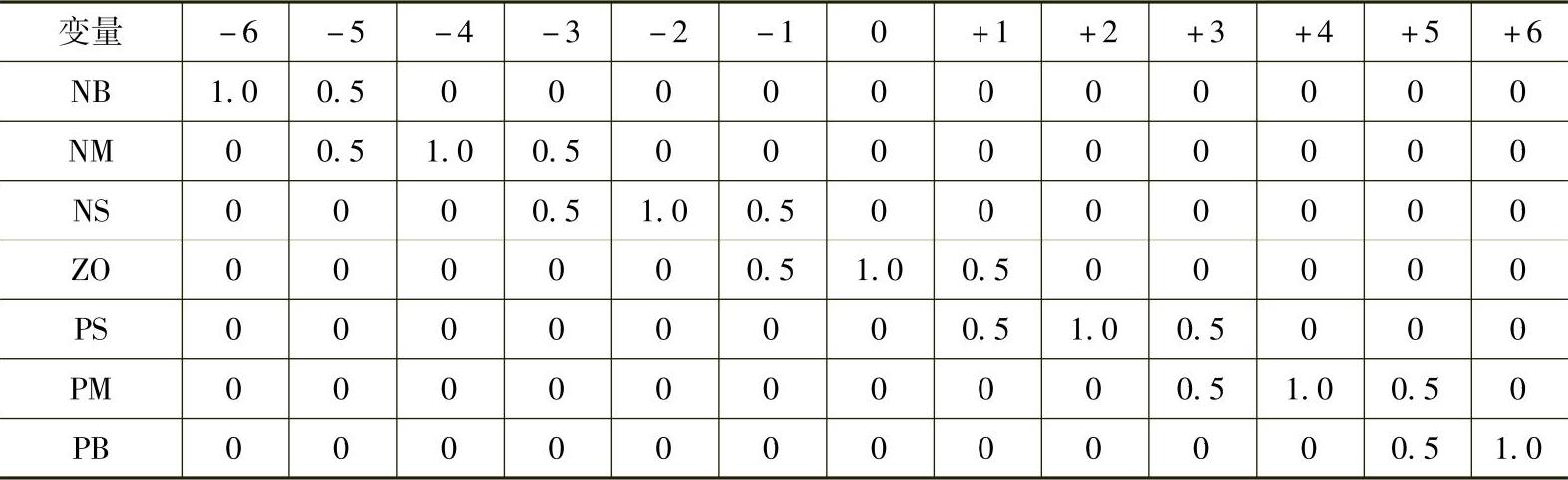
表5-6 倾角偏差变化率e_c隶属函数赋值

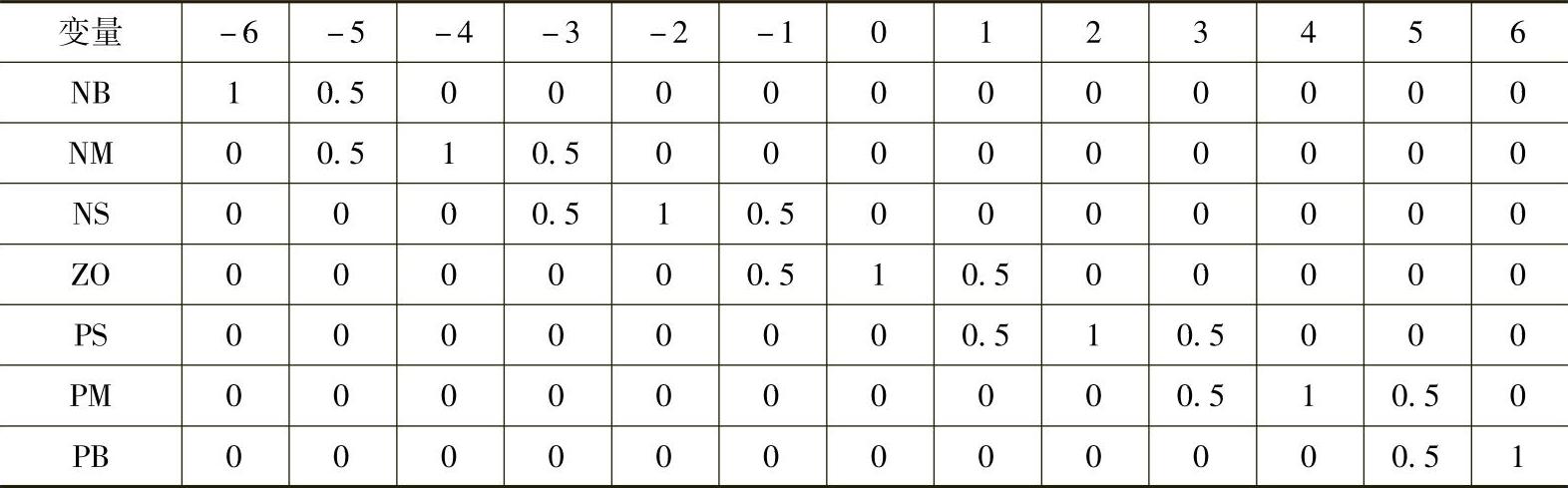
表5-7 比例系数K_p隶属函数赋值

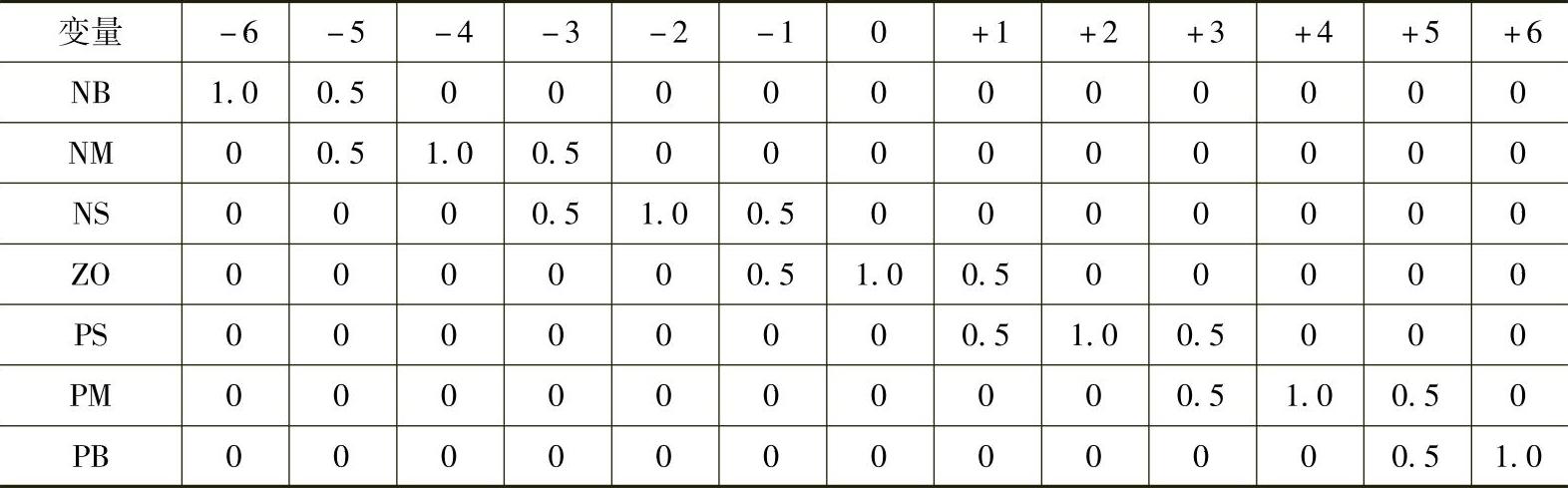
表5-8 积分系数K_I隶属函数赋值

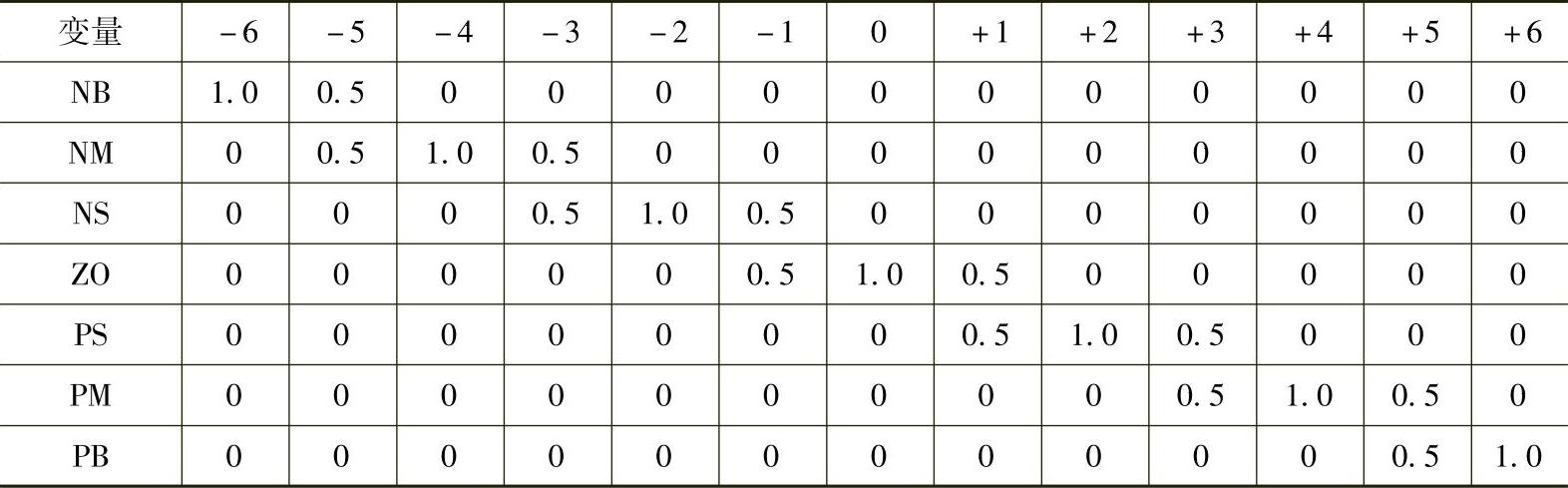
表5-9 微分系数K_D隶属函数赋值

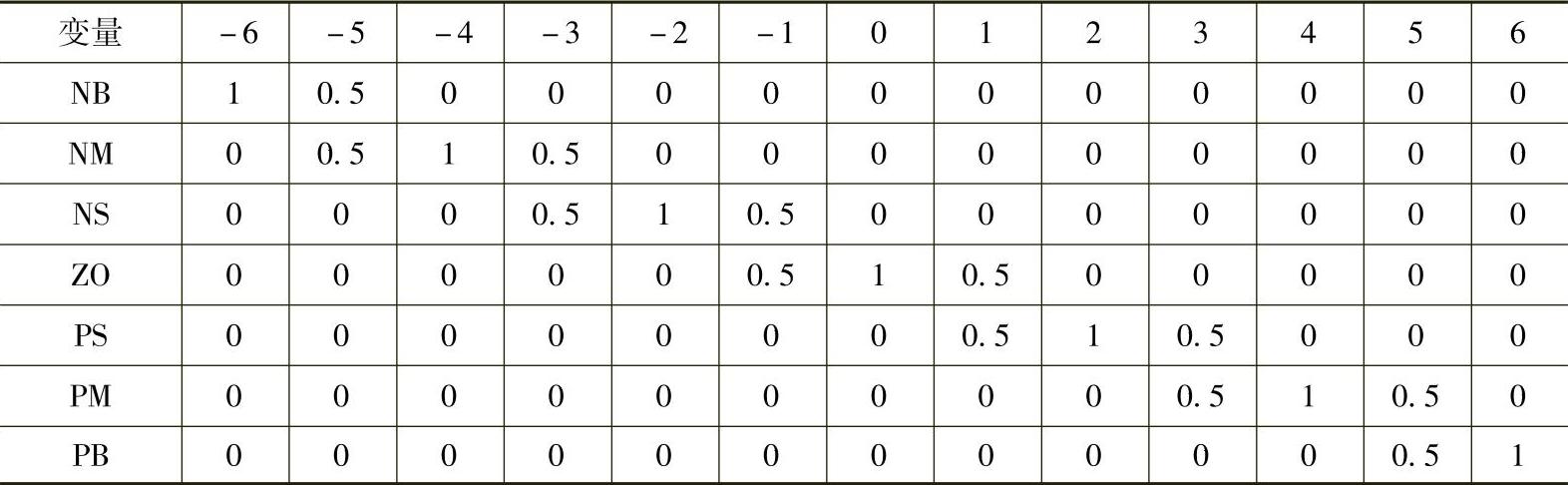
（2）系统模糊规则的确定 模糊控制规则是模糊PID控制的核心部分。模糊控制规则一般由有经验的操作实践者或者由相关的理论专家进行制定。模糊控制理论的整定规则为：

1）实际量与预设量存在偏差过大，此时不考虑e_c变化，为了减少两个变量间的差距，需要选取较大的K_P比例控制系数来加强比例控制，将K_I的值选为零来避免出现积分饱和，而参数K_D的选取则根据干扰情况而定。

2）可以采用参数e和e_c之间的符号关系判断误差的变化趋势，当两个参数保持正负相同的符号，则误差的真实值将被逐渐拉大。此时，需要选取较大的K_P比例控制系数降低过大的绝对误差e，而K_I和K_D参数可根据实际情况选取较小值，进而保证控制器的稳定性和动态性；当e的绝对误差降低到一定范围内，选取中度控制参数K_P、较大的K_I和较小的K_D参数的一般控制方式，控制重点是抑制误差的发展，提高控制器的稳态性。

3）当参数e和e_c处于正负相反情况时，则误差的真实值将被逐渐缩小。此时，需要选取中度的K_P比例控制系数的一般控制以降低过大的绝对误差e，而K_I和K_D参数可根据实际情况选取较小值，进而保证控制器的稳定性和动态性；当e的绝对误差降低到一定范围内，选取中度控制参数K_P、较大的K_I和较小的K_D参数的一般控制方式，控制重点是抑制误差的发展，提高控制器的稳态性，避免系统出现控制震荡。K_P、K_I、K_D模糊规则见表5-10～表5-12。

表5-10 K_P模糊规则表

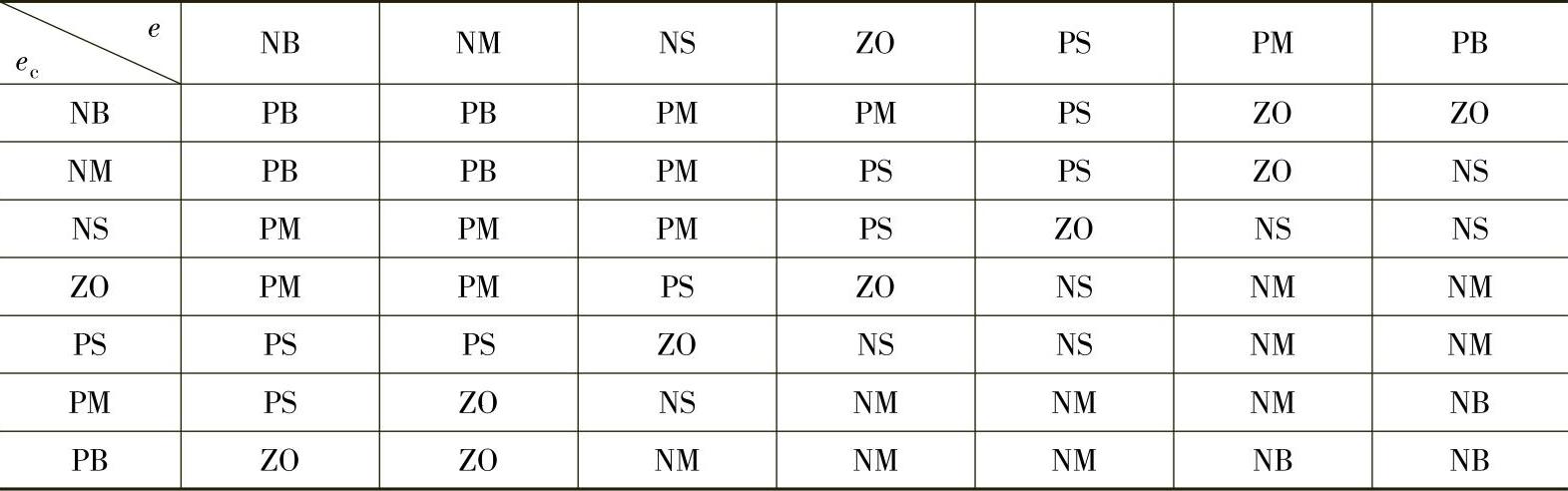
表5-11 K_I模糊规则

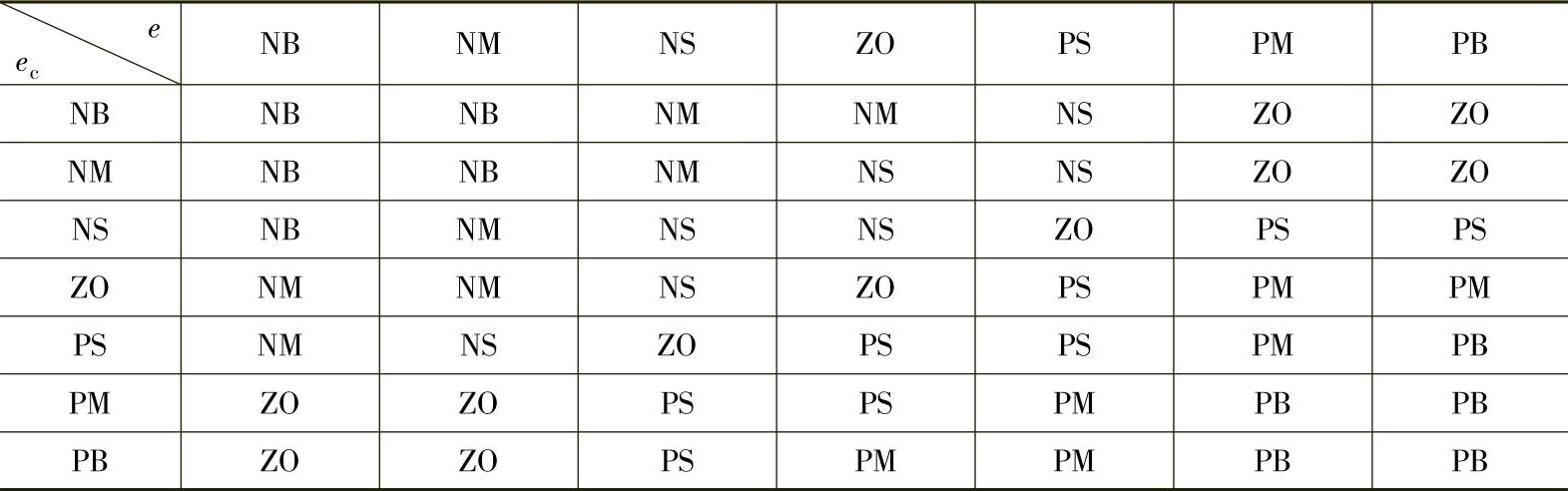
表5-12 K_D模糊规则表

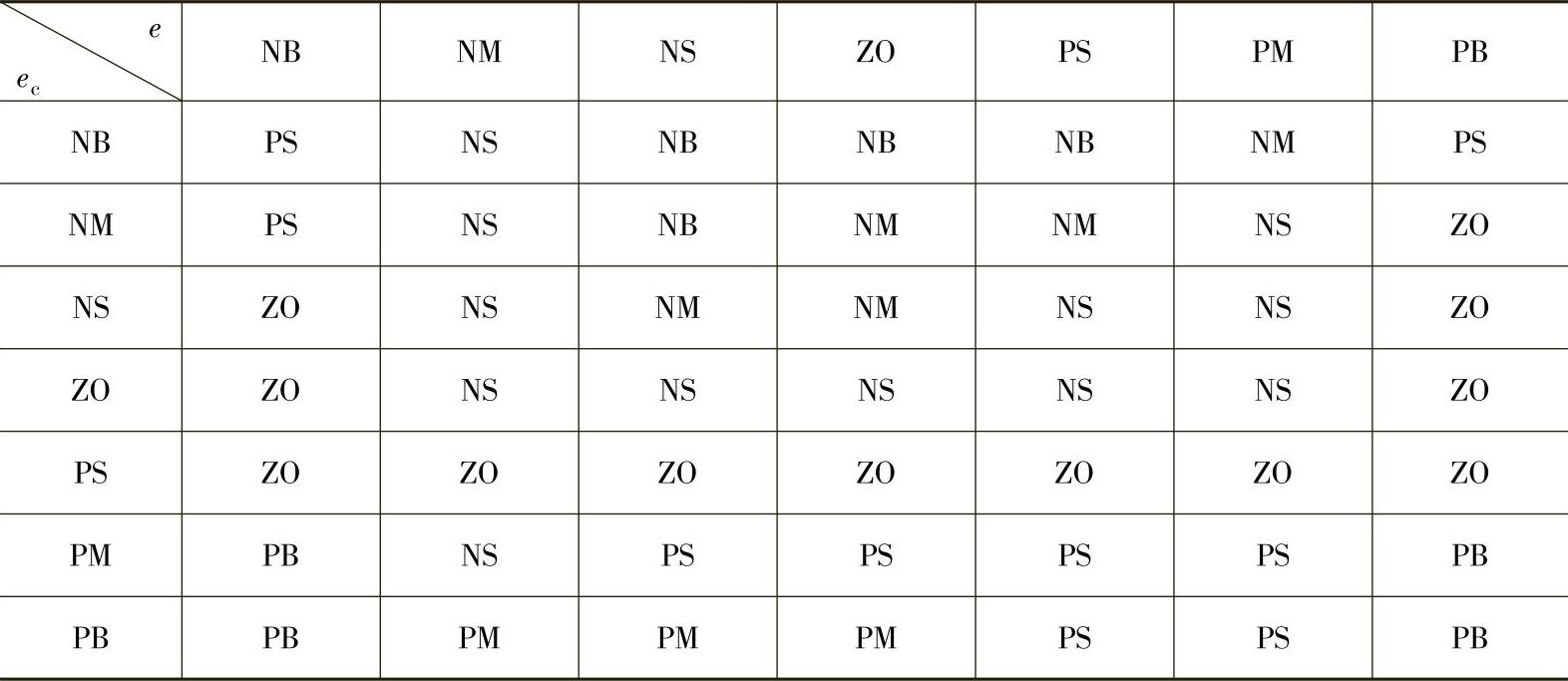
在Matlab中，将模糊规则关系的表述为形式如“ifEandEcThenU”的自然语句形式，用此来表述输入和输出之间的对应关系。完成上述模糊控制规则整定后，根据上述3个模糊规则表将e和e_c输入到Matlab的模糊控制器的规则库里，最终得到了K_P、K_I和K_D的49条规则。运用Matlab将上述模糊规则整定，如图5-17所示。

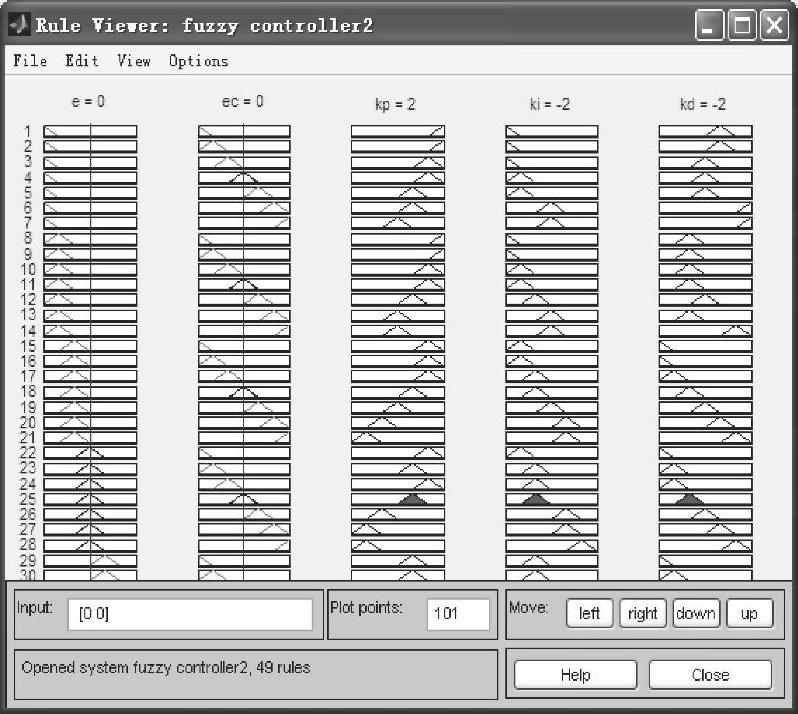
（3）系统参数的解模糊 对Matlab中的模糊控制器进行解模糊算法设定。设定模糊类型为Mamdani型，连接词and对应项设定为min，连接词or对应项设定为max，推理方法设定为min，合成方法设定为max，精确化方法设定重心法。设定完毕后，Matlab中的模糊控制器即已构建完整，通过模糊化、模糊推理和精确化过程后，即可得到模糊结果，任一结果的具体数值均可在Matlab中的规则观测窗中查询。模糊规则观测窗如图5-18所示。

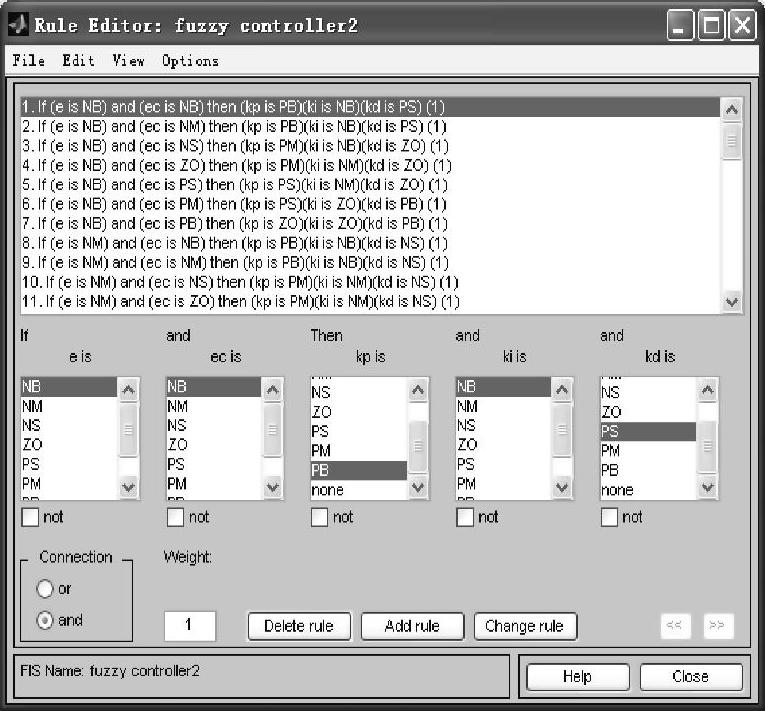
图5-17 Matlab模糊规则整定图

(www.daowen.com)

图5-18 模糊规则观测窗

根据模糊规则观测窗中的数据，当e为-0.636、e_c为1.11时，经既定模糊规则推理，且经重心法反模糊化得出K_P、K_I和K_D的值分别为-0.135、0.135和-0.914。由此可以得出K_P、K_I和K_D经反模糊化后的对应参数。

由Matlab模糊控制器的可视输出可得K_P、K_I和K_D各自的输出三维图，分别如图5-19～图5-21所示。

根据规则观测窗和K_P、K_I、K_D的输出三维图可得K_P、K_I和K_D的模糊查询表，模糊查询表是根据模糊处理规则进行模糊运算的核心部分，模糊查询表直接决定系统模糊化是否成功，其模糊查询表见表5-13～表5-15。

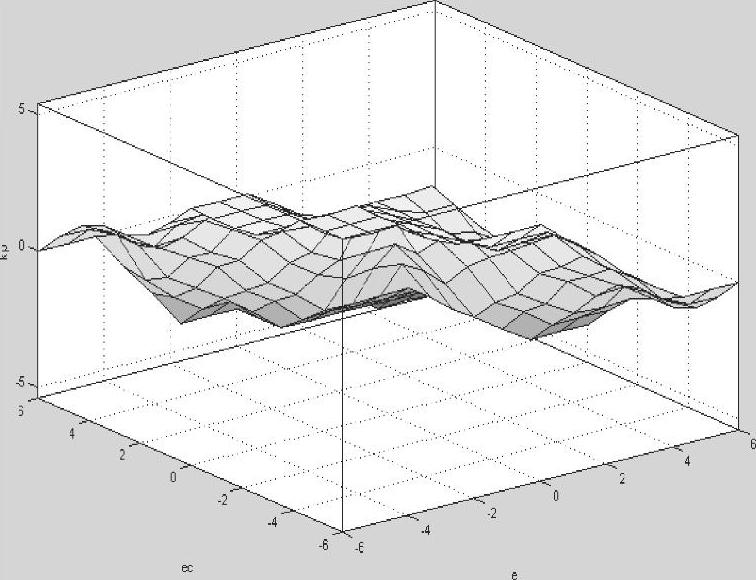
图5-19 K_P输出显示三维图

图5-20 K_I输出显示三维图

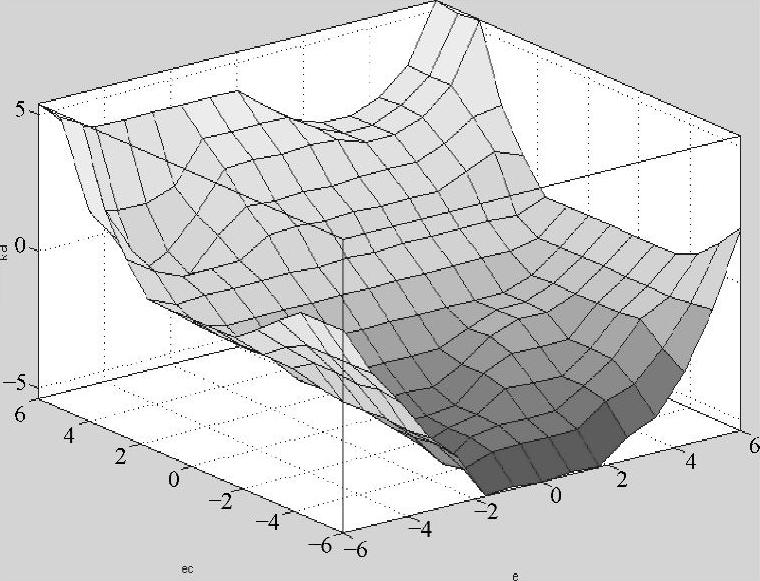
图5-21 K_D输出显示三维图

表5-13 K_P模糊查询表

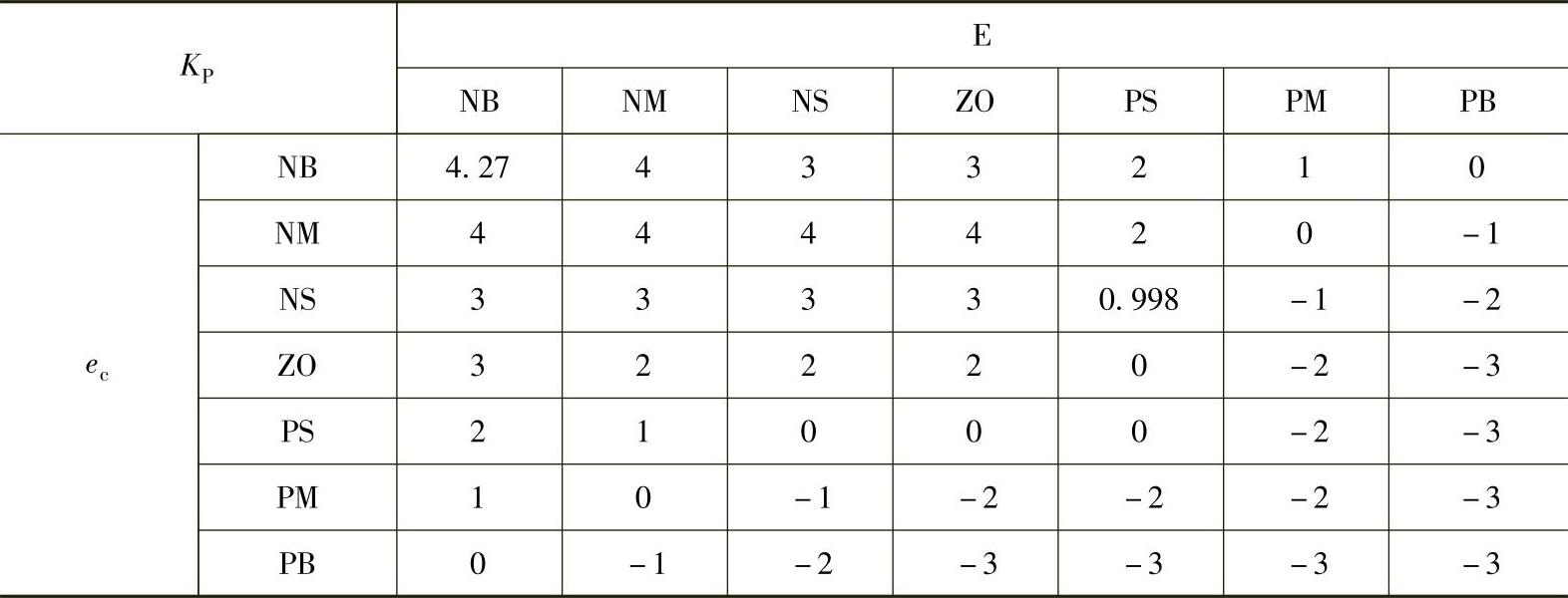
表5-14 K_I模糊查询表

表5-15 K_D模糊查询表

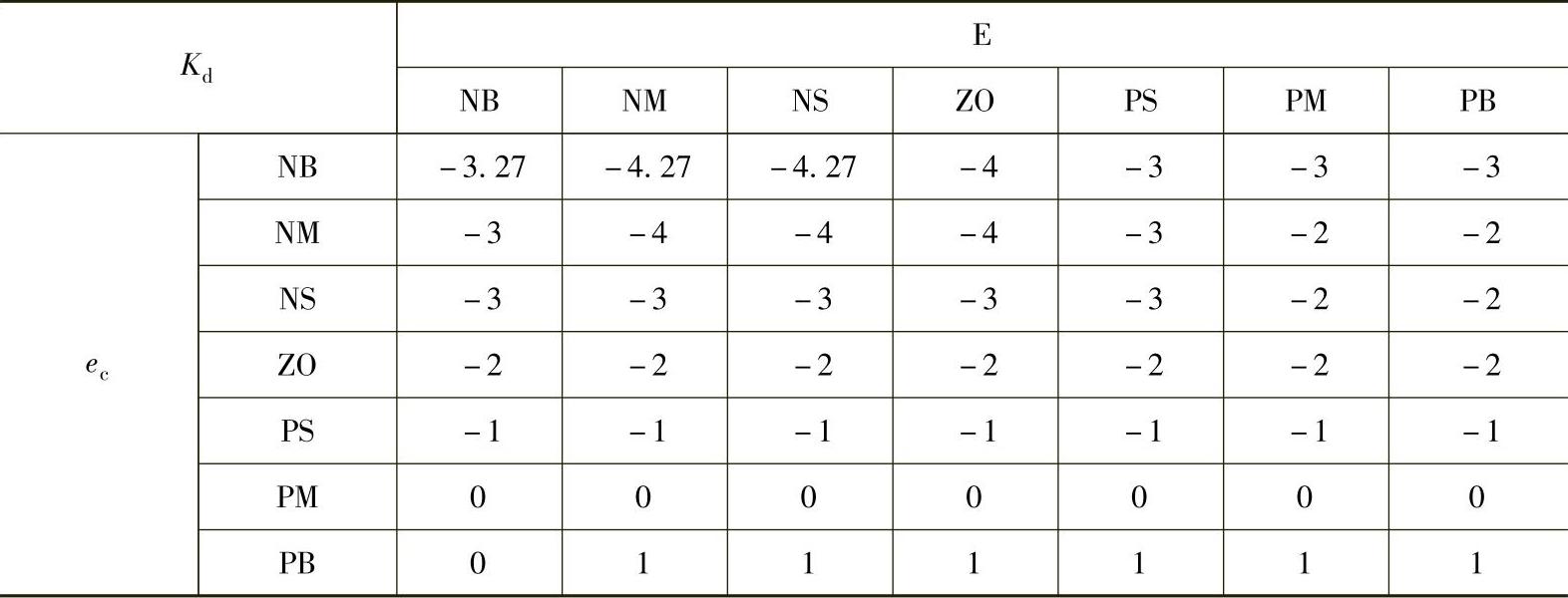
对于不同的e和e_c，首先在上述对应的K_P、K_I和K_D模糊查询表中查询出K_P、K_I和K_D对应的具体增量值；而后，得到的具体增量值再乘以对应的比例因子得到其实际值；最后，将得到的实际值代入式（5-11）中，即可完成对参数的自动整定。

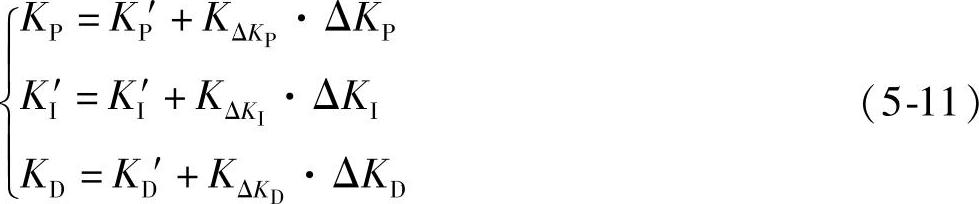
式中 K_P、K_I、K_D——模糊PID控制器的三个输出参数；

K_P′、K_I′、K_D′——模糊PID控制器的三个初始参数；

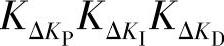
——模糊PID控制器三个参数所对应的比例因子，其中，，。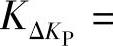

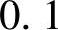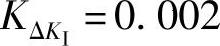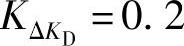运用Matlab软件中的fuzzy模块完成高空作业平台的自动调整系统的模糊PID控制器的构建。运用此软件进行了精确量的模糊化、模糊规则整定和反模糊化的工作，Matlab中模糊PID控制器的总体结构如图5-22所示。

3.模糊PID控制器与传统PID对比分析

为了对上述所制定的模糊PID调整控制算法进行分析验证，运用Matlab中的Simulink模块库对本算法进行仿真分析。Simulink模块库中有很多工具箱以适用于对不同系统的仿真分析。本系统仿真所运用的主要工具箱有：Simulink基本及扩展工具箱和Fuzzy logic（模糊逻辑）工具箱。Simulink中的fuzzylogic工具箱中有Fuzzy模块（模糊推理系统编辑器）、Mfedit模块（隶属度函数编辑器）、Ruleedit模块（模糊规则编辑器）、Surfview模块（模糊推理输入输出曲面视图）四个模块，在算法整定中即运用上述模块完成模糊PID调整算法的整定。

Simulink环境中打开仿真模型编辑环境窗口，将仿真所需要的模块用鼠标拖入并连接好，建立仿真模型。本系统运用Fuzzylogiccontroller模块实现模糊推理判定，同时此模块要与上文中模糊控制箱进行连接才能完成仿真。上节建立的模糊-PID控制器的仿真模块如图5-23所示。

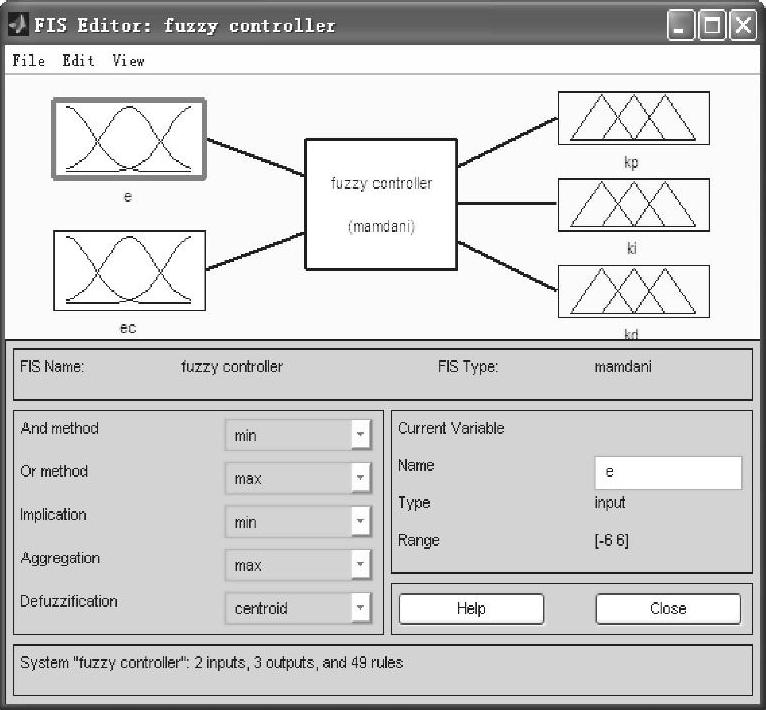
图5-22 Matlab中模糊PID控制器的总体结构图

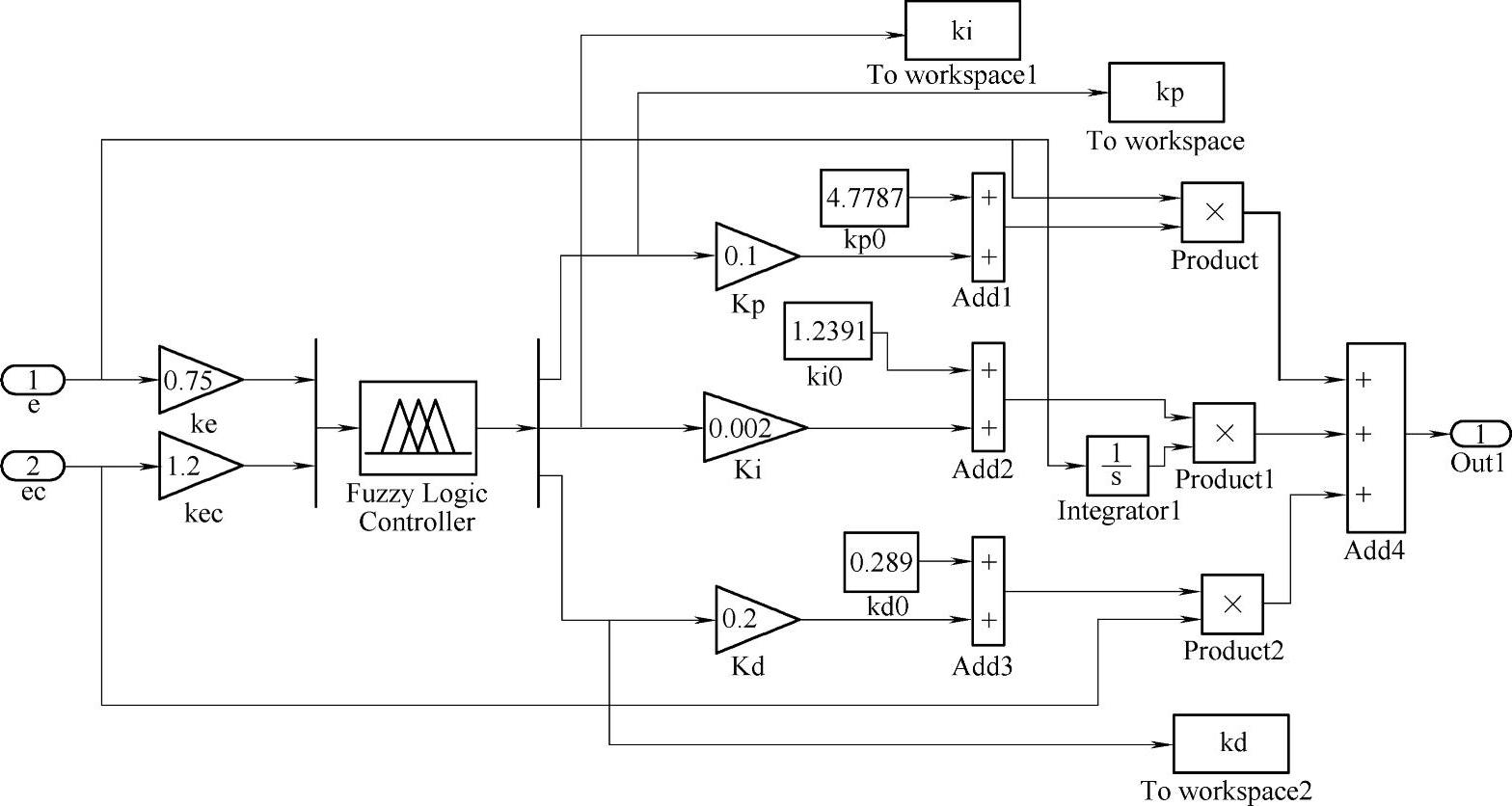
图5-23 模糊-PID控制器的仿真模块

在仿真中对此模糊-PID控制器做了封装，本封装模块为fuzzy-PIDcontroller，为一个两输入、单输出的系统。其内部封装着上述的模糊-PID控制器，其完成上述控制器的全部功能，其封装模块如图5-24所示。

图5-24 模糊-PID控制器封装模块

对应用该模糊-PID控制器的高空作业平台的调整系统进行了仿真，同时仿真过程中也对加载了单一的应用PID控制策略的高空作业平台进行了仿真。本仿真系统中加装了干扰模块，以便分析测试本模糊-PID调整算法的抗干扰能力。仿真模块图如图5-25所示。

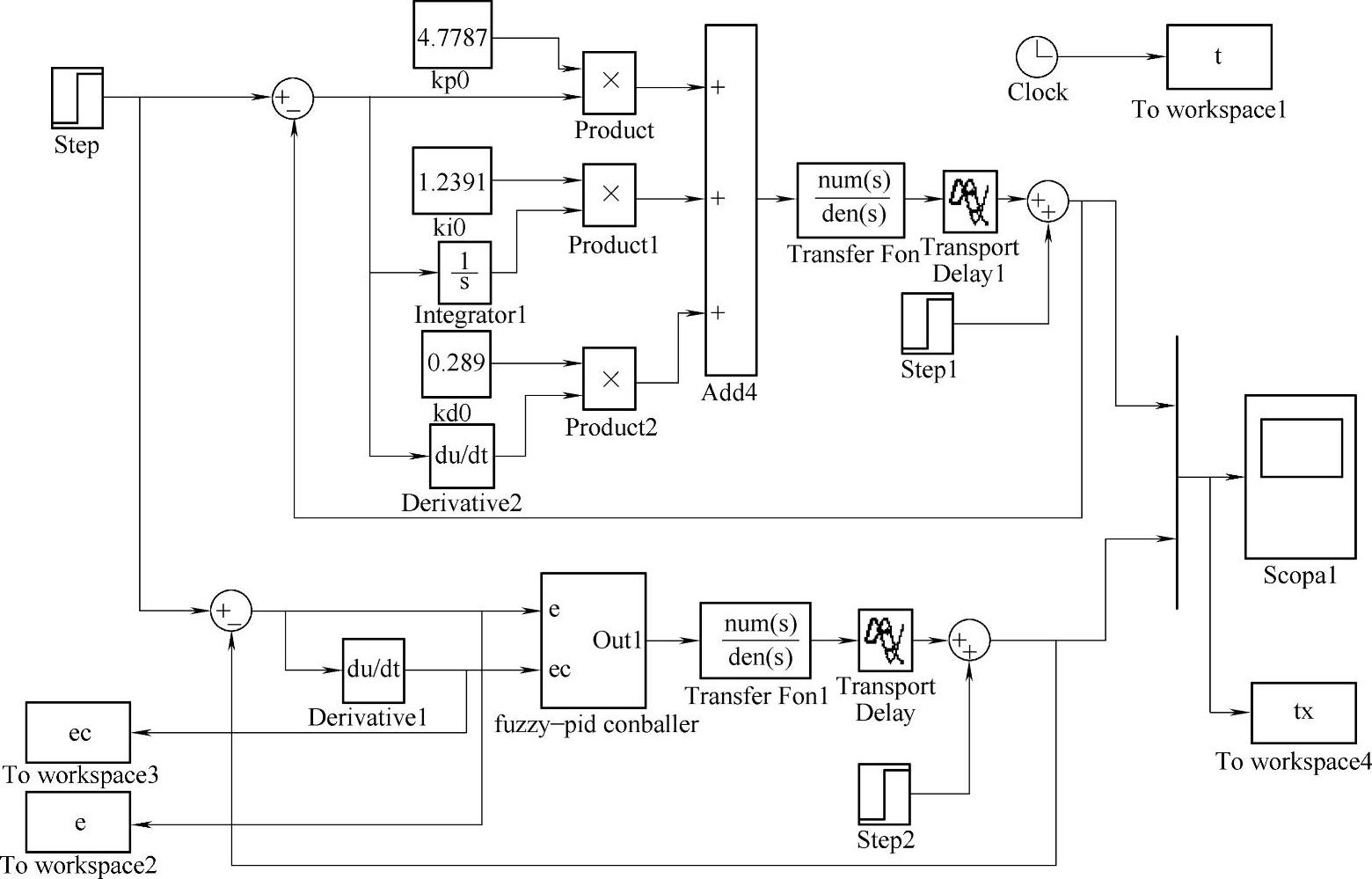
图5-25 仿真模块图

本仿真系统的仿真时间为5s，采样频率设置为0.01s。仿真过程首先测试模糊-PID调整算法和单一PID调整算法的阶跃响应，而后在1.5s的时候给系统的负载端加入一幅值为1的阶跃干扰，以分别测试对比两个算法的抗干扰能力和稳定性。模糊-PID的初始PID控制参数及单一的PID调整算法的控制参数均为K_P′=407787、K_I′=1.2391、K_D′=0.269。此参数通过Ziegler-Nichols整定方法获得。本系统的控制对象为一个三阶传递函数为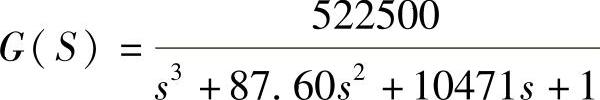。通过仿真分析得出，系统的模糊-PID和PID阶跃响应曲线如图5-26所示，模糊-PID和PID抗干扰特性曲线如图5-27所示。

由图5-26可以得出采用模糊-PID调整算法的系统在系统的上升时间、峰值时间、最大超调量、调整时间、震荡次数及稳态误差等各项指标均优于传统的单一PID控制算法。可得采用模糊-PID控制算法控制的响应时间在0.5s以内，传统PID控制算法的响应时间在1.5s左右，模糊-PID控制算法的响应时间大大缩短。图5-27中，在同样1.5s时刻上加负载干扰，采用模糊-PID控制算法的系统恢复稳定的效果明显比传统单一PID控制算法系统要好，由此得出模糊PID控制算法的抗干扰能力优于传统PID控制算法。

为对模糊PID算法有更全面的分析，对模糊PID算法中的误差、误差变化率和ΔK_P、ΔK_I、ΔK_D的输出等参量进行了实时监测。模糊-PID整个过程的误差变化曲线、误差变化率曲线和ΔK_P、ΔK_I、ΔK_D的输出变化曲线分别如图5-28～图5-32所示。

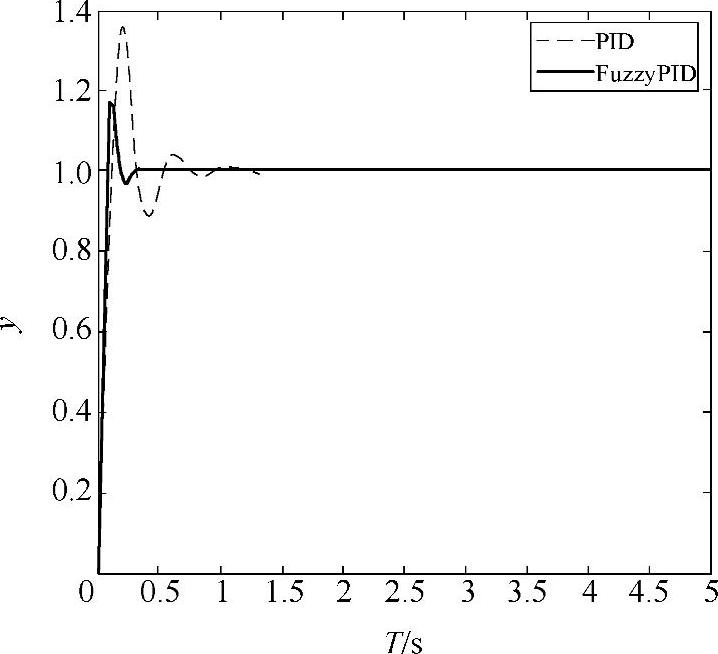
图5-26 模糊-PID和PID阶跃响应曲线

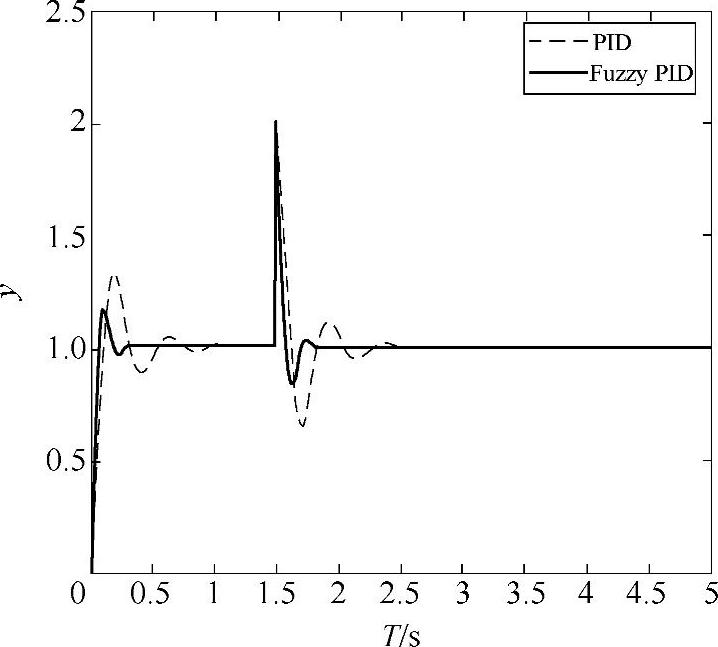
图5-27 模糊-PID和PID抗干扰特性曲线

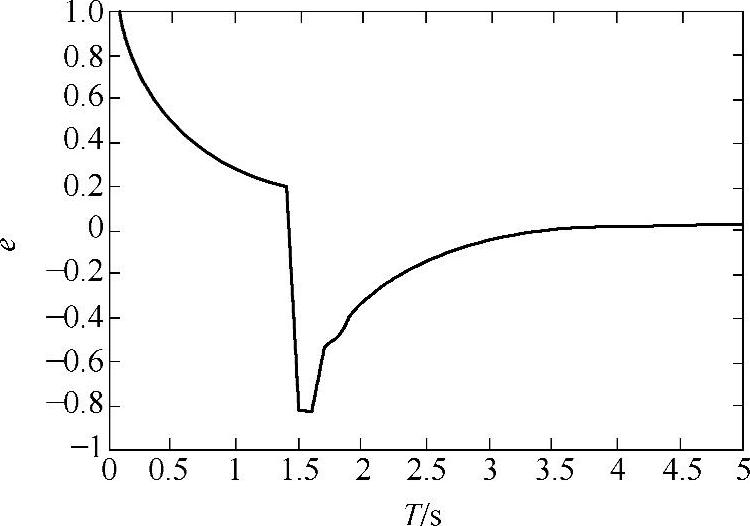
图5-28 误差变化曲线

图5-29 ΔK_I输出曲线

图5-30 ΔK_P输出曲线

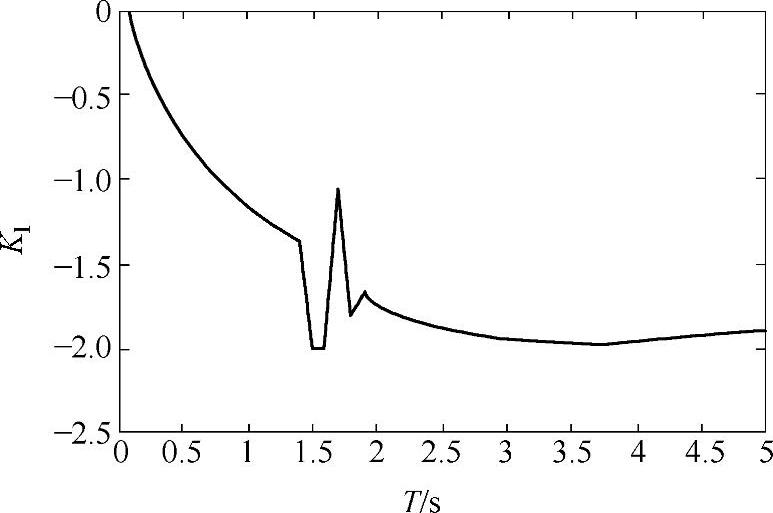
图5-31 误差变化率曲线

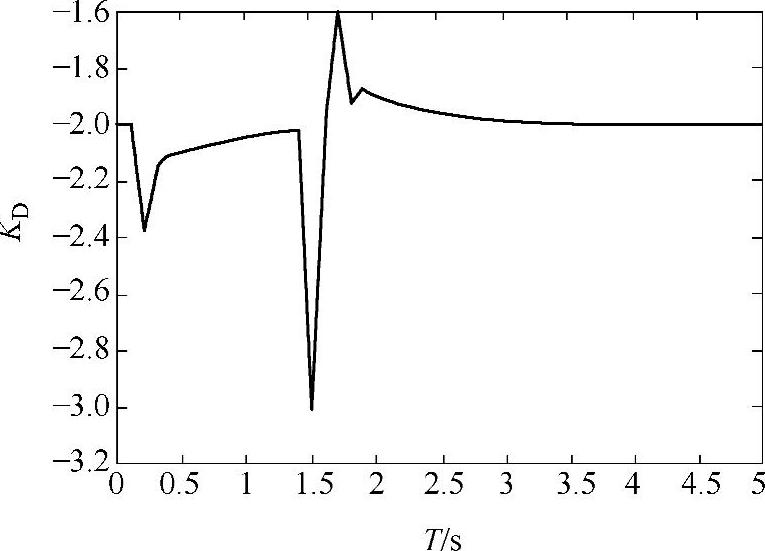
图5-32 ΔK_D输出曲线