1.摩擦传动力学方程的建立

截取钢丝绳为研究单元完成其作用力研究。图4-30所示为钢丝绳单元体受力分析图，为减少模型计算量，研究中给定确切的钢丝绳的摩擦因数，并忽略弯曲刚度及惯性的变化，将钢丝绳结构看做线弹性材料。

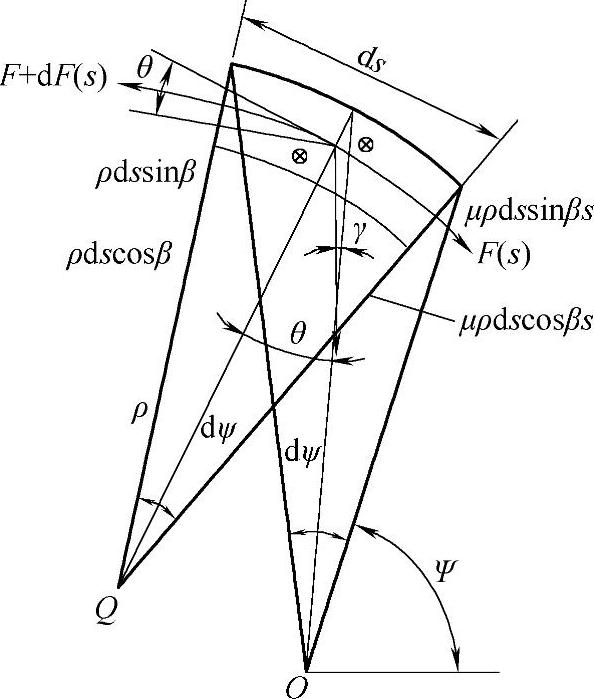
图4-30 钢丝绳单元体受力分析图^[40]

钢丝绳受力单元在圆周方向上的受力平衡方程

dF+2pdssinβsinθ-2μpdscosβ_ssin（θ+γ）=0 （4-61）

单元在径向上的受力平衡方程

-Fdψ+2pdssinβsinθ-2μpdscosβ_ssin（θ+γ）=0 （4-62）

引入径向曲率关系式ρ=ds/dψ，可将方程改写为

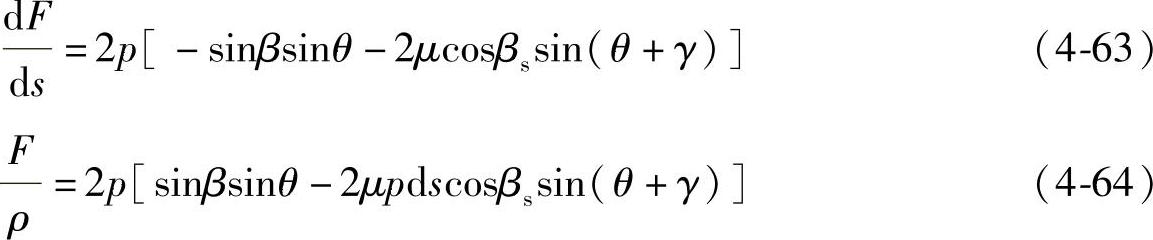
式中 F——绳索的拉力；

p——绳索与绳轮间的接触面的正压力值；

β——绳轮与钢丝绳配合的参数；

θ——钢丝绳的在绳轮上的包角；

γ——钢丝绳传动中的滑动角；

β_s——滑动平面的楔形角，下标s表示指定坐标系下的参数；

μ——摩擦因数的计算值。

在传动力的作用下，钢丝绳在绳轮表面会发生微动滑移，这对钢丝绳传动的角速度ω、和速度v_r、绳轮速度rω均产生相应的影响。分析过程中，钢丝绳的速度可以通过绳轮的速度矢量和滑动速度的矢量共同构成。因此在圆周方向和径向上分别可以给出下面的关系式

v_rcosθ=rω+v_ssinγ （4-65）

v_rsinθ=v_scosγ （4-66）

联立式（4-65）、式（4-66），可以得到滑动角的正切值

钢丝绳摩擦传动中速度随钢丝绳拉力F的变化发生相应的变化，其大小为

v_r=F（1+ε） （4-68）

若将钢丝绳看作为线弹性材料，则钢丝绳整体轴向应力和应变之间满足线性关系

F_a=Kε （4-69）

式中 K——弹性系数。

钢丝绳在径向作用力F/ρ的作用下发生变形可以通过公式和钢丝绳本身受力变形进行研究，由于钢丝绳在摩擦传动工作过程中单侧半圆周面受压力p作用，使钢丝绳整体变扁，具体形状的变化还与绳轮中绳槽的形状有关。

如图4-31所示钢丝绳摩擦传动绳轮中绳槽的径向深度为x，拉力在绳轮槽壁的压力为p_x，考虑径向刚度系数k得到

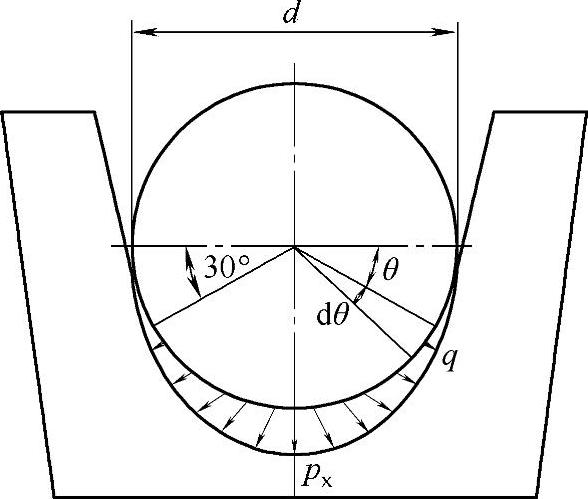
图4-31 钢丝绳对绳轮的垂直作用力分析图

轴向载荷可以分解为

p_x=p（cosβ+μsinβ_s） （4-71）联立上面两个公式得到

根据绳轮截面的几何关系，可以将笛卡儿坐标转换为极坐标，对钢丝绳微元有

式中 θ——可以通过式tanθ=dr/（rdφ）=r′/r进行换算。

通过图4-32获取到dψ=dφ-dθ，结合式（4-73）可以得到

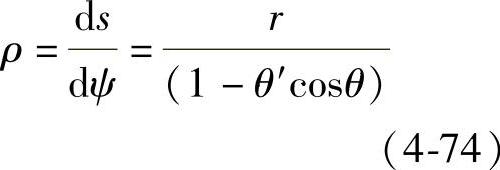
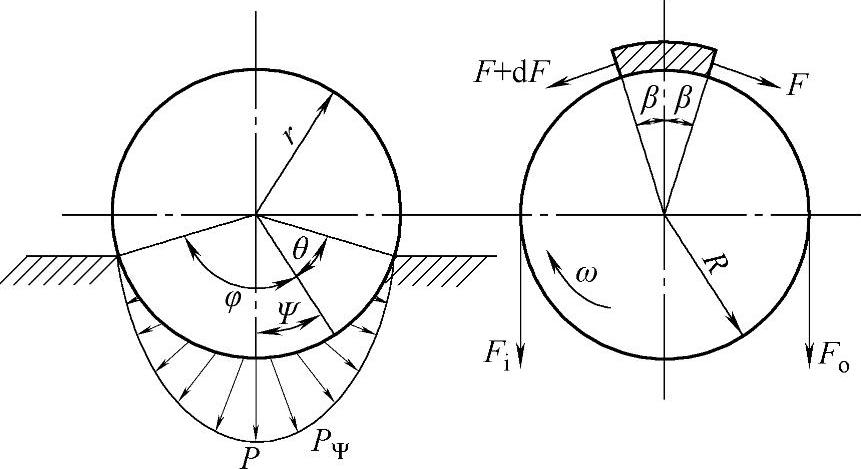
图4-32 绳槽受力截面分析图

将钢丝绳绳轮的旋转坐标面与绳轮轮缘坐标面进行变换得到

tanβ_s=tanβcosγ （4-75）

将上述方程进行整理，结合钢丝绳绳轮的几何关系得到

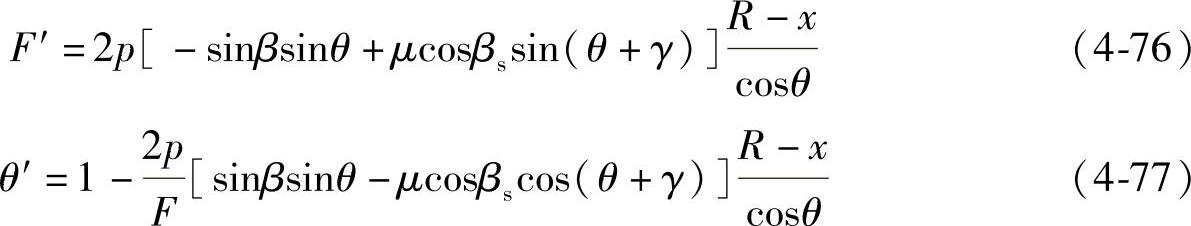
结合tanθ=dr/（rdφ）=r′/r，及几何关系x=R-r得出

x′=-（R-x）tanθ （4-78）

通过给出的三个微分方程及三个几何方程，得到了钢丝绳绳轮摩擦传动力的计算模型，模型中存在待定未知参数F、x、p、θ、γ和β_s，结合绳轮绳槽的几何形状可解出三个独立变量方程。

2.摩擦传动力学方程的解

通过研究提出了钢丝绳摩擦传动的力学方程，并且结合摩擦理论的发展给出具体计算模型，通过计算给出了用于判断摩擦接触力和相应应变的数据。由于钢丝绳内部摩擦的作用，钢丝绳摩擦传动过程对钢丝绳直径变化的影响可由一个标准函数表示。提出获取钢丝绳等效摩擦因数的精确方法，计算给出预测各种摩擦传动行为更为有效的参考。

如图4-32所示为钢丝绳在U型绳槽内摩擦传动的稳态运行，该钢丝绳传动主要的系统参数有钢丝绳进入端和离开端拉力值F_i和F_o，绳轮直径R，绳槽槽底弧半径R_h，槽内楔形角β，绳轮与钢丝绳间的摩擦因数μ，绳轮角速度ω，钢丝绳的弹性模量E，钢丝绳径向弯曲刚度k，单位长度密度为m_i（s）。

将悬吊式作业装备型号为PLZ800提升机构的相关数据作为原始数据，进行方程计算，摩擦传动系统的计算参数给定为F_o=1×10³N，F_i=1.6×10⁵N，f_o=0.45，k_o=55MPa，A_i=45mm²，E=2.10×10⁵MPa，R=180mm，R_h=158mm，β=13°，μ₀=0.3。

综合利用上述参数及所推导公式，可计算出绕在摩擦绳轮上的传动钢丝绳中拉力的变化规律，如图4-33所示。图中虚线为利用欧拉公式计算所得的拉力变化规律。

按照欧拉公式计算结果，理论上分析在未出现滑动之前，拉力F为常数，等于最大提升作用力F_imax；摩擦出现滑动时，摩擦轮提供钢丝绳拉力F按指数规律减小。按本节式（4-60）给出的计算方法，可得出钢丝绳绳轮工作提升拉力随绳轮包角的变化关系图，该变化首先体现在钢丝绳自身的变形。在接近摩擦传动滑动临界点时，变化趋势明显，经过临界区域后，由于滑动摩擦因数与静摩擦因数的关系，使作用力变化趋势变得缓慢。此外，当考虑钢丝绳的弹性变形时，发生相对滑动的临界点会比用欧拉公式所得的临界点稍迟。传统的弹性滑移率计算方法在对钢丝绳摩擦传动计算时不能准确地反映实际趋势，计算方法修正后提升力的变化趋势得到了明显改善。

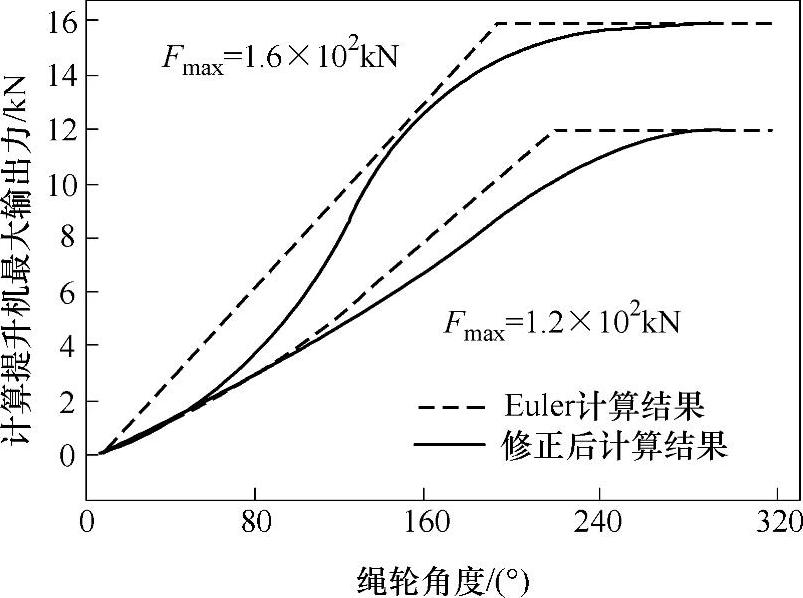
图4-33 提升拉力与绳轮包角间的变化规律

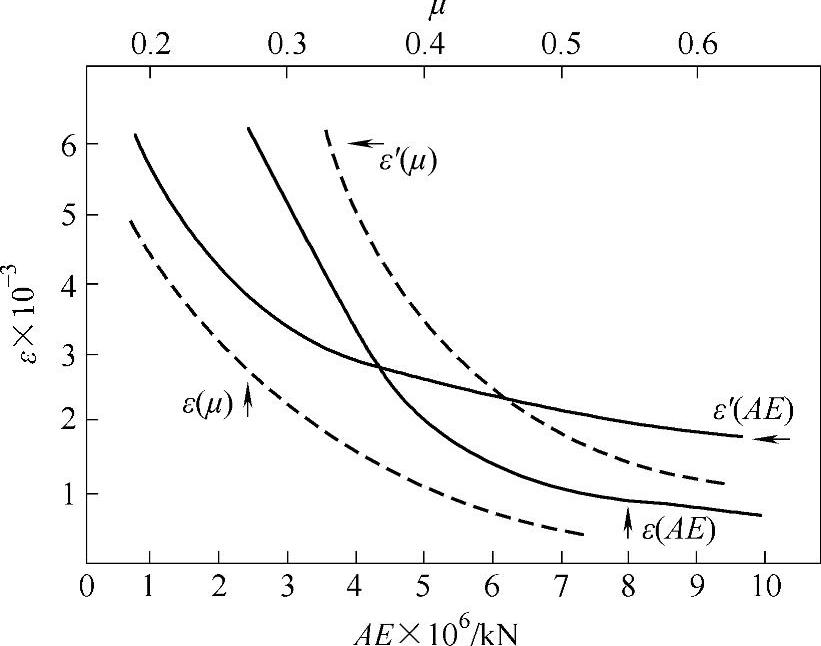
图4-34 弹性滑移率ε和滑移率ε′的变化规律

根据AE和μ的变化可以作出钢丝绳摩擦过程中弹性滑移率的变化曲线，如图4-34所示，当进入端和离开端间的作用力之差一定时，若传动钢丝绳磨损程度较小、弹性较好，即弹性模量E减小，则滑移率ε和ε′增大；反之，ε值减小，甚至趋近于0。当ε值趋近于0时，说明在作用力之差较小时，传动钢丝绳与绳轮之间没有弹性滑动，这不符合实际情况。经过修正后的滑移率ε′如图4-34所示，当AE逐渐变大时，ε′趋近于定值，这样的结论相对较符合实际；同时图4-34给出了滑移率与摩擦因数间的相互关系，摩擦因数越大，滑移率ε和ε′越小，修正后ε′适合于摩擦因数在0.32～0.63范围变化，这也较好地与实际情况吻合。

钢丝绳摩擦传动计算过程中，需要确定钢丝绳与绳轮接触的边界条件。为了保证钢丝绳摩擦传动稳态运动方程有解，在实际确定上述边界条件时需将钢丝绳与绳轮接触区域的未知边界条件转化成特定范围内的标准边界值进行处理。

(www.daowen.com)

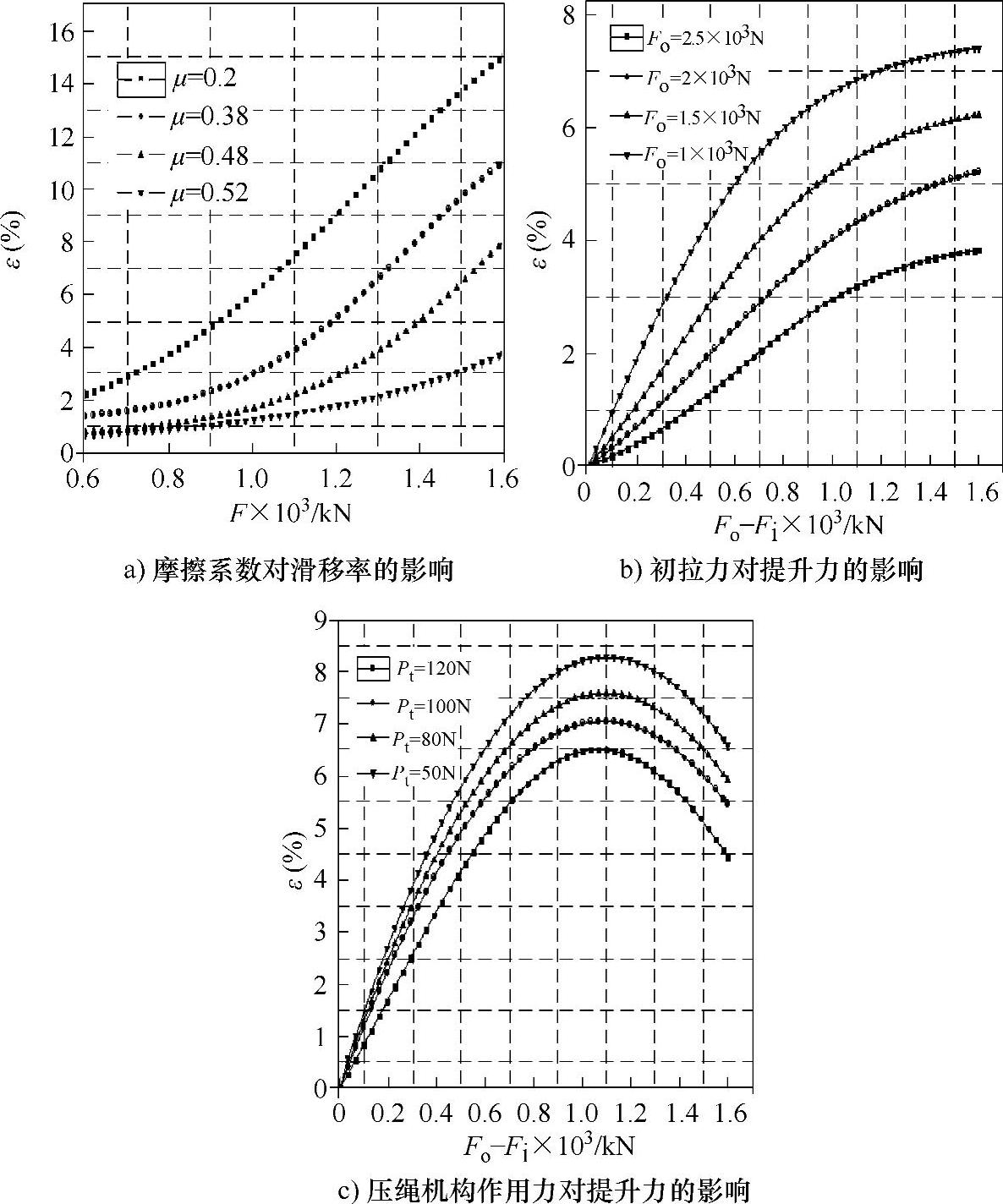
图4-35 各参数影响下摩擦提升能力与滑移率间关系

图4-35给出了不同参数条件下系统提升力与滑移率间的关系曲线。首先，在没有初拉力的情况下，计算得到摩擦因数对提升能力的影响关系。从图4-35a中可以看出提升机构的摩擦因数的提高可以减小滑移率，在提升机输出较小时，这种区别并不明显，随着提升力的加大，摩擦因数对滑移率改善更为明显。图4-35b为将摩擦因数_μ=0.38设为固定值，改变提升系统的初拉力F₀分别为1000N、1500N、2000N和2500N，计算数据表明适当地提高系统的初拉力可以有效地改善提升能力，但实际工作中初拉力过大可能引起摩擦力降低甚至损害钢丝绳。图4-35c所示为计算摩擦绳轮上采用压绳机构后对钢丝绳与绳轮间压力的增大量，从图中可以看出其作用效果与改变提升初拉力效果类似，但在大提升力状态下其滑移率开始降低、对摩擦效果的改善更为突出。

3.提升机构传动性能测试与分析

摩擦钢丝绳受力变形量是影响提升性能的主要因素，变形量本身又受到许多因素影响，但钢丝绳在实际的使用过程中，表现出的特性并不复杂。对提升系统进行测试前，首先通过拉伸钢丝绳（4∗31SW+PP8.6，右捻向镀锌）得到试验钢丝绳在拉伸过程中加载和卸载的应力与应变曲线，如图4-36所示。

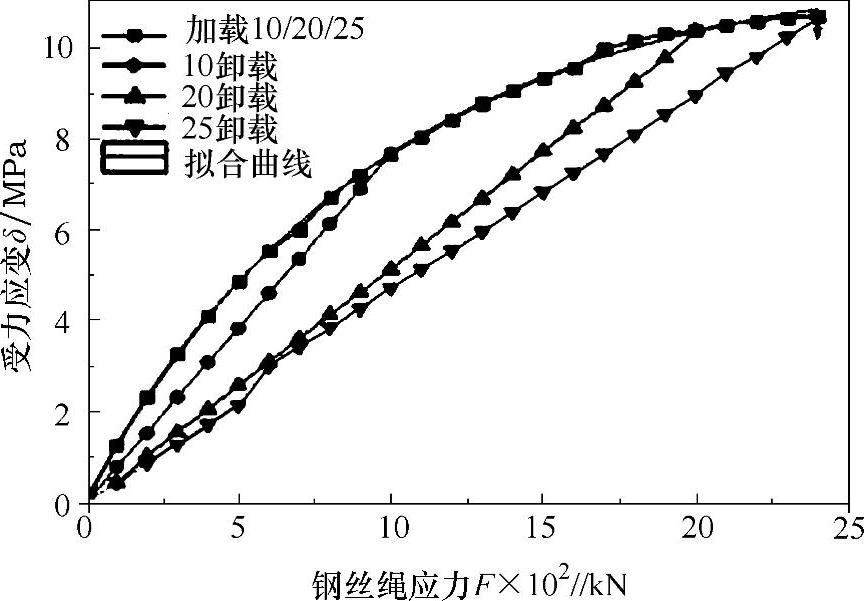
图4-36 钢丝绳应力与应变曲线

试验过程对钢丝绳进行了三次加载拉伸和卸载，钢丝绳加载时，拉伸应力分别从零缓慢增加到1.0×10³kN，随后进行卸载；恢复后再从零加载至2.0×10³kN，随后进行卸载；恢复后再从零加载至2.5×10³kN。测试完成三次加载和三次卸载，卸载时应力逐渐减少至零。所得到的测试数据绘制曲线如图4-36所示，从数据中可以看出三次加载过程中钢丝绳应变曲线重合度较高，三次不同的加载应力使其卸载数据曲线存在较大不同，卸载曲线分别与加载的作用力对应相关。

曲线表明钢丝绳受力过程中，变化规律不符合胡克定律，表现出较为明显的弹性滞后，可以通过方程拟合获取摩擦钢丝绳加载曲线方程的参数。图4-36中给出了加载曲线的拟合参数及数据，拟合方程形式为

δ=A₁exp（-F/t₁）+δ₀ （4-79）

方程为近似表达，存在一定的拟合误差，拟合后可以得到相关参数A₁、t₁、δ₀。

4.摩擦绳轮直径对提升性能的影响

试验采用单体提升机进行研究，设计不同尺寸的提升机摩擦轮，从而获得不同绳轮提供的摩擦力变化。如图4-36所示摩擦轮是摩擦提升机构内的核心部件，与摩擦钢丝绳直接接触提供摩擦力，绳轮的大小和结构直接影响提升能力。从理论分析可以看出，绳轮中心到钢丝绳中心的半径r主要影响钢丝绳在绳轮表面的摩擦力。

从式（4-60）中无法得出绳轮直径对摩擦传动能力的影响，需要采用试验的方法进行更为深入的研究。试验过程中，分别加工直径为18cm、19cm、20cm、21cm、22cm、23cm六种绳轮，同时加工一种S形提升结构摩擦轮，直径为26cm，从动绳轮直径为25cm，如图4-37所示。试验过程组装六台α形提升机和一台S形提升机进行了对比试验，记录拉力不断变化引起钢丝绳摩擦传动的相对滑移量与钢丝绳运行距离比值，计算出对应的滑移率，绘制性能对比曲线。测试过程中振动传感器以秒为单位记录振动信号，温度传感器每2min记录一次提升机机体的表面温度。

图4-37 六种直径绳轮结构图

在测试中，钢丝绳采用镀锌钢丝绳，压绳机构压力按标准设定为175N，压盘式压强为0.29MPa，摩擦绳轮的加工材料为40Cr。试验过程配备不同直径绳轮的提升机进行提升力性能测试，同时检测了提升过程的振动信号及机身温度信号，得出数据绘制相应曲线。通过测试钢丝绳在摩擦过程中的滑移率，并对滑移率进行计算得到了7种不同绳轮直径下提升机的提升能力曲线，如图4-38所示。

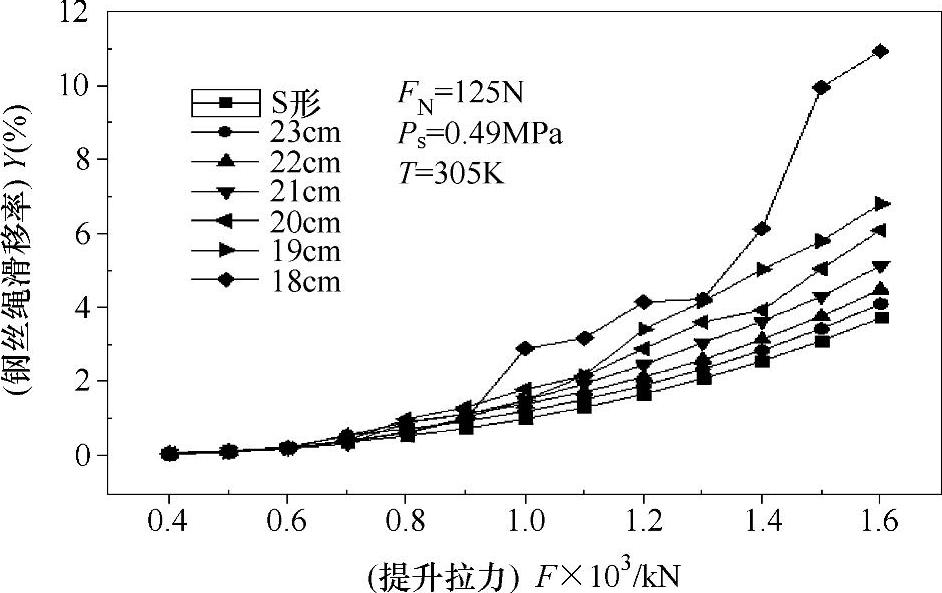
图4-38 不同绳轮直径下提升机的提升能力曲线

从图4-38中可以看出当提升拉力小于0.6×10³kN时，七种绳轮直径下的提升机摩擦传动中出现的滑移率基本相同，当测试提升拉力大于0.6×10³kN后，滑移率的差距开始逐渐变大。其中，S形提升机的提升能力改善明显，在提升拉力为1.6×10³kN时滑移率仅为3.75%，这主要是因为其具有两个摩擦绳轮的结构，并采用绳轮夹紧的压绳方式。在绳轮直径为18cm、19cm、20cm三个提升机的测试中，提升拉力大于1.0×10³kN情况下，提升性能出现的波动较大，波动最大的为18cm直径绳轮的提升机，其滑移率已接近12%，已经无法正常工作。

振动是机械传动的重要考核指标，如何在保证传动要求下降低提升系统的振动，需要在试验中对结构参数进行不断的改进，绳轮直径的改变是否对提升机振动产生影响及产生怎样的影响没有相应的研究报告，这方面的研究较少。为此，本试验在对提升性能测试的同时，采用振动传感器测试提升机自身的振幅变化。图4-39所示为S形提升机的振动曲线，图4-40所示为α形提升机采用不同绳轮直径的振动曲线。

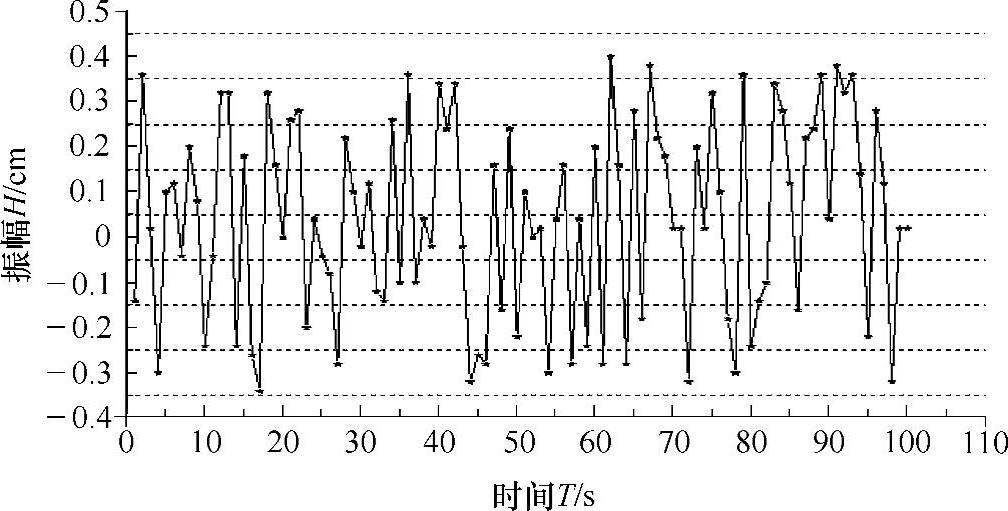
图4-39 S形提升机的振动曲线

对比图4-39和图4-40发现，S形结构的提升机测试中振幅较大，在-0.35～0.4cm之间，而提升机测试中振幅相对较小，可能与压绳机构有关。在α形提升机中随着绳轮直径的增加，提升能力相应增加的同时，提升机的振幅也成比例增加，但并不影响提升机的正常工作，对高空作业环境影响不大。

传动提升机机身温度变化可以反映摩擦传动中相对摩擦量的多少，而在钢丝绳提升机构中主要的摩擦热来源于钢丝绳与绳轮间的摩擦，从表4-2中的数据充分验证了这一点。由于S形提升机的散热面积较大，在其优越的提升能力下，运行过程中机身温度并不是最高的，在连续工作2h后，机身温度为127.8℃。在α形提升机中，随着绳轮直径的增加，提升机机身温度随运行时间累积上升速度一直趋于平稳，多数提升机在测试100min之后出现连续不变的温度值，可以认为是热量的产生和扩散趋于平衡。绳轮直径为23cm的提升机出现的最高机身温度为130℃，在设计范围内。根据表4-2测试的数据绘制了提升机机身温度变化曲线，如图4-41所示。

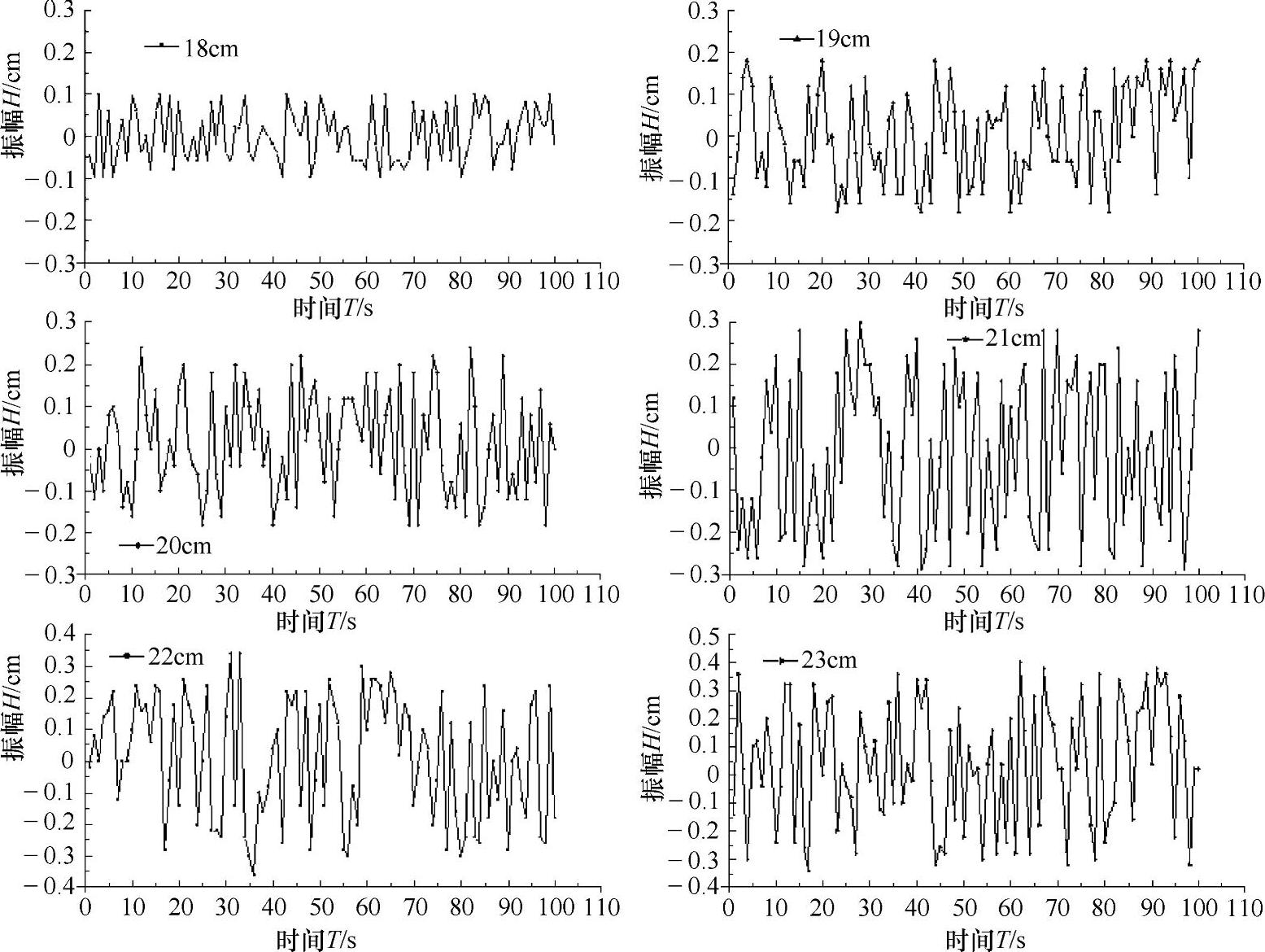
图4-40 α形提升机采用不同绳轮直径的振动曲线

表4-2 测试提升过程温度数据（提升力F=1.0×10³kN往复测试）

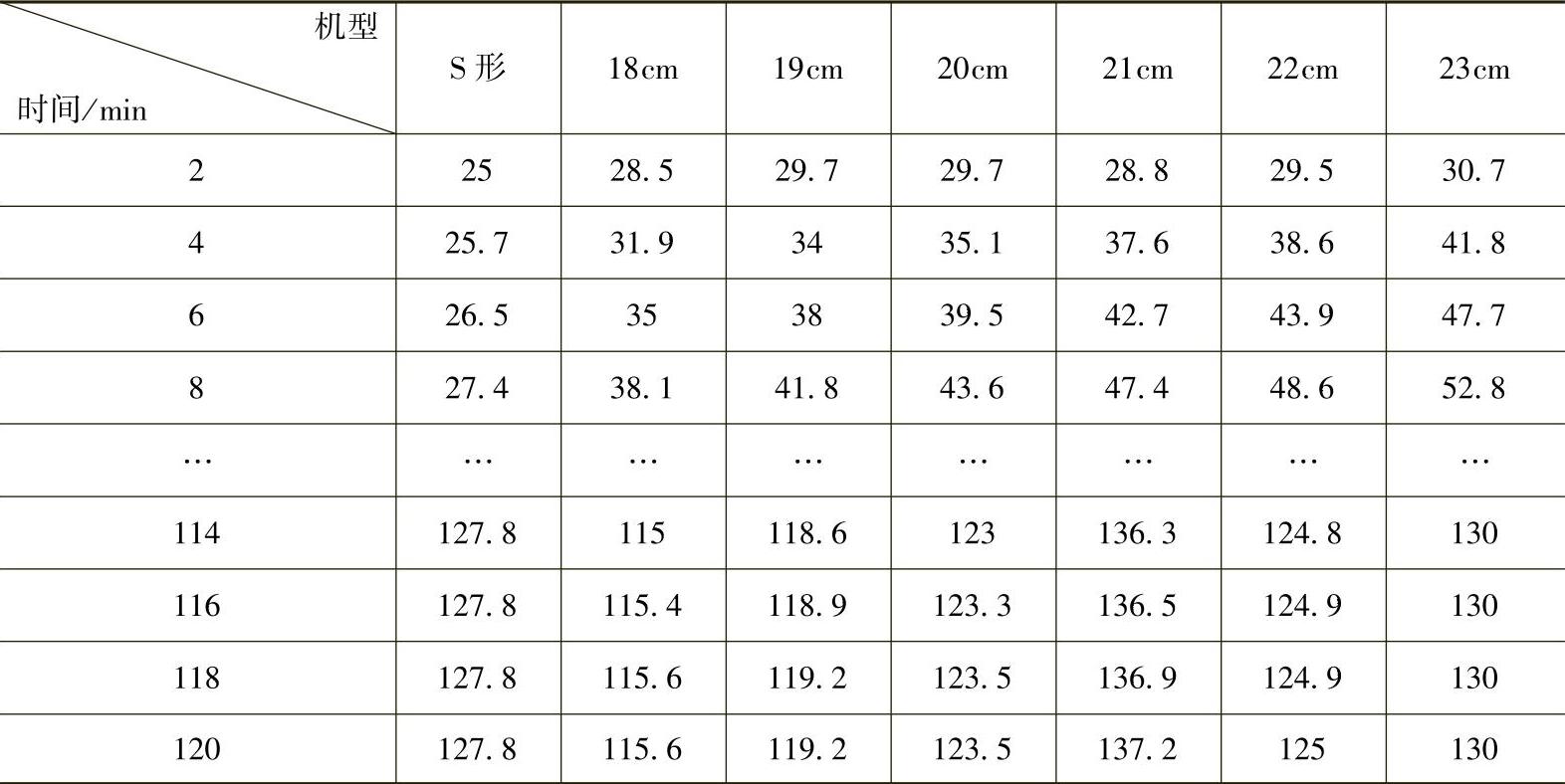
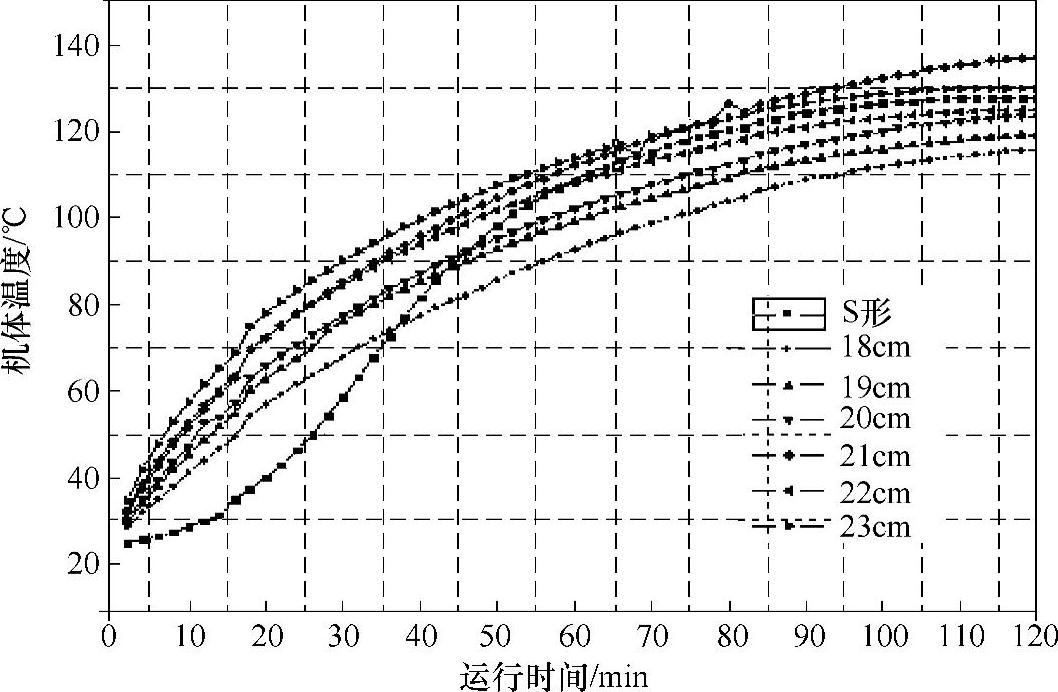
图4-41 提升机机身温度变化曲线

5.绳槽截面形状对提升性能的影响

绳槽与钢丝绳直接形成接触面，其具体形式直接影响到摩擦传动接触面积，及接触间的压力等。根据理论分析，研究中对三种不同结构的绳槽进行试验测试，试验条件为：采用经过测试后的4∗31SW+PP（8.6）镀锌钢丝绳，压绳机构压力为225N，压盘的压强为0.16MPa，绳轮采用40Cr材料加工，测试绳轮直径均设为20cm。图4-42所示为提升机构中三种不同形式的绳槽截面图。

图4-42 三种不同形式的绳槽截面

从图4-42中可以看出：图4-42a所示截面为倒梯形结构，由于钢丝绳为螺旋圆形截面，因此钢丝绳与绳槽形成的摩擦面主要为梯形两腰内表面，最为理想的设计是在最大设计拉力作用下，钢丝绳在包角范围内大部分可以接触到绳槽底面形成摩擦力作用。但由于钢丝绳所受拉力随绳轮的包角变化，这样的优化设计在处理过程中较为复杂。倒梯形截面的设计尺寸为4cm×17cm×8cm，分别是底边宽度、槽深及槽顶宽度；图4-42b所示截面为半圆形槽底，绳槽的主要摩擦接触面积为圆弧形底面，底弧半径为4.15cm；图4-42c所示采用两片夹板形成绳槽，通过弹簧作用进行压紧，绳槽截面为矩形，槽底宽度为5cm。

试验过程对配备不同绳轮绳槽结构的提升机构在不同提升力下进行滑移量测试，记录提升机构自身振动及运行中机身温度的变化，得出相应的测试数据。

图4-43所示为不同绳槽截面提升机整机提升性能曲线。

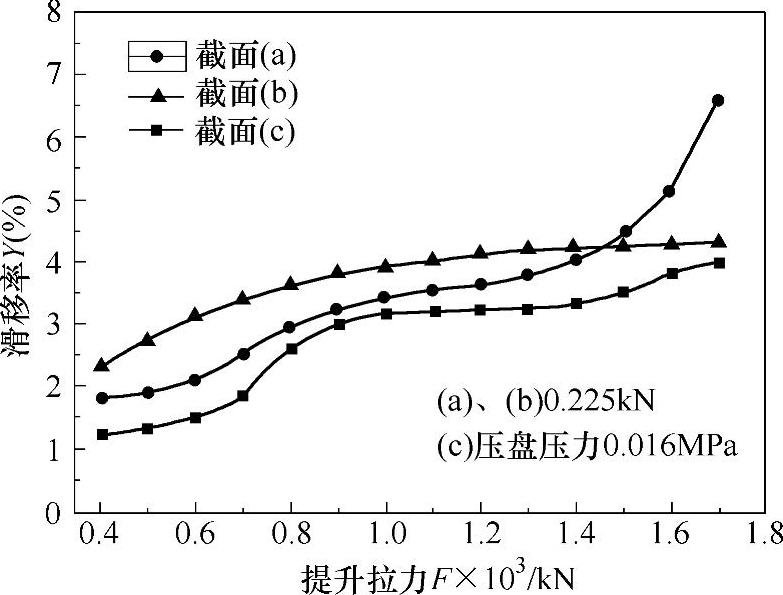
图4-43 不同绳槽截面提升机整机提升性能曲线

从图中可以看出性能最好、滑移量最小的是采用两片夹板形成绳槽截面（c）提升机；倒梯形结构截面（a）提升机在小拉力作用下表现优良；半圆形槽底截面（b）提升机性能稳定，滑移率几乎不受拉力作用影响。数据表明α形压绳机构在压力为225N、压绳盘压力为0.016MPa的条件下，三种形式的提升机整体性能均表现优良，最大滑移率出现在提升拉力为1.7×10³kN的倒梯形结构截面（a）提升机，其值为6.67%；半圆形槽底截面（b）提升机在较大拉力作用下性能表现较好，适合开发大提升力的提升机构，有待进一步深入研究。

在钢丝绳提升拉力处于1.0×10³kN的条件下测试振幅（图4-44），测得数据表明压盘式提升机构比压绳机构振幅范围大，与上面试验得到的数据相符。（a）截面提升机构与（b）截面提升机构相比，后者的振幅相对较大，这一规律的成因还不明确。同时，在试验中发现振幅与钢丝绳磨损程度间存在相应的内部关系，振幅较大的钢丝绳在相同工作时间内磨损程度较大。

从获得的温度测试结果（图4-45）中发现，截面为（a）的提升机在2h的测试中波动较大，其他两个截面的提升机相对平稳，运行过程中的机身温度与提升机在提升过程中的振动存在相互的对应关系。

6.压绳机构对提升性能的影响

压绳机构同样是与钢丝绳直接接触形成接触面的结构，其具体形式直接影响到摩擦传动效率。同时，压绳机构提供给钢丝绳的压力，将直接影响钢丝绳的运行寿命。从上面的测试结构中可以得到这样的结论：绳轮盘压绳结构可以改善钢丝绳的提升能力。摩擦绳轮在压缩和剪切模式下的黏弹性力学性能并非定值，而是随提升拉力和加载时间而变化，两种提升结构的复合模量值比较接近。压绳机构的压力值随弹簧数目的增加而非线性增大。如图4-46所示，当采用盘式压绳结构时，绳轮绳槽压缩储能模量值最大，而采用压绳机构时，则增加的是钢丝绳离开端的出绳压力，且两者在作用后差值随提升拉力的增加而逐渐缩小，最小差值接近于零。

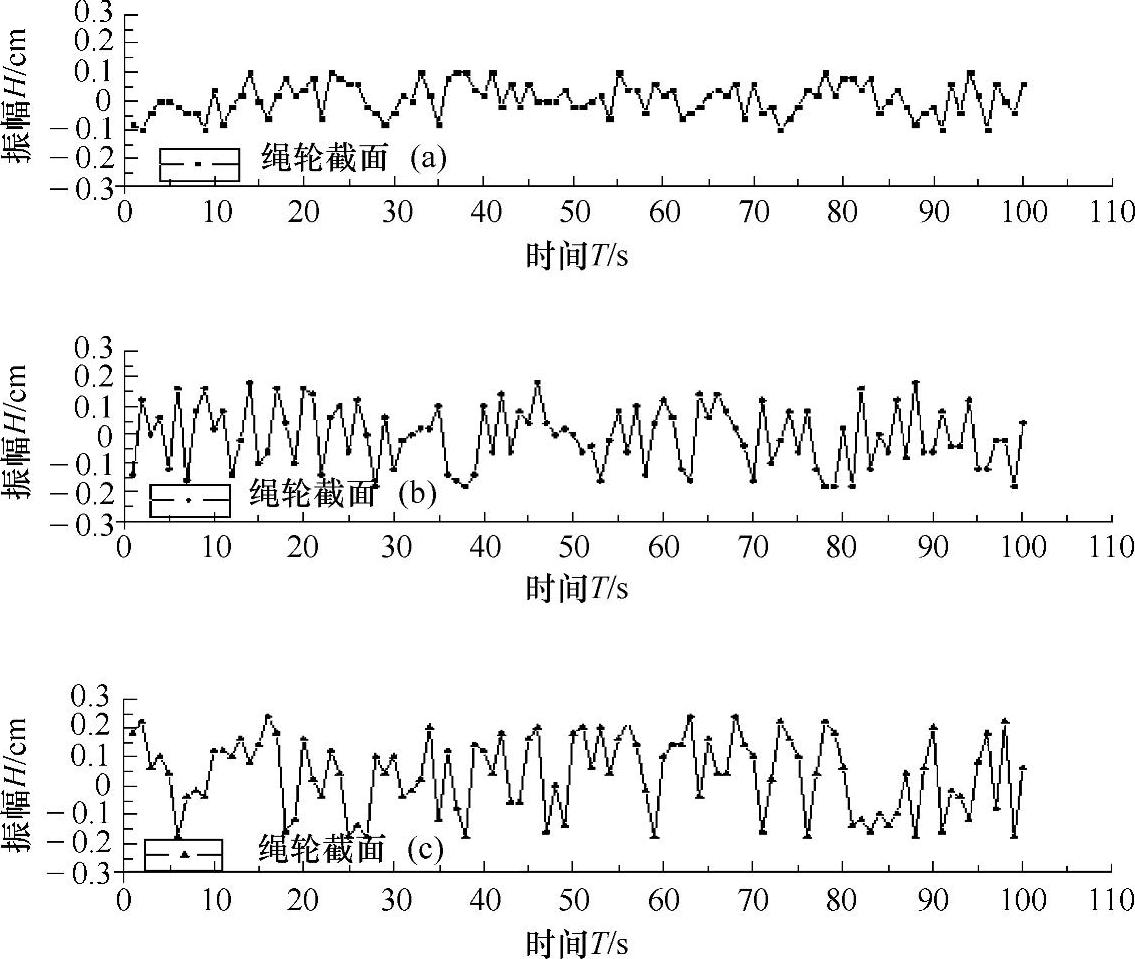
图4-44 钢丝绳提升能力过程中的振动曲线

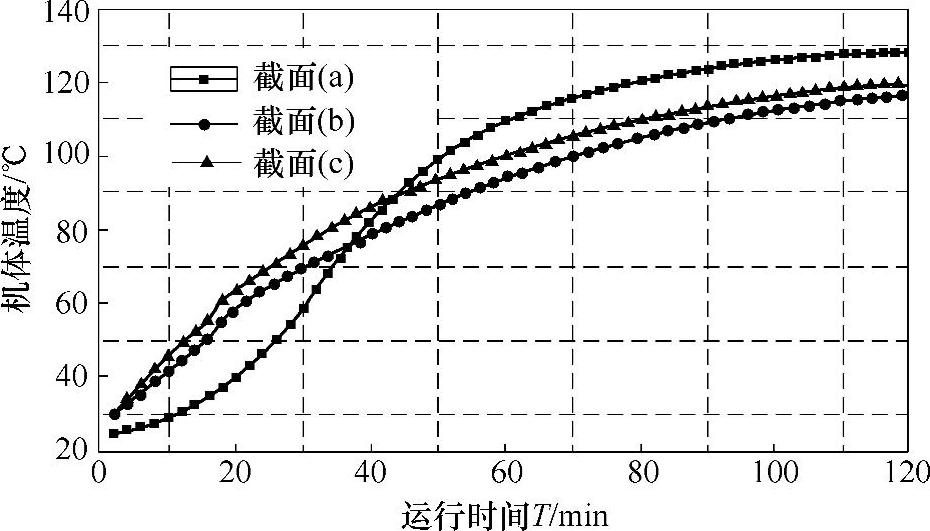
图4-45 提升机能力测试过程中的温升曲线

图4-46 三种压绳机构形式

在测试中采用镀锌钢丝绳，压绳机构的压力按标准设定为225N，压盘式压强为0.016MPa，摩擦绳轮的材料为40Cr。试验过程对配备不同压绳机构的提升机构进行提升力性能测试，同时检测了提升过程的振幅变化及机身温度变化，得到测试数据并绘制相应的测试曲线（图4-47），反映了压绳机构对提升机构提升能力的影响。

图4-47中b）c）两种压绳机构在提升滑移率上区别不大，盘式压绳机构在提升拉力较小时，摩擦拉力性能较好，在提升拉力逐渐增大时，其滑移率的上升趋势增大，在提升拉力为1.6×10³kN时，两种压绳机构对应的数值几乎相同。

振幅如图4-48所示，三者振幅差别不大，遵循之前的规律，盘式压绳机构的振幅大于另外两种形式，压绳机构（c）在结构上得到优化，其振幅相对压绳机构（b）有所改善。

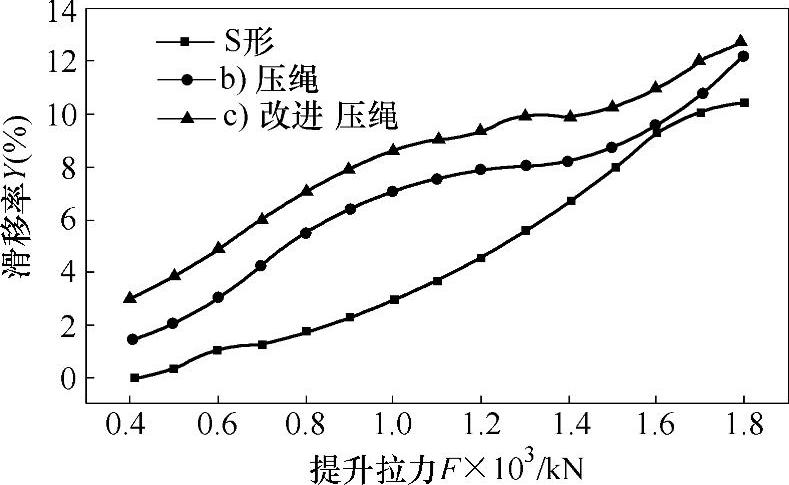
图4-47 压绳机构影响提升能力曲线

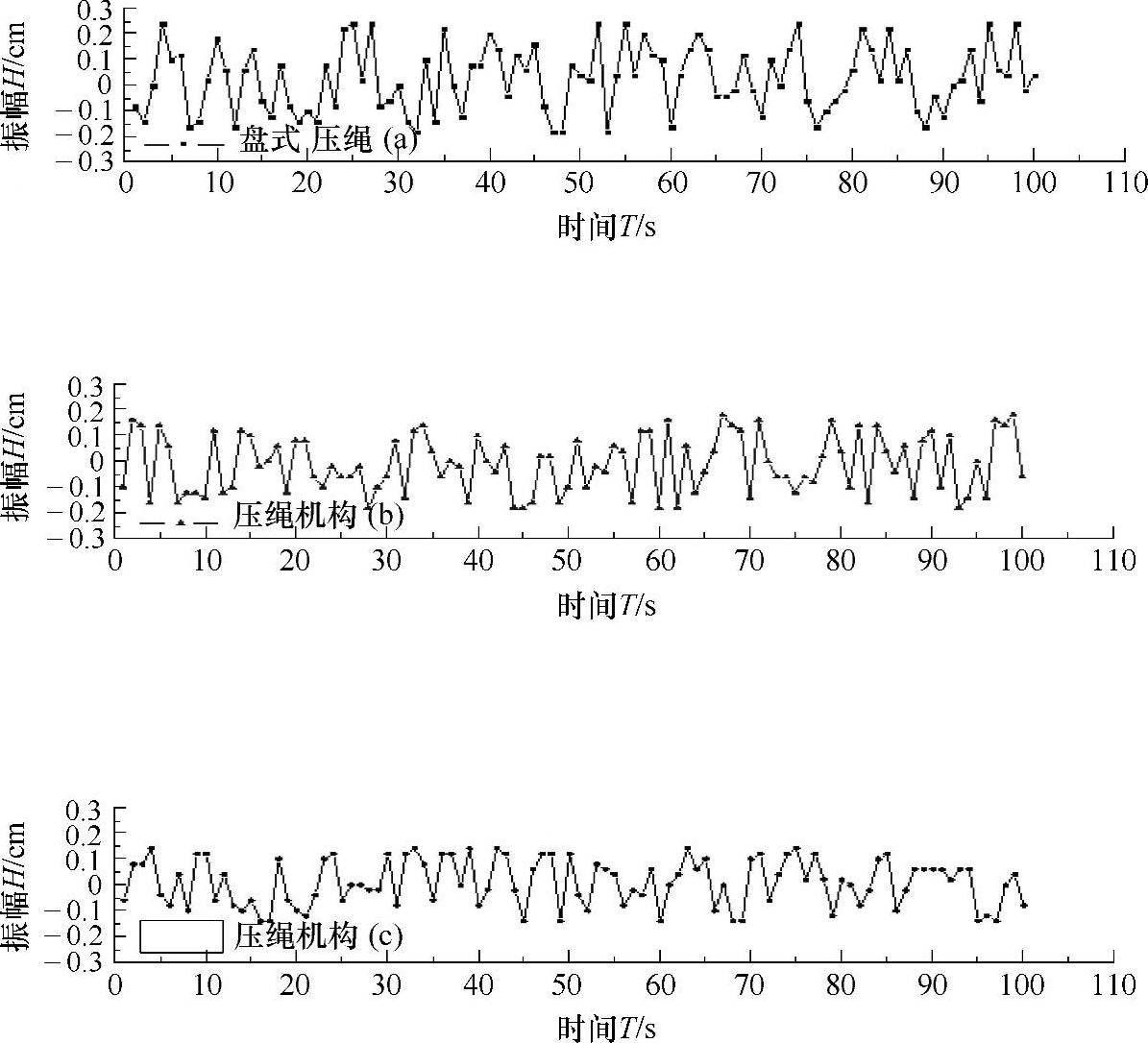
图4-48 压绳机构影响提升能力测试中的振幅

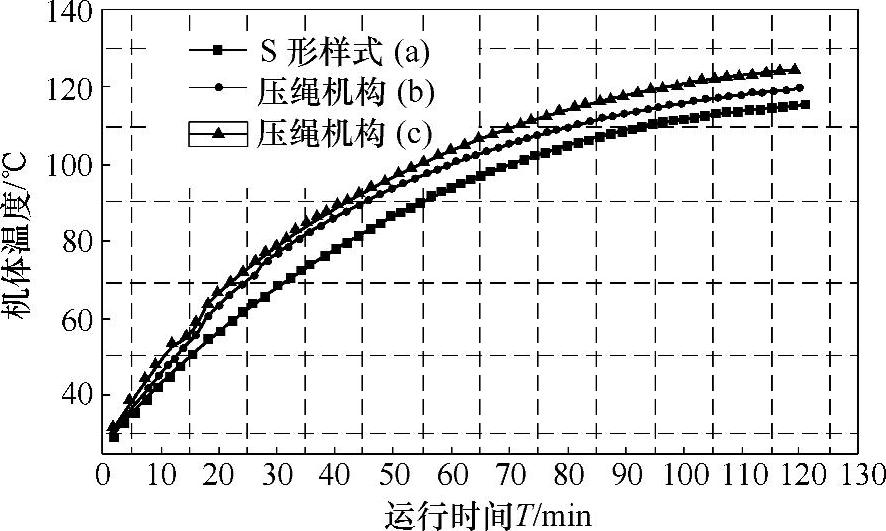
图4-49 压绳机构影响提升力测试中的温升曲线

从温升曲线（图4-49）可以得到，机身温度升高最慢的为S形结构的盘式压绳机构，这主要是该提升机的体积较大，散热面积相对较好。而改进后的压绳机构由于优化了压绳作用面、压绳片形状及比例位置，增大钢丝绳与绳轮间的相互摩擦作用力，提高了提升作业效率，导致机身温度整体略高于改变前的提升机构。