摩擦传动中按照柔性体传动的蠕变理论，钢丝绳与绳轮的接触过程存在不产生滑动摩擦力的静接触区、产生滑动摩擦力的滑动区、静接触区与滑动区之间的过渡区。如图4-27所示为钢丝绳摩擦传动分区作用划分。

图4-28给出了提升机构摩擦传动形式中柔性体与刚体接触摩擦因数的变化趋势。

由于摩擦传动过程中钢丝绳自身的弹性差异，拉力差的变化和运行速度改变等因素的影响，不同规格的摩擦传动机构，钢丝绳的滑动速度是不同的。经推导可以得到滑动速度的计算公式为

式中 ΔT——摩擦轮两侧钢丝绳拉力差（N）；

v₀——摩擦传动中钢丝绳的线速度（mm/s）；

E——钢丝绳的拉伸弹性模量（MPa）；

A——钢丝绳当量横截面积（mm²）。

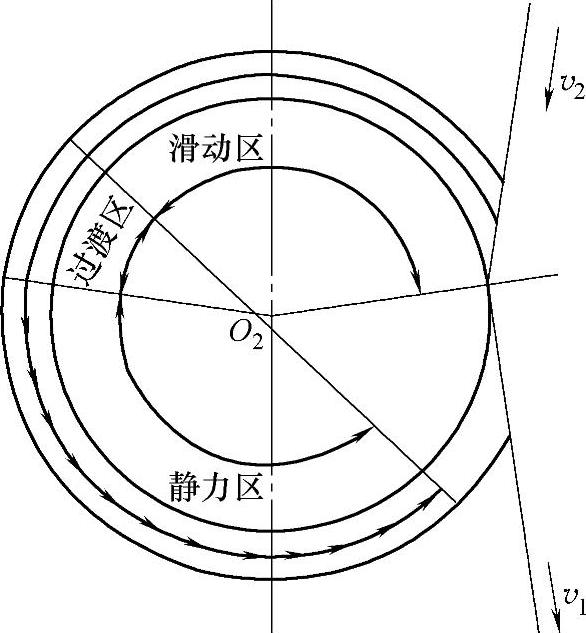
图4-27 钢丝绳摩擦传动分区作用划分

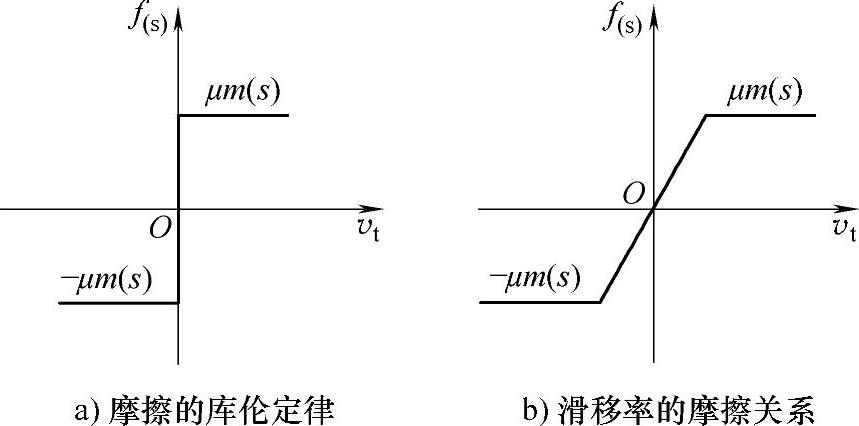
图4-28 钢丝绳与绳轮摩擦规律

研究表明，钢丝绳的滑动（蠕动）速度对摩擦传动性能有很大的影响，单纯从速度影响角度分析，滑动速度增大会使当量摩擦因数适当提高，但同时会增加系统磨损程度。

假设钢丝绳摩擦传动过程中钢丝绳长度发生变化量为ε（α），微元上钢丝绳拉力较小端的拉力为F_wi，获得的摩擦力为F_m，由拉力引起对绳轮的正压力为F_Q，钢丝绳微元对应圆心角为2θ=α，对应的弧长为2θr，r为绳轮中心到钢丝绳中心的半径，钢丝绳与绳轮间的修正摩擦因数为_μx，k钢丝绳的刚度系数，钢丝绳弹性模量E_r。研究提升机构摩擦传动过程，采用质量守恒定律给出下面公式

G=ρ（s）v（s）A（s）=ρ_iv_iA_i （4-51）

式中 ρ（s）、A（s）——钢丝绳的密度和计算截面积；

v（s）——钢丝绳传动的速度；

i——摩擦传动过程中对应的时刻。

由钢丝绳微元能量守恒可以得出相应公式

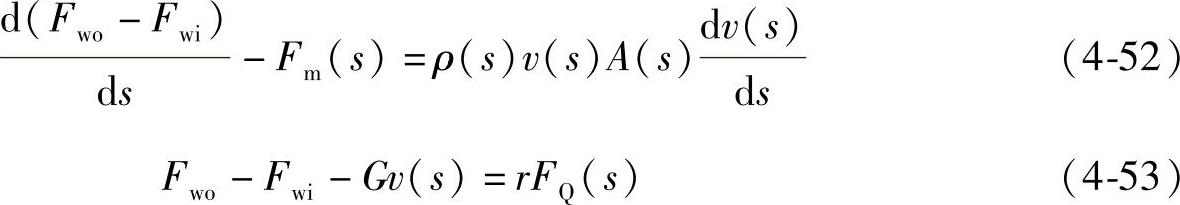
结合钢丝绳摩擦传动修正后的摩擦力计算公式

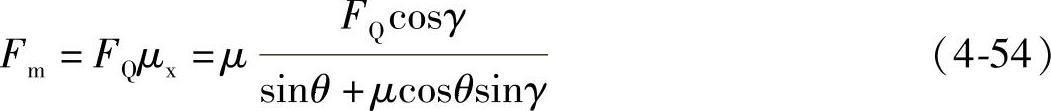
根据式（4-36）推导的钢丝绳弹性变形量计算公式可得(www.daowen.com)

F_wo-F_wi=E_rε（s） （4-55）

式中 E_r=E_c′cos⁴ω₁cos⁴ω₂。

钢丝绳与绳轮接触过程中钢丝绳速度变化量为

v（s）=v_i（1+ε（s）） （4-56）

钢丝绳摩擦传动中，在动力优先的摩擦传动形式下，其钢丝绳的动量守恒方程如下

F_wo+F_wi=G（v_wo+v_wi） （4-57）

（F_wo-F_wi）r+Gr（v_wo+v_wi）=M （4-58）

式中 v_wo、v_wi——钢丝绳进入端和离开端速度分量，v_wo=v_i（1+F_wo/k），v_wi=v_i（1+F_wi/k）。从钢丝绳变形的换算关系可以得到

ds/（1+ε（s））=ds₀ （4-59）

联立式（4-57）、（4-58）、（4-59）可得到滑动区域钢丝绳拉力的计算公式

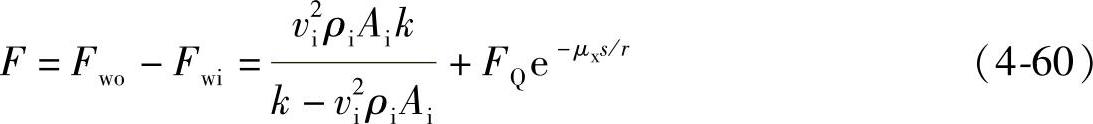
式中 F_wi——滑动区钢丝绳进入端拉力；

F_wo——滑动区钢丝绳离开端拉力；

F_Q——钢丝绳对绳轮的正压力；

r——绳轮中心到钢丝绳中心的半径；

μ_x——钢丝绳与绳轮间的修正摩擦因数；

k——钢丝绳的刚度系数；

i——摩擦传动过程中对应的时刻。

摩擦传动中相对滑动角区域的确定，从实际理论可知钢丝绳摩擦传动的弹性滑动总是发生在钢丝绳摩擦传动力较大的一侧，如图4-29所示钢丝绳绳轮上的弹性滑动角出现在AB段，这点可从理论上给予说明^[39] 。

在图中摩擦绳轮上采用净截面积为A的钢丝绳进行工作，紧边受拉力较大，钢丝绳截面积将相应变小，截面积的变小，使钢丝绳承受的作用力变大，因此容易出现滑动。而松边受拉力相对较小，绳的截面积接近常态钢丝绳的净截面积A，设计过程中绳轮与钢丝绳存在一定的过量关系，因此在这段出现滑移的可能性较小。

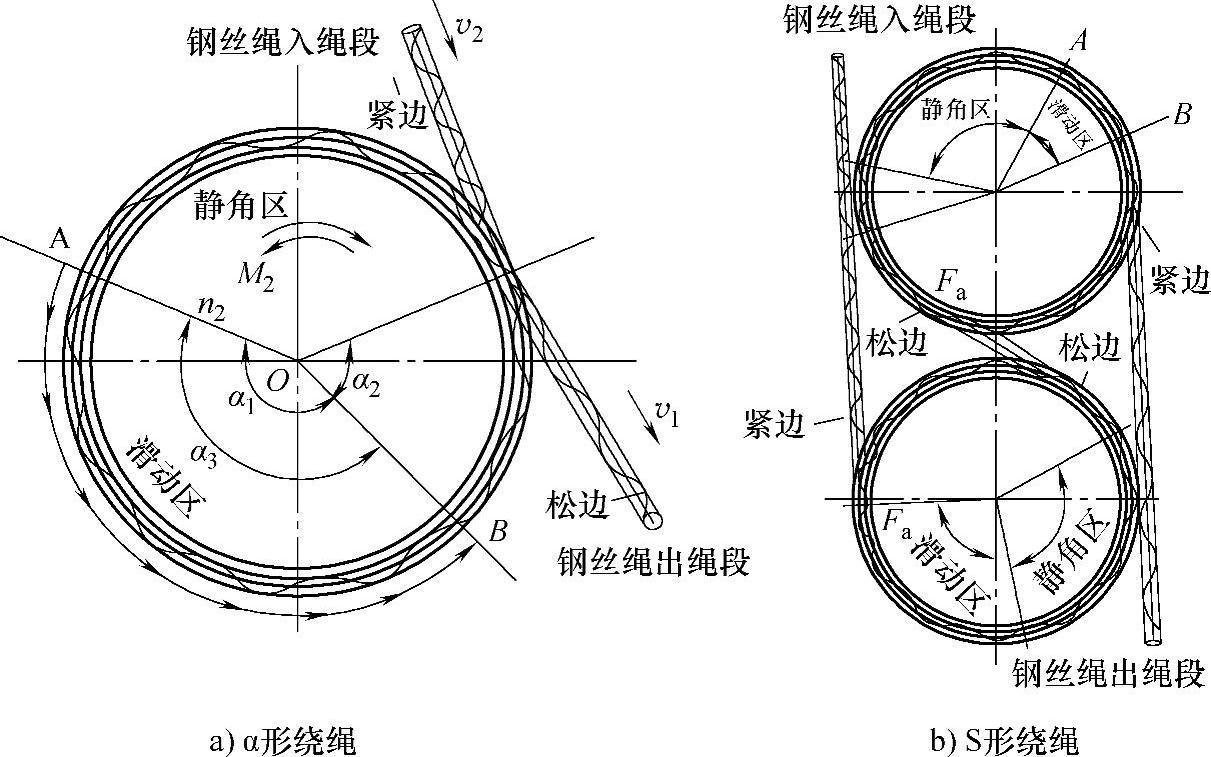
图4-29 钢丝绳摩擦传动的滑动区