摩擦传动提升系统通过传动摩擦轮与柔性钢丝绳之间的摩擦产生提升力^[33] 。在动力传递过程中，柔性钢丝绳通过其表面的摩擦力拉动负载，即钢丝绳与绳轮构成摩擦副，实现动力传递。摩擦轮与钢丝绳传递力的大小主要与钢丝绳在绳轮上的包角有关，为了增加包角，研究人员给出了提升机构摩擦传动的两种不同绕绳方式，如图4-21所示。

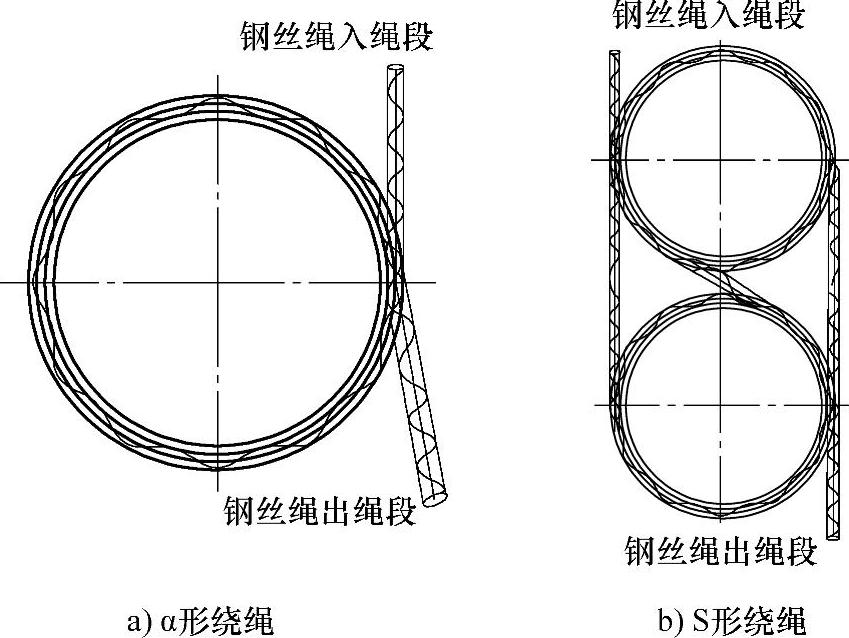
图4-21 柔性钢丝绳摩擦传动绕绳示意图^[34]

图4-18a所示为α形绕绳，该绕绳方式结构复杂，动力传递性好，适合重力不大的负载提升过程，整个绕绳过程不改变钢丝绳的接触方向，有效延长了钢丝绳的寿命。图4-18b所示为S形绕绳，该方式大大提高了钢丝绳在绳轮表面的包角，绕绳过程改变了钢丝绳的绕绳面，可以使钢丝绳工作磨损均匀，但在大载荷作用力下对钢丝绳的破坏较为严重。

钢丝绳是弹性体，其摩擦传动主要依靠钢丝绳与绳轮间摩擦力实现。因此要保证正常运行，需要通过改变摩擦结构及设计相应压绳机构来有效地提高摩擦因数，减少摩擦滑动量，进而提高提升系统的提升性能。对摩擦传动进行建模，研究各参数对摩擦传动力的影响。

对计算模型中的钢丝绳提出必要的简化条件，其中包括认为钢丝绳在摩擦传动段不存在弹性变形及钢丝直径的差异，且在绳轮圆周包角处摩擦状态可认为是恒定不变的。所以，随着钢丝绳提升载荷的不断增大，当其达到绳轮与钢丝绳间摩擦力的稳定传递极限时，钢丝绳将进入打滑传递阶段，钢丝绳与绳轮间作用力如图4-22所示。

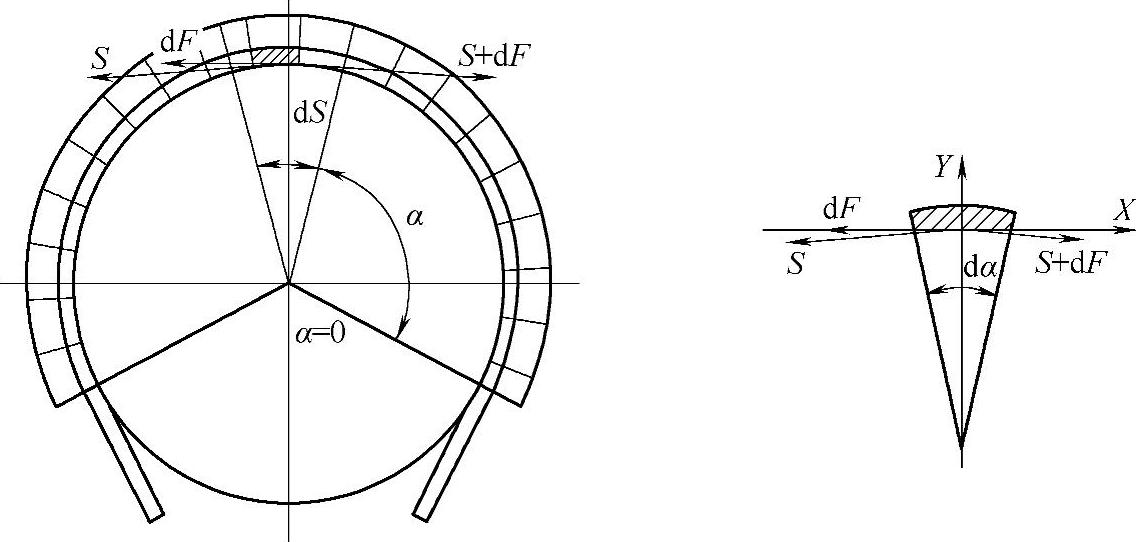
图4-22 钢丝绳与绳轮间作用力^[35]

针对钢丝绳微元dS进行受力分析，给出坐标轴方向体力平衡方程如下

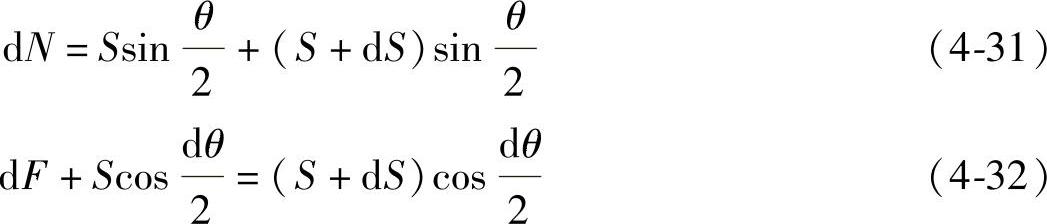
dF=μdN （4-33）

式中 θ——钢丝绳在一段绳轮上的包角；

S——钢丝绳在绳轮上的接触总长度；

dN——钢丝绳所受的法向作用力；

μ——钢丝绳与绳轮间的摩擦因数，可以通过推导公式进行计算。

其微元摩擦作用接触包角dθ变化较小，可近似表示，。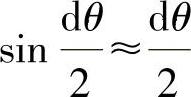

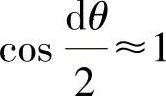对式（4-34）两边进行积分，可以得到

将边界条件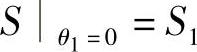代入，得出S=S₁·e^μθ为绳轮包角任意位置张力S的推导公式，该式为摩擦传动的Euler公式。将边界条件|S_θ=α=S_ymax代入推导公式中，可以获得张力S的最大值为S_ymax=S₁·e^μα，为极限摩擦状态下绳轮与钢丝绳所形成的最大张力，其中e为自然对数函数的底数。

根据推导得到的公式，可知系统中各参数间的关系，为了提高摩擦传动的提升能力，可以通过三个方面考虑：

（1）增加初始预紧力 增加初始预紧力可使钢丝绳在传动摩擦轮分离位置的作用力增大。摩擦传动中由于钢丝绳的长度会有一定变化，初始拉力因钢丝绳增长而降低，造成摩擦传动能力减弱，工程实际中常通过提高初始预紧力以提高提升性能。

（2）选择较大摩擦因数的接触材料 通过选择合适的材料增大钢丝绳与摩擦绳轮之间的摩擦因数。采用与柔性钢丝绳间存在较大摩擦因数的材料制作绳轮，提高摩擦接触系数。用这种方法可以不用增加钢丝绳的张力，而提升摩擦传动提升机构的提升力。

（3）改变钢丝绳摩擦接触角 摩擦接触角是决定钢丝绳摩擦传动提升力的主要参数，采用S形绕绳方式可以提高接触范围，较好地改善钢丝绳摩擦传动的提升能力，但可能对钢丝绳产生破坏。

上述三种改善钢丝摩擦传动的方法，其中工程实际中采用最为有效的方法是前两种，而采用第一种方法可能使钢丝绳的工作拉力过度增加，增加形成断绳的危险因素机率并可能缩短提升机构的寿命。在理论研究中，可以通过优化提升机构设计有效地提高提升能力。

1.钢丝绳摩擦传动力学分析

钢丝绳在工程应用中可作为弹性体进行研究，在摩擦传动过程中，钢丝绳与绳轮间形成摩擦力使主动绳轮带动钢丝绳完成传动，钢丝绳进入绳轮端和离开绳轮端受到不同的拉力作用，形成不同的拉伸弹性变形，使钢丝绳发生类似蚯蚓爬行的蠕动现象，产生弹性滑动。因此钢丝绳传动与带传动相似，这种弹性滑动是摩擦传动中固有的、不可避免的力学现象。但是由于钢丝绳摩擦传动应用形式具有多样性，精密钢丝绳摩擦传动的传动绳两端通常在从动轮上固定，矿井和建筑提升中的钢丝绳一端固定，另一端采用重物保证钢丝绳张紧力，防止钢丝绳与绳轮间产生相对滑动。此类摩擦传动的设计主要对绳轮驱动力进行研究，优化了提升性能避免出现打滑失效。常用传动欧拉公式对摩擦传动特性及钢丝绳中摩擦绳轮的压力和摩擦作用力进行研究。

传动的钢丝绳进入驱动绳轮端拉力F_i与离开绳轮端拉力F_o间的关系用弹性体摩擦欧拉公式（图4-23）表示为

F_o=e^μθF_i （4-36）

式中 _μ——钢丝绳与绳轮间的摩擦因数，由于钢丝绳自身结构特殊性，在采用欧拉公式进行计算时，需要对摩擦因数进行修正处理得到钢丝绳摩擦传动更为准确的表达式；

θ——钢丝绳与绳轮间的包角。

摩擦绳轮除受到钢丝绳的摩擦作用力及自身重力外，还受到传动轴输入的扭矩作用。输入扭矩引起钢丝绳在绳轮表面的作用力变化，可以通过作用在绳轮法向的正压力P和沿圆周的切向摩擦力f表示其变化。钢丝绳对绳轮的压力沿绳轮圆周方向是连续变化的，其计算公式为F_o=e^μθF_i，沿圆周的切向摩擦力的值为f=μe^μθF_i，二者均按指数关系沿绳轮包角发生变化，具体绳轮表面的摩擦力分布如图4-24所示。

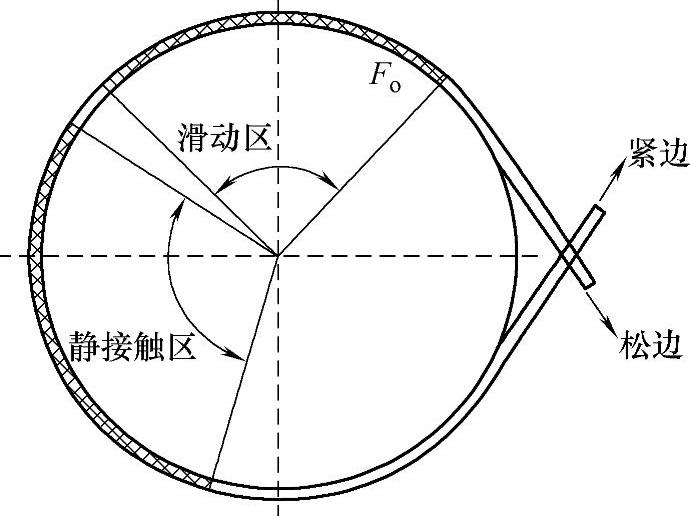
图4-23 钢丝绳摩擦传动的欧拉公式^[36]

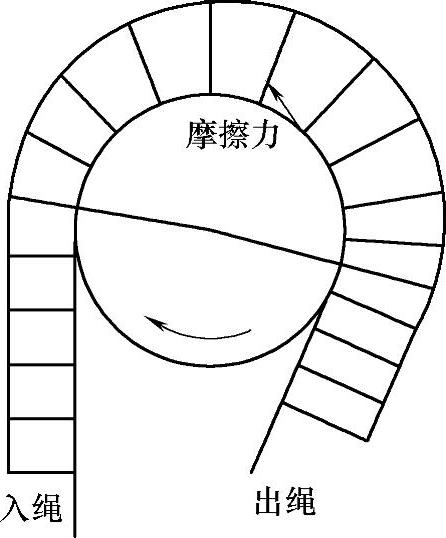
图4-24 绳轮表面的摩擦力分布图^[37]

由于绳轮表面的滑动区和静接触区并不明确，所以实际计算中假设在整个绳轮表面沿钢丝绳传递方向内均满足欧拉公式。

2.考虑摩擦绳槽角度效应的弹性滑动量

考虑绳槽结构的不同作用，当钢丝绳摩擦传动绳轮依靠钢丝绳与绳槽底部接触形成摩擦力实现传动时，摩擦因数应该为两种材料间的摩擦因数；而当钢丝绳在楔角为ϕ的楔形绳槽中通过时，其摩擦因数不仅与材料的摩擦因数_μ有关，还受钢丝绳与绳轮间的接触形式影响，在仅考虑楔角的作用时，经过力的分析可以获得钢丝绳传动的修正摩擦因数_μx为

(www.daowen.com)

进一步考虑钢丝绳在绳槽内受到切向滑动作用力，根据受力平衡关系可以将上面修正摩擦因数精确到钢丝绳在绳轮内的总摩擦因数为

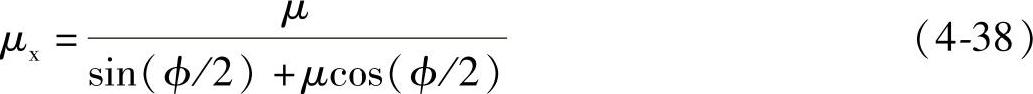
研究中还需要考虑钢丝绳进入和离开绳轮两端的不同作用力对摩擦因数的影响，以及滑动摩擦和静摩擦的摩擦因数变化。

最为理想的接触状态是钢丝绳与绳轮接触面最大化，即钢丝绳与绳轮的两个侧面及底面均有良好的接触状态，在钢丝绳受拉力及弯曲作用时，其自身结构、形状均发生较大变化。从钢丝绳进入到离开绳轮的整个过程中，摩擦传动形式不同，钢丝绳的受力形式相似。图4-25所示为目前常用的钢丝绳绳轮的截面形式。

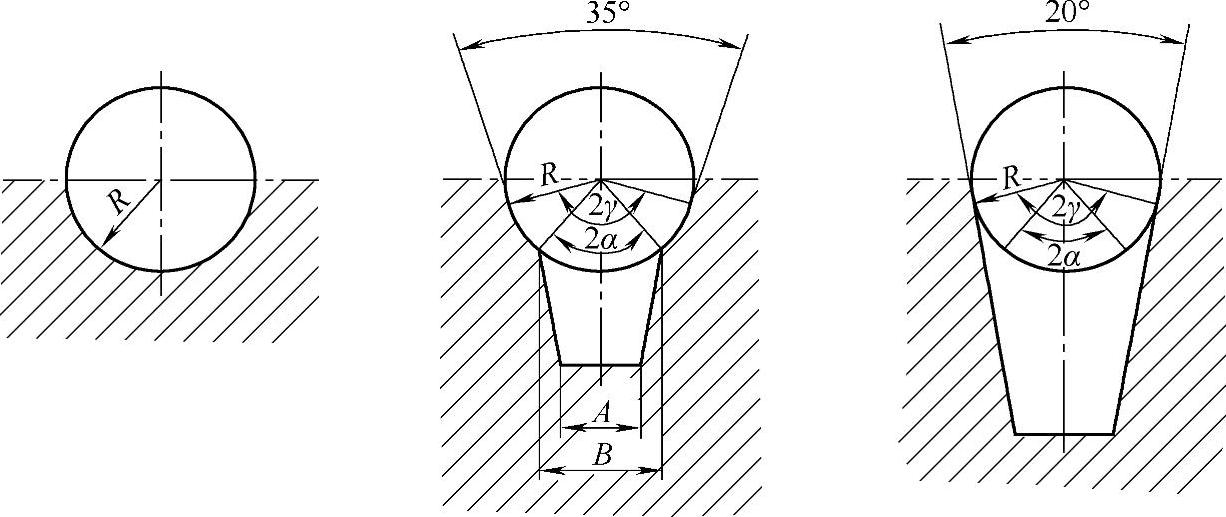
图4-25 常用的钢丝绳绳轮的截面形式^[38]

在钢丝绳摩擦传动的研究中，主要的控制参数之一为γ角，其为钢丝绳提供摩擦作用的主要计算变量。该角表示钢丝绳传动时，钢丝绳沿轮槽径向滑动产生的径向摩擦力F_j，由于径向摩擦力的作用使周向摩擦力F_z与钢丝绳作用拉力F_l形成的夹角。摩擦钢丝绳进入到离开绳轮的过程中，钢丝绳的摩擦力状态可以分为三个子过程进行描述：

1）钢丝绳绕入端，钢丝绳作用力相对绕出端要大得多，钢丝绳在绳轮间径向上会产生指向绳轮的径向作用力，进而形成径向摩擦力F_j、周向摩擦力F_z与钢丝绳作用拉力F_l，F_l与F_z形成夹角γ。

2）钢丝绳在进入绳轮适当的位置，由于钢丝绳受到的拉力适中，使钢丝绳运动轨迹符合设计轨迹，钢丝绳没有沿径向滑向绳轮内部，因此产生的径向摩擦力F_j的方向垂直于钢丝绳作用拉力F_l，钢丝绳作用拉力F_l与周向摩擦力F_z重合形成的γ角为零。

3）钢丝绳绕出绳轮部分，由于钢丝绳受到的拉力减小，使得钢丝绳向绳轮内部的径向滑动量变小，使钢丝绳作用拉力F_l与周向摩擦力F_z形成相反方向的夹角-γ。

从划分的不同阶段来看，在各部分形成的角度大小和方向各有不同，所以在分析钢丝绳摩擦因数的计算方法时应该将角度γ考虑在内。

通过分析一小段钢丝绳微元的受力情况，得到其沿钢丝绳在周向上力的平衡方程如下，其中将微元两端受力分别定义为F_wi、F_wo，微元对应的包角为2θ，r为蜗轮中心到钢丝绳中心的半径

F_wicosθ+4F_zrθ-F_wocosθ=0 （4-39）

沿径向受力分析为

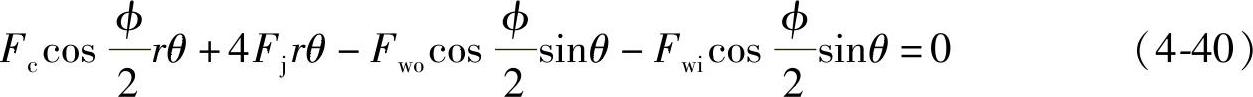
采用数学简化方法，将公式取极限得到简化式为

4F_zrθ-（F_wo-F_wi）cosθ=0 （4-41）

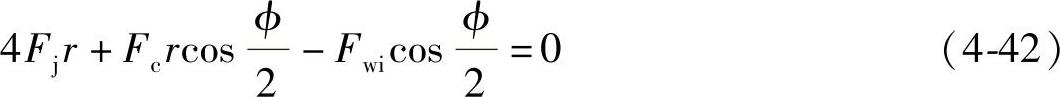
进一步得到微分形式

几何关系影响角的正切值为微元径向摩擦力F_j与周向摩擦力F_z之比，代入公式得到

联立下面关系式

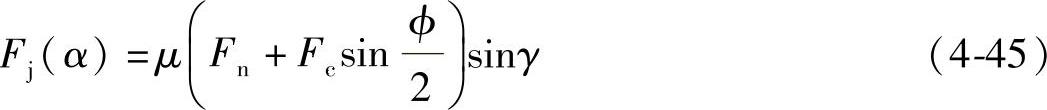
式中 F_n——钢丝绳外层绳股的作用力；

F_c——钢丝绳中心绳股的作用力。

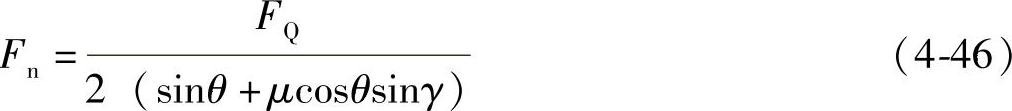
式中 F_Q——钢丝绳对绳轮的正压力（N）；

θ——微元对应的圆心角（°）。

钢丝绳摩擦传动稳定状态下，钢丝绳横截面及其垂直面受力应满足力的平衡关系，联立径向摩擦力F_j=μF_Qxsinγ与周向摩擦力F_z=μF_Qxcosγ，从而得到

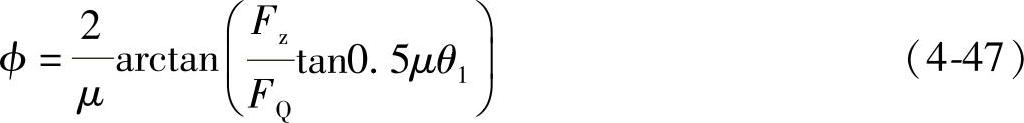
这就使我们得到的一个新的公式，即绳轮上任意位置的力矩与最大力矩之间的比值，等于对应时刻钢丝绳弹性滑动角度的双曲线正切值与包角的算数曲线正切值之比，即

式中 A₁——钢丝绳总的截面积；

A₂——钢丝绳绳心的有效截面积。

分别假定钢丝绳摩擦因数μ为0.3，0.35，0.4，…，0.5；假定F_z/F_Q分别为0.1，0.23，…，1.0；将包角参数θ设定为320°（α形绕绳方式），对应摩擦绳槽的修正摩擦因数_μ′=μsin（ϕ/2），计算得到对应的弹性滑动量为ϕ_h。采用式（4-49）得到三者间的关系曲线如图4-26所示。

图4-25中给出了不同摩擦因数下弹性滑动量的变化规律，当绳轮上任意位置的力矩与最大力矩之间的比值及包角一定时，不同摩擦因数对应不同的弹性滑动曲线。从图4-25可以看出，随绳轮包角位置的增加，绳轮上任意位置的力矩与最大力矩之间的比值从0增至1，此过程中钢丝绳在绳轮表面弹性滑动量的变化趋势为先慢后快。

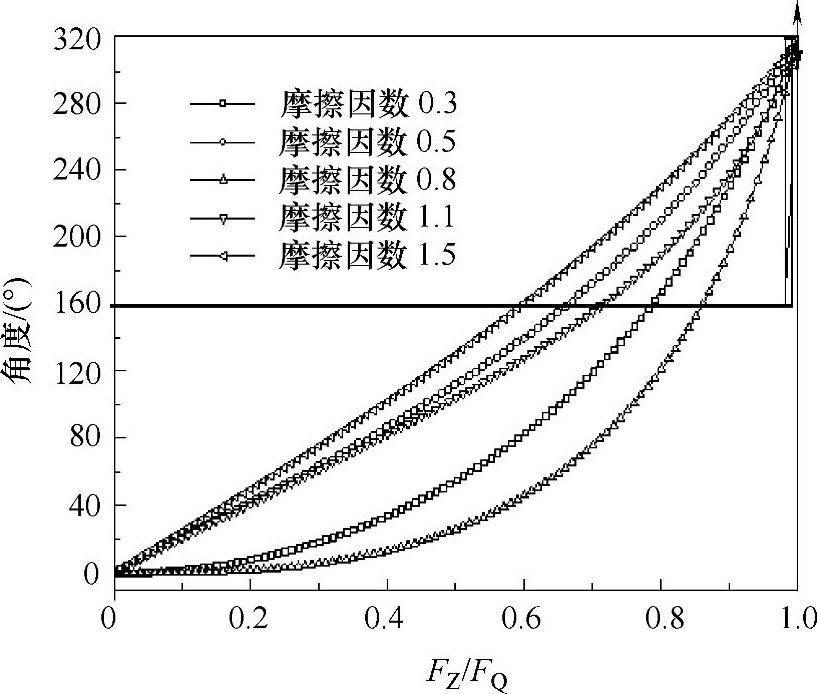
图4-26 弹性滑动量变化规律