总结研究人员的研究成果发现，在用柔性钢丝绳绳股力学特性分析模型解决常规载荷作用下的力学问题时，对钢丝绳绳丝间的切向接触和摩擦效应未进行深入研究，从而使其研究结果只能适用于润滑很好的钢丝绳，这不符合实际工程情况。从技术方面考虑，对钢丝绳传动，特别是钢丝绳参与主、从动绳轮的复合摩擦传动方面的研究薄弱，对柔性钢丝绳摩擦传动机理的研究在我国也正处于发展阶段。在这样的背景下，对钢丝绳复合传动所产生的摩擦作用力进行系统研究是十分重要的。下面将通过几何数学理论完善钢丝绳的数学模型，研究钢丝在多螺旋结构下螺旋角、各层钢丝直径之间的内在联系，基于接触力学理论建立钢丝绳接触力学模型；进一步研究不同载荷下，钢丝绳与绳轮之间的摩擦系数变化关系以及载荷的变化对钢丝绳绳丝磨损程度的影响。

1.轴向拉伸作用下的受力分析

钢丝绳是通过钢丝捻制工艺制造的，钢丝及绳股在钢丝绳内部均以螺旋结构存在，螺旋结构在轴向受力情况下必然会伸长。这样的伸长量由两部分组成，其一为钢丝或绳股的弹性变形，其二为捻制钢丝绳时钢丝或绳股间存在的缝隙，此缝隙受力后形成伸缩变形。前一种变形由材料自身的弹性决定，后一种变形由捻制过程的捻制结构和捻制松紧程度决定。

大量的实践证实，由结构原因引起的伸长量要远远大于钢丝或绳股自身弹性的变形量。

从图4-2中可以找到侧丝与中心丝在一个螺距之间的关系。沿中心丝方向观察螺旋侧丝，侧丝为一个未出现重叠的圆，该圆的半径为中心丝半径r₁加螺旋丝的半径r₂，从而可以得到螺旋角β的正切值为螺距P与该圆周长的比值，具体为

根据弹簧结构型式，钢丝绳钢丝曲率κ和挠率τ的计算公式为

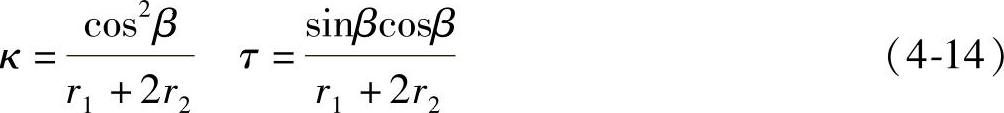
根据单丝未变形和变形的结构，初始状态单丝没有载荷，之后在载荷作用下变形到另一个形状。在受力发生变化的过程中，需要计算钢丝股的扭曲和曲率部分，其计算结果主要取决于钢丝之间的相互接触。沿钢丝中心线移动一个单位速度，方向A、B、C将发生变化。这些方向角度旋转矢量的增加量为ω，这个矢量的预测在A、B和C方向上扭矩的曲率分量分别为κ、κ′、τ（图4-11）、

在给定的截面，有三个力的分量：剪切力N和N′两个部分及扭转力T。还有三对耦合关系：两个组成部分的弯矩惯量G、G′及弯矩H。除了给定的截面力和力矩，还有力的分量，如接触力，以及分布作用在线的外表面上的分布惯量。这些分散的力和力矩分别表示为X、Y、Z和K、K′。

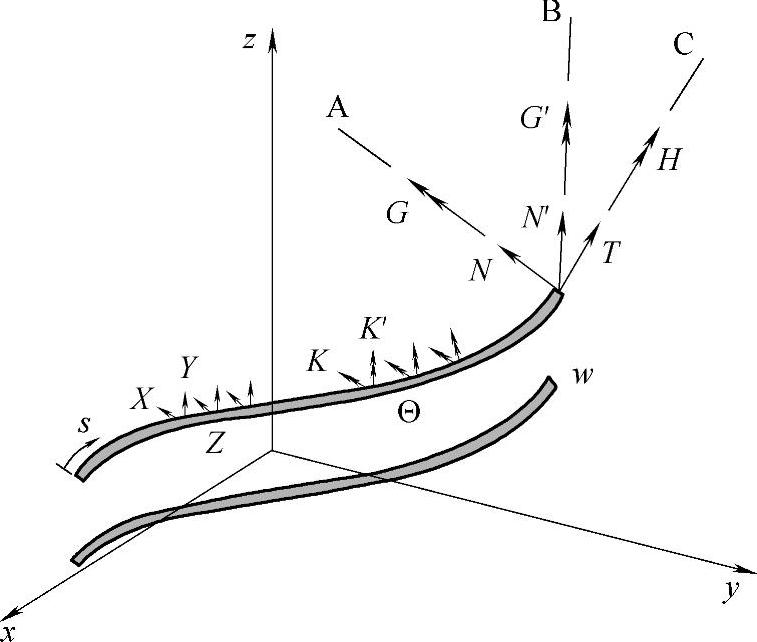
图4-11 钢丝绳中钢丝的变形与受力关系

下面给出钢丝的平衡方程。如果考虑三个方向的力，获得微分方程[28]如下

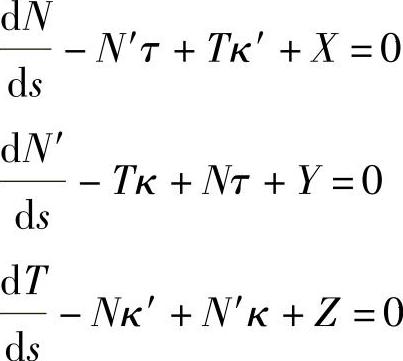
式中 s——沿着钢丝绳轴向的弧长。对动量的三个平衡方程

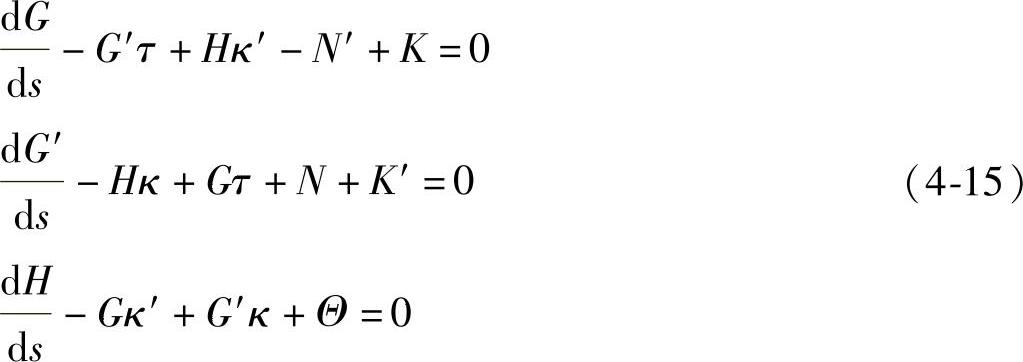
式中 Θ——外界干挠引入函数。

因为存在某些未知的变量，导致得到的方程是非线性的，根据给出的钢丝s可以解上述6个方程。上述的方程大大简化了对螺旋线的描述。除了这些平衡方程外，还需要构建本构关系，即广义力和曲率，扭曲和断裂伸长率分量之间关系[29]

G=EI_x（κ-κ₀）

G′=EI_y（κ′-κ₀′）

（4-16）

H=C（τ-τ₀）

T=EAξ

式中 E——材料的弹性模量；

I_x和I_y——横截面的惯性矩；

C——抗扭刚度；

A——截面积；

ξ——轴向线应变；

κ₀、κ0′、τ0——A、B、C方向上扭矩的曲率分量；

κ、κ′、τ——受力变化前的初始分量。

对于半径为R的圆截面，有

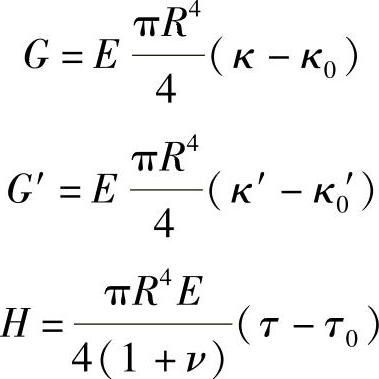
T=EπR²ξ （4-17）

式中 ν——泊松比，表示钢丝绳股的材料特性。

上面所有方程的广义形式也适用于一股钢丝。钢丝绳的弹性模量可以采用苏联的金尼克院士于1931年推导的公式进行近似计算

E_k′=E_ccos⁴ω₁cos⁴ω₂ （4-18）

近似计算的主要理论是通过将钢丝绳中绳丝的螺旋角ω取其平均值为ω₁，将绳股的螺旋角ω取平均值为ω₂，将两个平均值引入单螺旋推导出的钢丝绳弹性模量计算公式中，公式中的E_c为钢丝的弹性模量，进而得到钢丝绳的近似弹性模量E_R′。在随后几十年的研究中，学者们主要是采用修正系数来获取钢丝绳的弹性模量。无法获取钢丝绳弹性模量的原因是钢丝绳由螺旋丝通过捻制成为绳股，绳股经二次或更多次捻制才可制成绳，单纯采用微分几何理论描述螺旋结构进行叠加将使其与实际产生较大偏差。同时，弹性模量这一变量随着钢丝绳投入运行的物理状态的变化而发生相应的变化，大多时候仅可通过实际测试才可以得到特定条件下的特定量。但在研究中，可以通过试验给出钢丝绳弹性模量随不同参数变化的趋势，从而给出规律性变化趋势，揭示定性的变化理论，为钢丝绳模型理论计算提供依据。

考虑钢丝绳弹性模量的另一种方法，认为钢丝拉力与钢丝变形之间存在关系T_s=E_cε_sF，其中ε_s=ε-ε₀，ε₀=γε_r。将其整理推导，得到

式中 T_s——钢丝绳中钢丝的拉力；

E_c——钢丝绳中钢丝的弹性模量；

ε——钢丝受到拉力后引起的应变；

F——钢丝绳的作用拉力；

ε_r——钢丝捻制过程的应变；

γ——钢丝绳恢复修正系数。

对于钢丝绳整体结构，可以通过对其分量参数进行求和得到，推导出钢丝绳中钢丝的弹性模量正值为

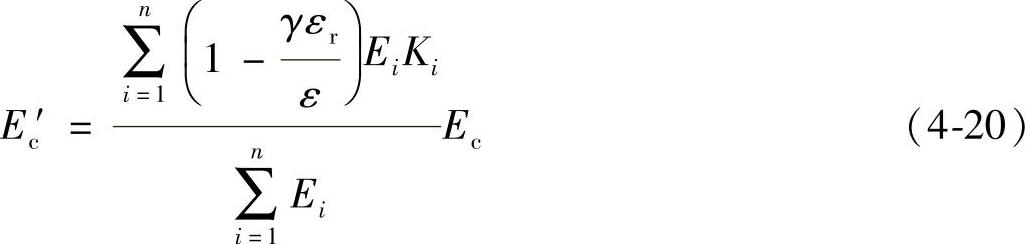
式中 E_i——序号为i钢丝的弹性模量；

K_i——钢丝弹性模量的修正系数，其具体计算式为

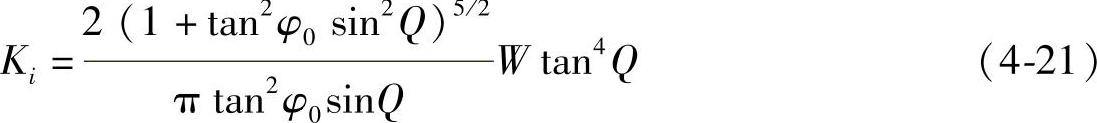
式中 W——角度的几何参考量，其取值在1.1～1.5之间；

φ₀——未进行调整的螺旋角。

根据式（4-10）所给出的单螺旋钢丝绳螺旋角与螺距的关系，进一步推导钢丝的变形后计算公式，研究截取单螺旋结构的一个螺距，钢丝螺旋角的变化可以根据下式确定

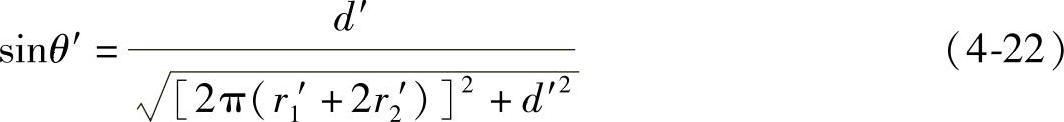
式中 θ′——变形后的螺旋角；

d′——单螺距受轴向拉力后新的长度；

r₁′、r₂′——变形后中心丝和螺旋丝的半径。(www.daowen.com)

结合钢丝绳单丝的几何形状及弹簧受力变形理论，得到轴向变化量公式为

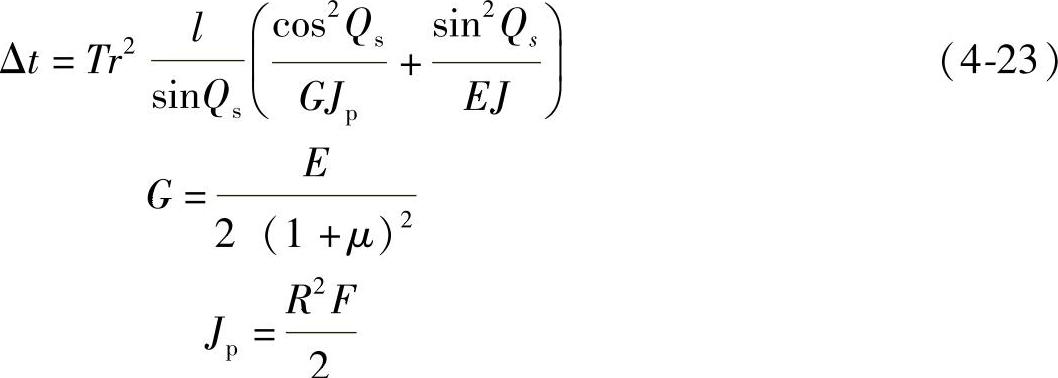
式中 Q_s——钢丝的一次螺旋角；

G——钢丝绳的剪切惯量；

J——钢丝绳模量的倒数柔量，下标p表示单螺距的柔量；

T——钢丝绳丝受到轴向拉力作用分量；

r——钢丝绳丝半径；

l——钢丝绳长度；

μ——钢丝绳单丝的泊松柏；

R——螺距空间半径；

F——钢丝绳的作用拉力。

进而钢丝应力状态表示为

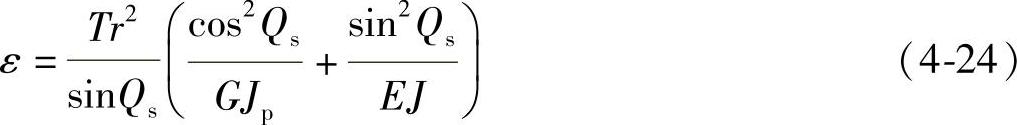
在受力情况下，钢丝本身因弹性效应能够略微伸长，但其变化量相对于结构上的伸长可以忽略不计，所以可以将钢丝的螺旋长度看作为常量，表示为 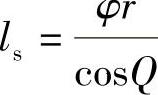，对其进行微分可以得到

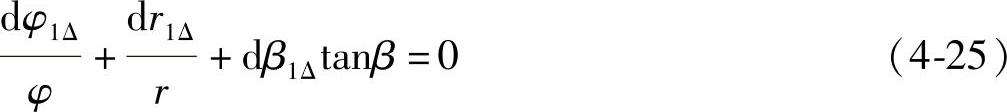
分开进行考虑，在仅考虑钢丝轴向旋转时，将钢丝绳长l=φrtanQ看作常数，对其进行微分可以得到

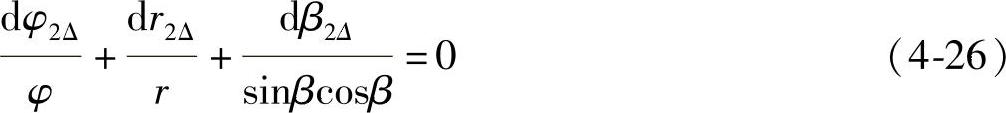
2.钢丝绳中接触应力计算

接触应力状态直接影响钢丝绳的使用寿命，常用钢丝绳各层股丝间的接触状态可分为点、线、面接触。在不同接触状态下，绳丝或绳股间的接触应力有较大的差别，其中点接触结构钢丝绳接触区的接触应力很高，接触点处磨损是该类钢丝绳破坏的主要形式；如果将点接触钢丝绳改为线接触，钢丝绳的工作能力可以提高25%，面接触钢丝绳的使用寿命则会更高[30]。

当钢丝绳受到轴向拉力时，钢丝或绳股有径向收缩趋势，使钢丝间及绳股间相互作用的径向力增加。当钢丝绳仅处于拉伸状态时，轴向拉力F_r、绳丝受力F_s及绳股受力F_g间的关系可以用作用力比值得出，用下式进行近似计算

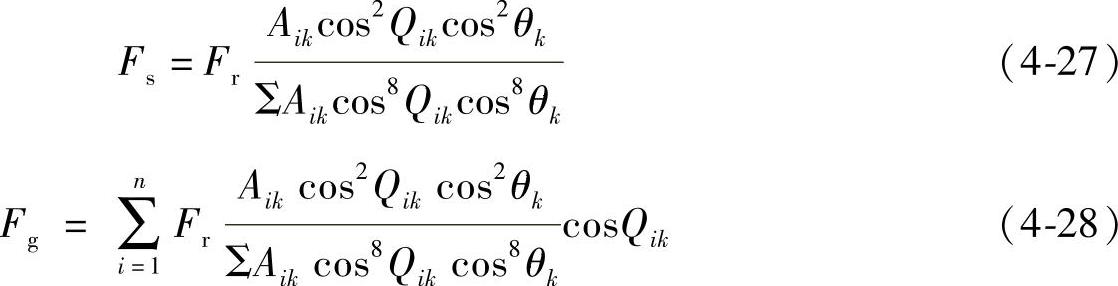
式中 A_ik——第k层股中第i根丝的横截面积；

Q_ik——第k层股中第i根丝的螺旋角；

θ_k——第k层股的螺旋角。

钢丝绳在轴向拉力及弯矩作用下的变形情况将在后面钢丝绳弯曲分析中进行研究。

进一步研究钢丝在受到轴向作用力后产生的挤压作用，从空间几何接触状态进行分析得到如图4-11所示的钢丝dl单元接触分布形式，其中dl单元在垂直轴线的圆周面上的投影长度可以用两个近似计算表示

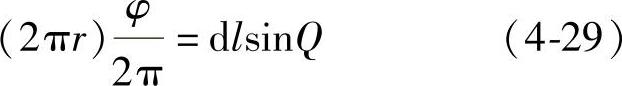
同时，将内部作用力在X方向和Y方向上进行分解，得到dl单元受总的载荷分布从钢丝绳芯指向钢丝绳外侧，大小为钢丝绳整体受力的sin²Q/r倍，如图4-12所示。

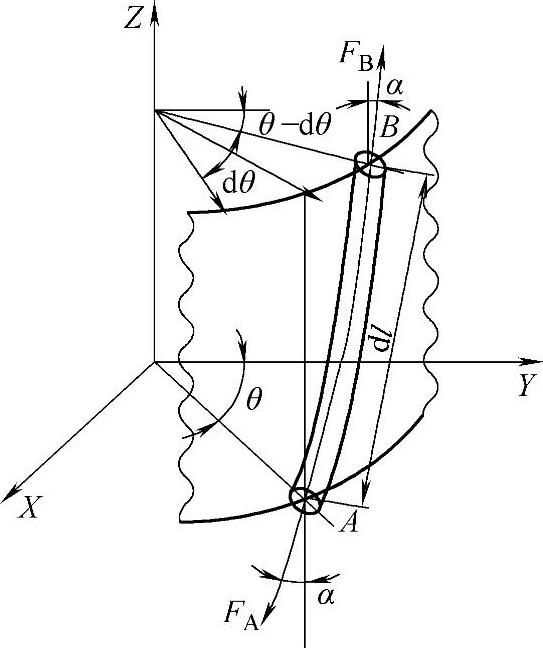
图4-12 钢丝在钢丝绳股中受力示意图^[31]

影响钢丝绳寿命的主要因素一直是研究钢丝绳的重要内容，通过大量的试验研究，人们发现，钢丝绳的使用寿命与其轴向作用力之间不存在明显的对应关系，而主要取决于钢丝或绳股间的接触作用力的大小、作用频率及累计时间。学者们通过理论结合实际的方法研究得出，钢丝绳在断裂之初形成的微裂痕主要出现在钢丝间微动磨损严重的部位，进而得到钢丝的主要损伤来自钢丝间的接触作用力。因此在设计钢丝绳过程中，人们提出增加钢丝间接触面积的设计方法，采用钢丝间面接触代替线接触，线接触代替点接触的设计方式，尽量降低钢丝间的接触应力，进而延长钢丝绳的工作寿命。

针对外股和绳股间的接触，在股芯钢丝数与外股钢丝数相同、钢丝绳与绳股同向捻制的情况下，两者之间的接触力可以通过获得的均布载荷乘以两个接触点间的距离得到，具体公式如下

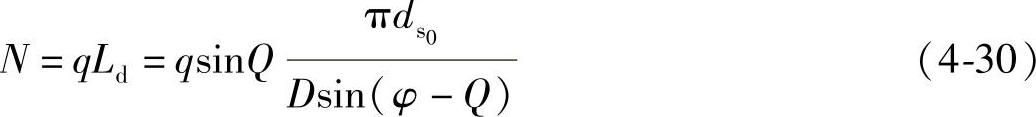
式中 q——均布载荷；

L_d——相邻两个接触点间的距离；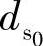

——绳股外侧相切圆直径；

D——接触外股的钢丝数。

针对同一层外股相互接触情况，相互间的接触力可以采用同样的方法用均布载荷乘以相互接触的长度，再除以该股中钢丝绳的数目得到。钢丝绳的破坏点主要位于接触滑动区，受到较高强度的接触、拉伸、弯曲应力作用，极容易形成微动磨损，进而缩短钢丝绳的寿命。

3.钢丝绳弯曲受力分析

在工程应用中，造成钢丝绳报废的主要形式有钢丝磨损严重、钢丝因腐蚀作用而变细及钢丝绳发生质变拉断等，其中前两种的终极结果都是第三种形式断裂。断裂也是引起重大安全事故的主要起因，所以在钢丝绳研究中，通常以防范钢丝绳发生突然断裂为主要研究对象。造成断裂的原因主要有钢丝绳长时间超负荷工作、钢丝绳受到腐蚀横截面降低达不到要求、在低温环境下工作钢丝发生脆化效应等。据统计，在钢丝绳突然断裂事故中，80%以上是因疲劳引起的，即钢丝绳在超负荷作用下，达到一定循环次数就会导致突发断裂事故，缩短钢丝绳的使用寿命。为此，工程实际中严禁钢丝绳在超负荷情况下长时间工作。

钢丝绳发生断裂需要经过三个发展过程：受到循环接触压力作用的钢丝表面出现微动磨损，微动磨损扩大形成裂纹初期，钢丝绳表面裂纹扩展形成疲劳受力状态发生断丝。

根据断裂试验发现，断裂常常出现在接触应力集中的钢丝绳表面，特别是钢丝绳受到弯曲应力作用时，最大接触应力发生在最外层钢丝的内侧。然而在实际工程应用中钢丝绳受到拉应力作用的同时有弯曲应力的参与，所以钢丝绳受力可以认为是拉应力和弯曲应力复合作用，同时钢丝绳在螺旋结构的作用下会出现扭转作用。因此，研究钢丝绳断裂的形成和发展需要将受力状态进行主次划分，才可避免应力集中，减少断裂事故的发生。

钢丝绳弯曲受力与钢丝绳的捻制及弯曲作用间存在直接关系，钢丝绳绕过绳轮形成弯曲接触面，作用力从接触面传递到钢丝绳外表面钢丝上，钢丝通过点、线或面接触将作用力相互传递，形成丝与丝、股与股间的接触作用力，如图4-13所示。由于钢股通常承受一定周期内的循环作用力，使其受力变形按一定交变频率发生。弯曲半径和弯曲直径大小不能小于特定钢丝绳直径的规定要求，该直径或半径过小将导致钢丝绳螺旋结构的破坏，使绳内绳股间出现结构性破坏，这种情况将大大缩短钢丝绳的使用寿命。

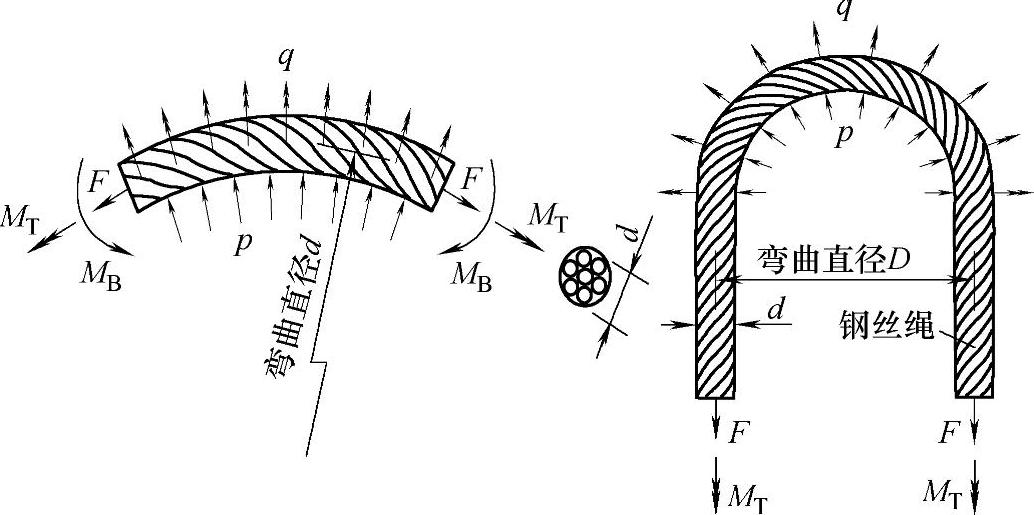
图4-13 钢丝绳径向受力示意图^[32]

根据提供的式（4-13）～式（4-30），计算得到弯曲钢丝绳受到轴向作用力曲线如图4-14所示，纵坐标为钢丝绳轴向作用力的变化，横坐标是钢丝绳在绳股中弯曲的位置。从计算结果中可以了解钢丝绳在弯曲过程中中心绳丝的受力情况，以及三次弯曲传递给中心及外侧绳丝的作用力分布情况。

通过试验得知，钢丝绳在常用的两种摩擦提升形式中会出现S型或U型的弯曲形式，两种形式的测试结果说明：S型提升机的钢丝绳寿命仅为U形提升机钢丝绳寿命的一半。研究发现钢丝绳在摩擦传动中的接触形式、承载力、曲率半径等因素对其使用寿命影响明显。假设钢丝绳的曲率半径为d，钢丝绳有效半径为r，d/r可以认为是其弯曲作用参数，该参数能够有效反应钢丝绳在弯曲中对自身损伤的大小，经过理论分析及模型计算，图4-15所示为钢丝绳受弯曲作用轴向受力分布图。

4.钢丝绳内部与外部的摩擦研究

从钢丝绳报废情况看，钢丝绳疲劳断丝主要发生在钢丝绳与滑轮接触部位及钢丝绳内部股与股间的接触点处。由于上面两种接触部位通常具有不同的曲率，导致接触时以点接触为主，同时钢丝绳在绕滑轮工作时，形成较高的接触应力，会使钢丝绳形成相对滑移并产生磨损。不同钢丝股内部钢丝间的接触可以分为点接触、线接触和面接触三种。通过计算，在载荷相同的条件下，点接触达到的最大应力值是线接触状态下达到最大应力值的5倍，是面接触的150倍。钢丝绳内部、外部接触中点与面接触会导致点接触部位被磨平，而点与点、线与线接触部位则首先发生挤压之后产生微动摩擦。

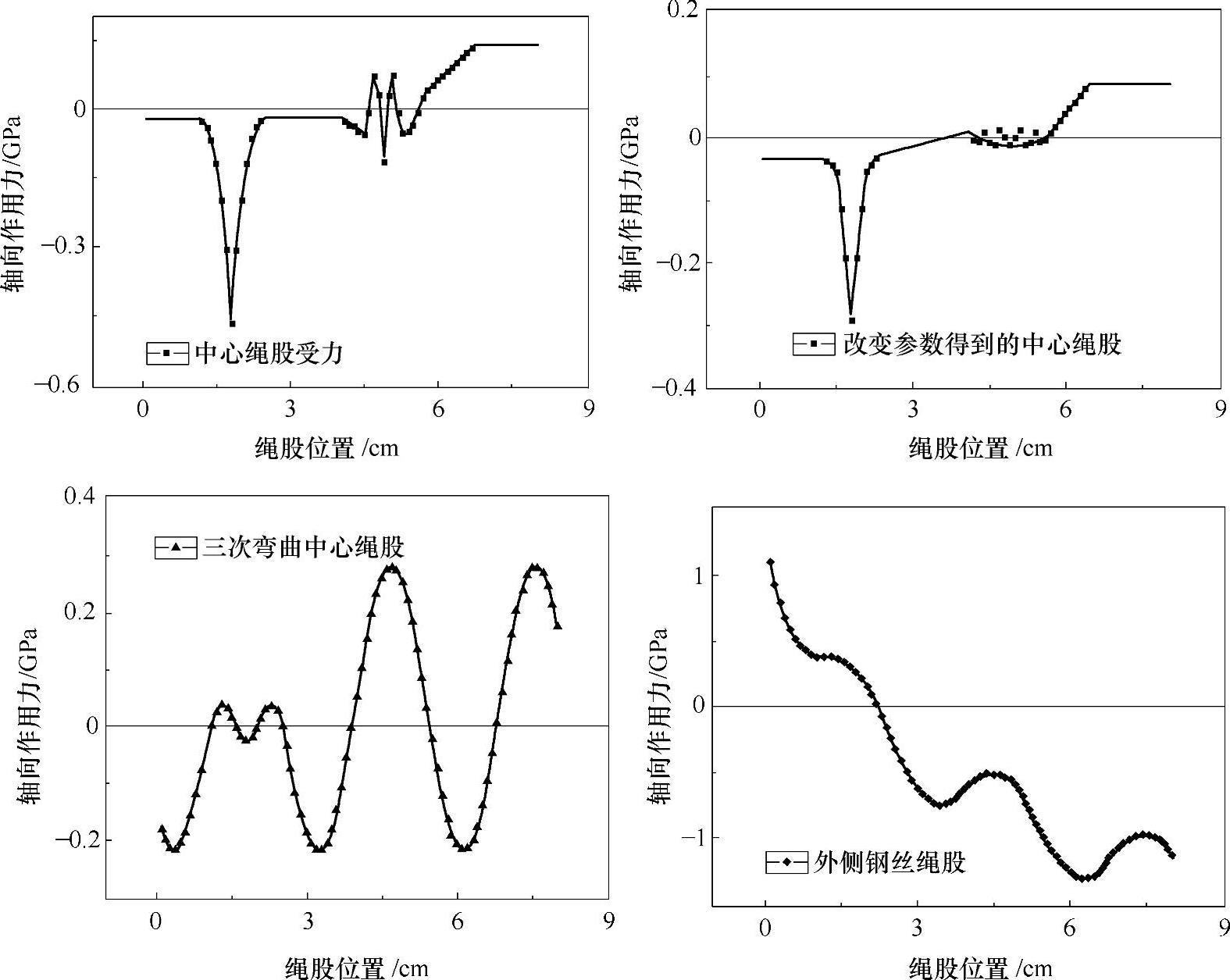
图4-14 弯曲钢丝绳受到轴向作用力曲线

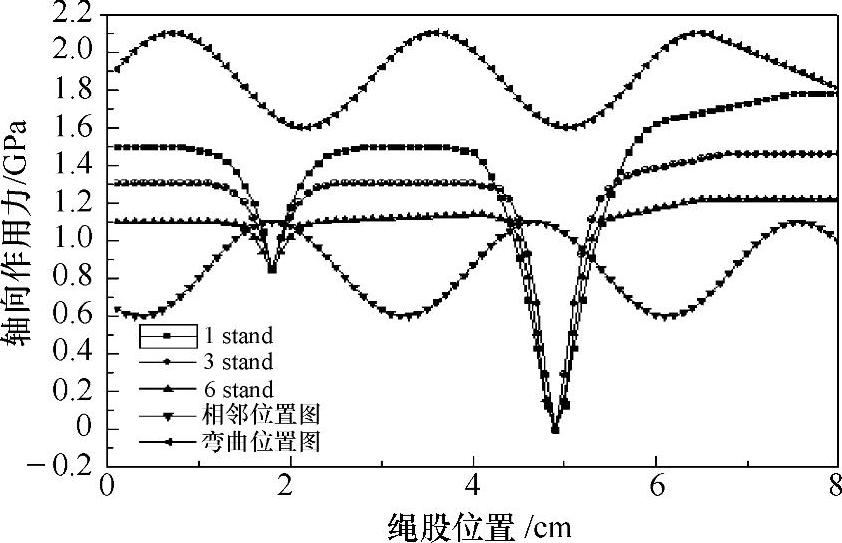
图4-15 钢丝绳受弯曲作用轴向受力分布图

基于接触弹性理论，假设带状接触位置的宽度为2b，接触中心最大压力为σ_max，其接触位置的压应力和剪应力分布规律如图4-16所示，最大剪应力τ_max发生在z=0.786b处，其值与压应力的关系为τ_max=0.3σ_max。当表面压应力增大时，位于表面下方的最大剪应力将容易促使钢丝表面形成微动磨损，进而形成点蚀破坏。

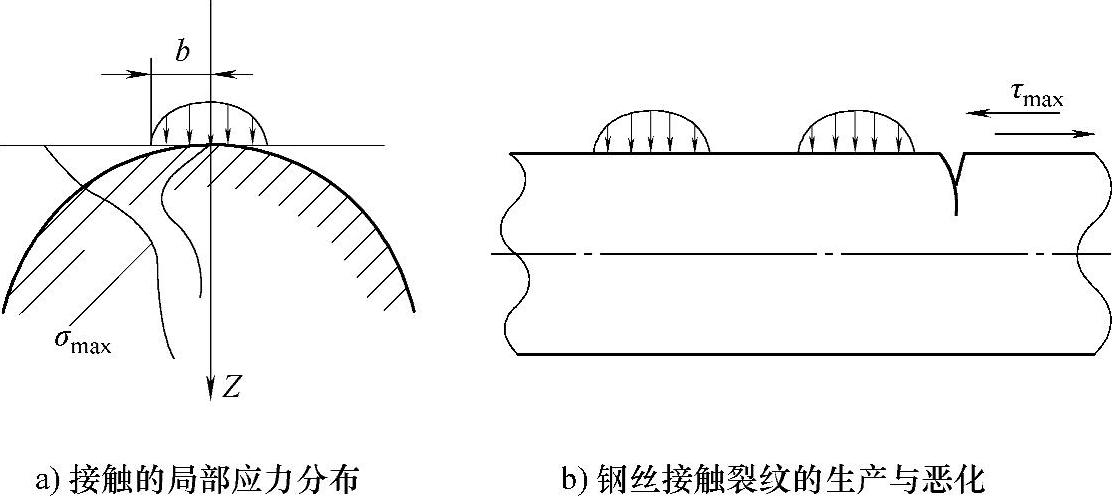
图4-16 接触位置的压应力和剪应力分布规律