钢丝绳内部呈现一种空间的螺旋结构,由螺旋丝经过捻制成股,绳股绕绳芯捻制构成钢丝绳,图4-1所示为钢丝绳构成示意图。
钢丝绳在不同工程中的应用决定钢丝绳选型、结构、原料和生产工艺。常用钢丝绳由直径为ϕ0.1~ϕ6.0mm圆端面的碳素钢丝捻制,特殊的密封和半密封钢丝绳则采用扇形或其他异型钢丝捻制。钢丝绳的类型按用途可分为悬吊桥梁用绳和矿用绳、架空索道用承载绳、传动装置用牵引绳、电梯用曳引绳、捆扎货物用系扎绳、航母甲板阻拦索用钢丝绳、精密仪器内传动绳等。为确保钢丝绳使用的稳定性和可靠性,要求钢丝绳有足够的强度、良好的挠性、捻制的密实性、抗压性、耐磨性、耐蚀性和抗疲劳强度等,其中使用过程中保证钢丝绳强度是众多性能中最为重要的。
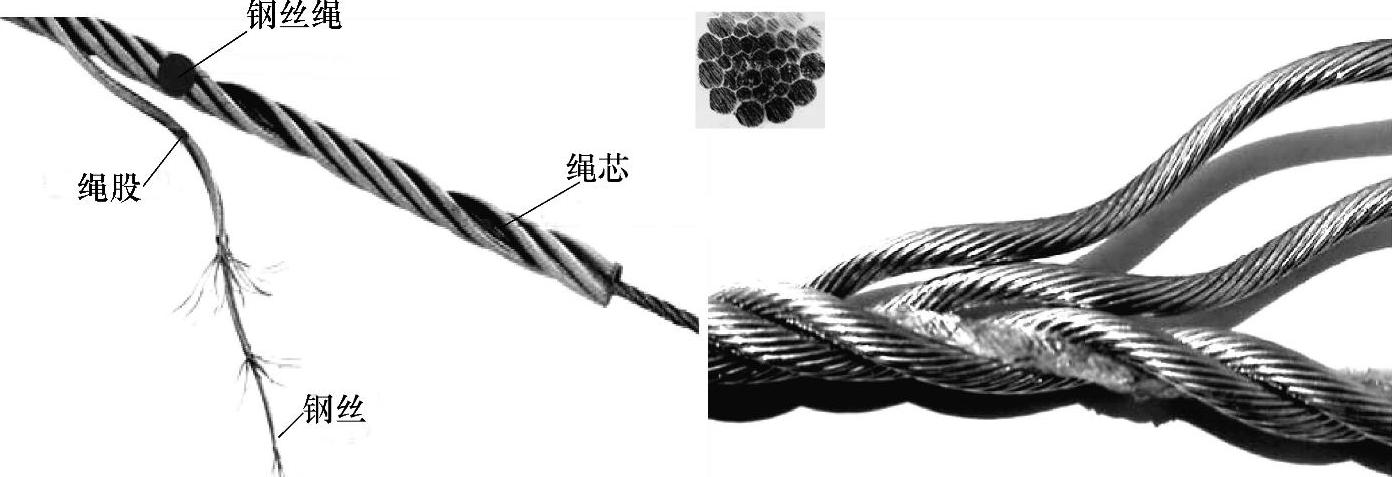
图4-1 钢丝绳构成示意图[23]
1.钢丝绳多螺旋结构数学表述
钢丝绳的结构模型是分析复杂钢丝绳在不同受力情况下结构变化的重要手段,结构模型是否准确将直接影响钢丝绳分析结果的可靠性。由于钢丝绳结构的复杂性,传统的分析方法主要依赖试验和工程数据,所以要获得特定条件下的可靠数据,需要以大量试验研究作为基础。获得的数据还依赖于检测设备的精度、检测材料的应用环境,而且获得相应的理论支撑也十分困难。因此,建立适合计算钢丝绳强度的结构模型一直是钢丝绳研究的基础。钢丝绳为多层螺旋结构,将钢丝或绳股绕直线丝或直线股旋转形成空间结构定义为单螺旋结构,将单螺旋中螺旋丝或股作为其他螺旋丝或股旋转的中心进行捻制旋转所形成的空间结构定义为双螺旋结构,以此类推可以出现三螺旋甚至更高的螺旋结构,从而增加了对钢丝绳结构分析的难度。
(1)单螺旋结构数学表达 单螺旋结构是钢丝绳最基本的组成形式,可用来表示螺旋丝之间形成的复杂几何关系。通过绳丝单螺旋捻制,可形成钢丝绳的绳股。借助微分几何理论可以准确地构建其几何表达式。为了便于分析,可将距中心丝不同距离的侧丝沿中心丝旋转展开成图4-2所示形式,图4-3所示为单螺旋结构空间几何模型。
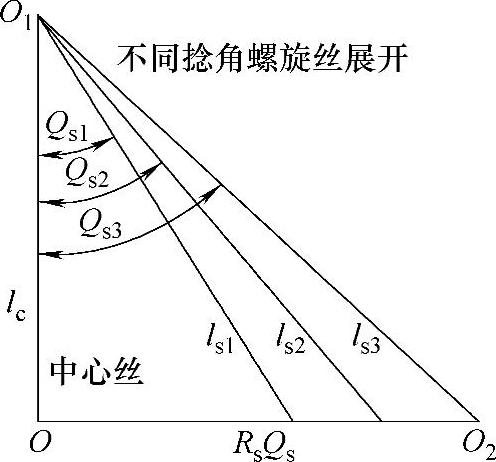
图4-2 中心丝及不同螺旋角钢丝沿捻向展开
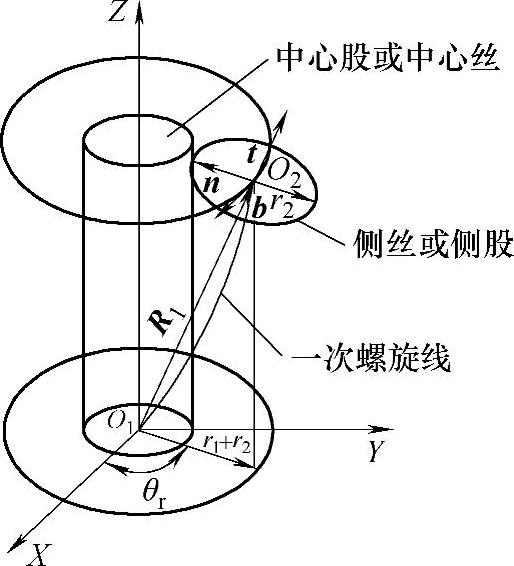
图4-3 单螺旋结构空间几何模型[24]
用lc表示中心丝长度,用ls表示股中的侧丝展开线长度,用Qs表示股中的侧丝捻角,用Rs为螺旋半径,用ri表示序号为i的钢丝半径。根据图4-2中的几何关系,其中螺旋丝lsi轴向应变εi与中心丝轴向应变ε及单位长度扭转角ϕ可以用下面公式近似表示
εi=εsin2Qsi+riϕsinQsicosQsi (4-1)
如图4-3所示,一次螺旋结构线上的点O2与结构中心点O1连线用矢量R1表示,R1的切向矢量定义为t,存在n与t垂直并指向钢丝绳的轴线,b与t、n构成右手系。θr表示一次螺旋丝的螺旋角。rs=r1+r2表示一次螺旋丝半径(补偿条件:内、外丝或股之间为接触的情况下)。基于平面几何理论可得到螺旋线平面方程为半径rs的圆方程
x=rscosθr
(4-2)
y=rssinθr
一次螺旋线的空间点坐标则根据捻制角的不同,以不同的角度沿平面圆的轨迹螺旋上升,其轨迹方程[13] 为
x=rscosθr
y=rssinθr (4-3)
z=rsθrtanQs
式中 tanQs——轨迹上升的斜率;
rsθr——随平面内圆轨迹变化的圆弧变化长度,该值是构成上升高度三角
形的底边长度。
式(4-2)最早由Costello提出并得到了多数学者的认可,Gordana M.Kastra'tovic、Cengiz Erdonmez、王大刚等均在此基础上建立钢丝绳的结构模型,并对其进行了相应的计算,获得了较好的分析结果。然而,对公式中各参数相互关系以及其对钢丝之间接触的影响,没有得到明确结果。
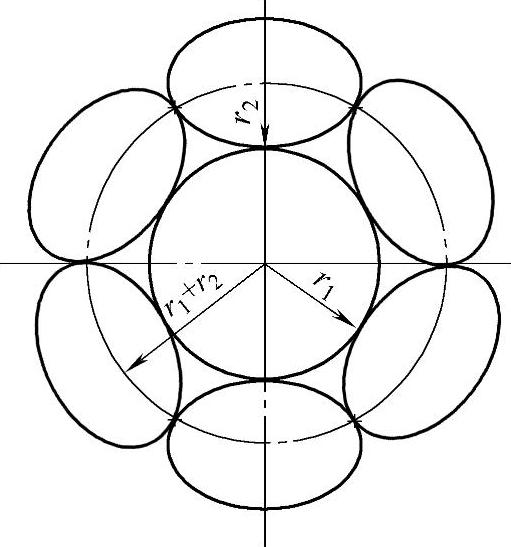
研究认为,单螺旋结构形成的绳股或绳设计中需要确定螺旋半径rs,绳丝半径r1、r2及螺旋角θr之间的关系,从而使绳丝和绳股内各部分形成较好的接触配合。这里所指的接触主要包括两部分:螺旋丝或螺旋股自身间的接触,螺旋丝与中心丝之间的接触。设定螺旋丝(股)数目用m表示,图4-4所示以m=6为例表示这种接触关系。
分析接触关系,可将螺旋丝形成的椭圆截面用方程表示为

式中 a——螺旋丝(股)的半径;
b——螺旋结构将圆形丝拉伸的椭圆长轴,b=r2/sinθr。
分析得到接触角β=π/m,具体位置如图4-4所示。假设已经确定内、外丝(股)的直径,求如图4-5所示内、外丝(股)之间均相切接触情况下的螺旋角。计算过程需列出外丝(股)间相交处切线斜率,方程如下

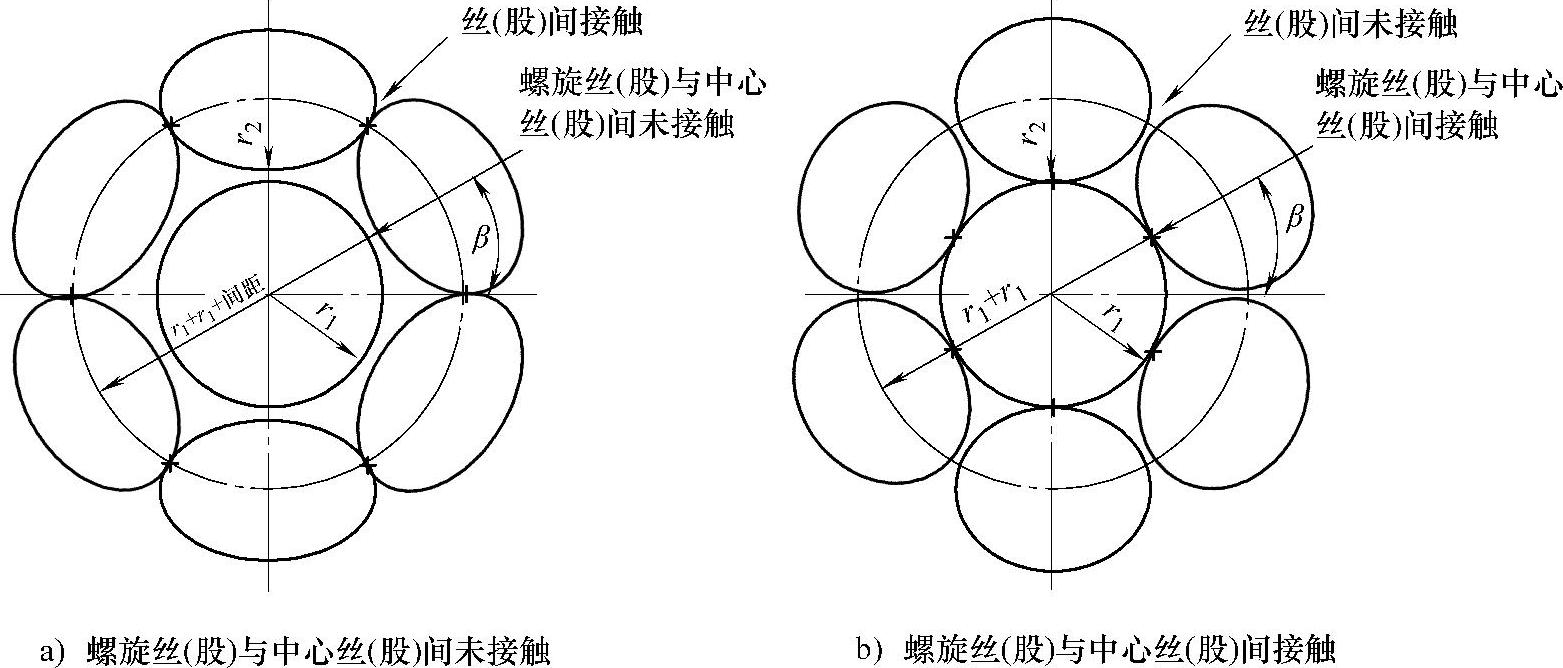
图4-4 螺旋丝(股)与中心丝(股)间接触关系[25]
切线方程
x=ytanβ=(a+r1)tanβ=b (4-6)
以中心钢丝绳为圆心,方程为
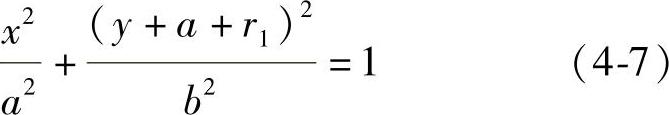
联立式(4-5)和式(4-7),其中已知β=π/m,a=r2,可以获得椭圆截面方程中的b值为
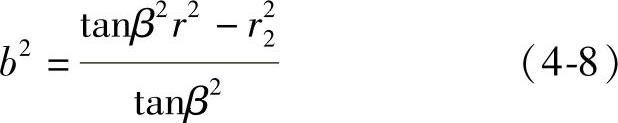
 (https://www.daowen.com)
(https://www.daowen.com)
图4-5 单螺旋结构 参数关系分析图
取正值,得外丝(股)螺旋后所形成椭圆截面长轴的长度,从而可以确定螺旋半径与钢丝(股)直径之间的相互关系。
式(4-7)与一维螺旋股侧丝未相互接触的判据式(4-8)具有相同的作用,只是推导的出发点不同
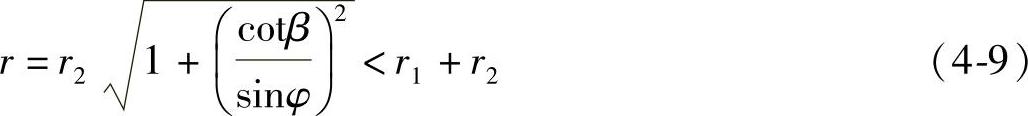
式中 φ——待求螺旋角。
与式(4-8)相比,式(4-9)具有更加直观、计算精度更高的效果。
示例:m=6,β=π/6=30°,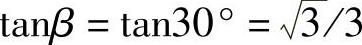 ,r1=1.7,r2=1.5,r=r1+r2=3.2,求外丝(股)的螺旋角;使外丝(股)之间以及外丝(股)与内丝(股)间正好相切时,外丝(股)形成的椭圆截面长轴b。
,r1=1.7,r2=1.5,r=r1+r2=3.2,求外丝(股)的螺旋角;使外丝(股)之间以及外丝(股)与内丝(股)间正好相切时,外丝(股)形成的椭圆截面长轴b。
根据公式计算可得b=1.868154,由于b=r2/sinθr,可知螺旋角的正弦值为

sinθr=r2/b=1.5/1.868154=0.802931,得到外丝(股)满足条件的螺旋角为θr=53.41°。
(2)双螺旋结构数学表达 基于单螺旋结构可以获得双螺旋结构表达式[26]
x=rrcosθr-rscos(θr+θs)
y=rrsinθr-rssin(θr+θs) (4-11)
式中 rs——一次螺旋丝半径;
rr——二次螺旋丝半径;
θs——二次螺旋丝的螺旋角。
根据三角函数展开得到下面的表达形式
x=rrcosθr+rs(-cosθrcosθs+sinQrsinθrsinθs)
y=rrsinθr+rs(-sinθrcosθs-sinQrcosθrsinθs) (4-12)
z=rrθrtanQ+rscosQsinθs
式中 Q——二次螺旋股的螺旋角;
Qr——二次螺旋丝引起螺旋股的螺旋修正角。
在双螺旋结构中同样出现上述螺旋角的问题,对不同直径的钢丝或绳股,如果其捻制螺旋角选择不当,将导致捻制过程中出现钢丝或绳股的挤压变形,如图4-6所示。通过计算调整螺旋角后的正常模型如图4-7所示。

图4-6 由于螺旋角选择错误出现的挤压模型

图4-7 调整螺旋角后的正常模型[27]
2.钢丝绳螺旋式几何模型的建立
根据公式可以建立钢丝绳二维螺旋结构模型,该模型充分考虑了钢丝或绳股间的相互接触状态,接近真实地建立了钢丝绳的结构模型,为钢丝绳受力分析打下了基础。建模过程分为五个步骤:
1)确定建模钢丝绳的参数,包括各层钢丝的直径及其螺旋角,如图4-8所示。其中螺旋角可以通过实际测量或根据上述计算方法确定,将这些数据作为给定参数赋给相应的变量。
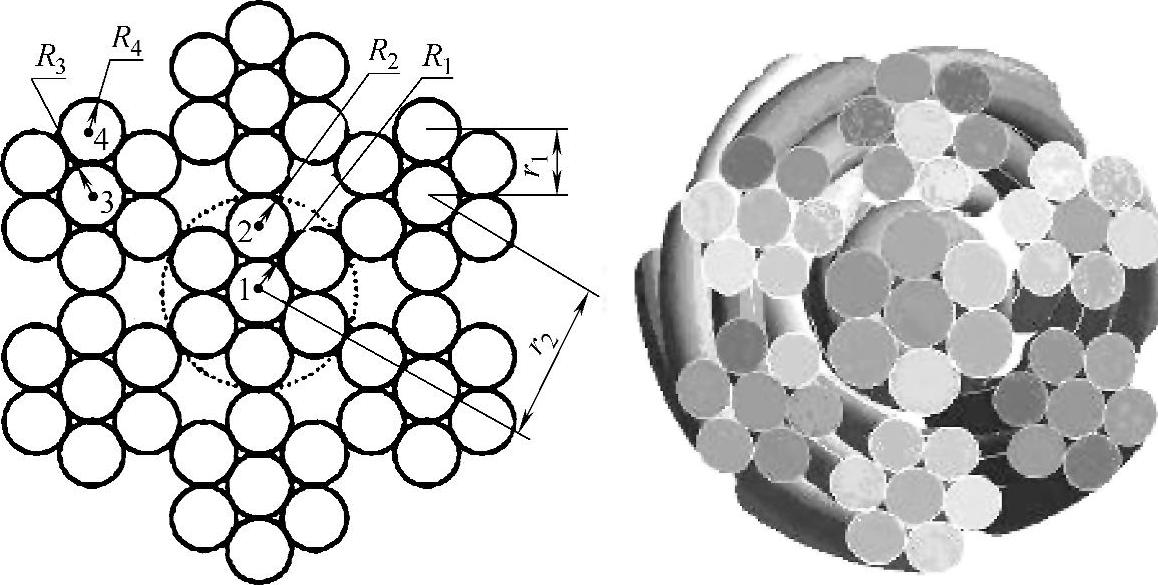
图4-8 IWRC7×7独立绳芯截面图
2)扫描出单螺旋丝的中心线,可以采用上述数学描述方程进行确定。在实际储存过程中,储存的是中心线上的关键点数据,这也是为了接下来形成圆形股弯曲钢丝提供基础附着点。在计算量允许的情况下,选择的计算点越多,中心线轨迹就越接近实际的曲率,所形成的IWRC7×7独立绳芯结构建模如图4-9所示。
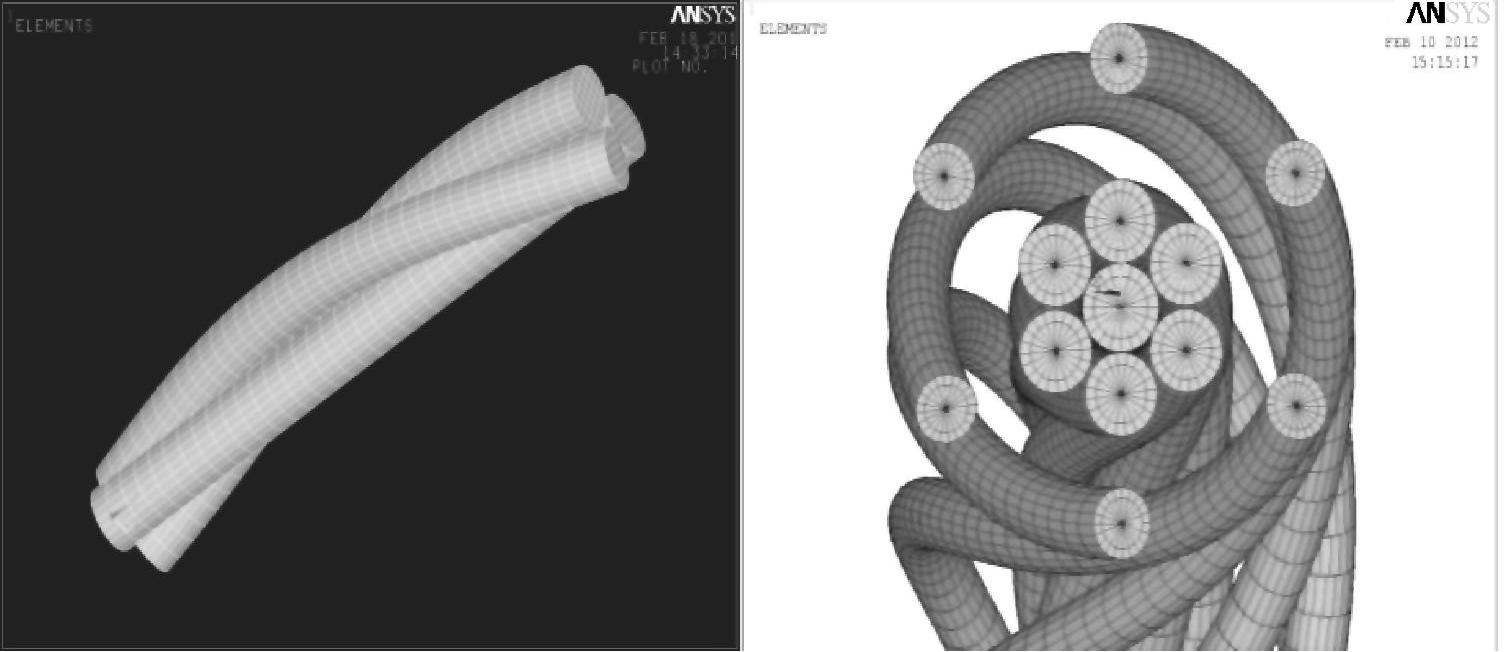
图4-9 IWRC7×7独立绳芯结构建模
3)将一维螺旋丝中心线作为基础线构建二维螺旋丝中心线,构建过程中主要满足二维螺旋数学方程式。由于不同位置螺旋丝具有不同的直径和螺旋角,所以要使建立模型中各丝的起点和终点相同,则需要进行细致的计算,这样钢丝绳绳丝中心骨架就完整地形成了。由于曲线较多,形成过程中应标记每条曲线的线号及其位置,以方便之后对其进行调取。
4)基于各个位置钢丝的直径建立截面,赋予相应位置的螺旋中心线,处理过程需要满足赋予截面与钢丝中心线处处垂直。
5)构建钢丝实体,检查各钢丝的相互接触状态,对参数进行细微的调整,最终完成钢丝绳的结构建模,如图4-10所示。

图4-10 IWRC7×19独立绳芯结构建模
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




