结构最优化设计日益受到建筑机械设计人员的重视。结构最优化设计的目的在于降低制造成本，改善产品外形，提高产品品质。其实质为一个数学优化问题，即确定一个或者多个设计变量的数值，使得目标函数达到最大值或者最小值，如结构的总质量最轻。这些解需要满足一定的约束条件，如杆件中的应力小于许用应力。

在结构力学中，可以精确分析一个承受给定载荷的结构而求得应力变形，却有可能不清楚应该如何布置和配置一个结构，使之有效地限制最大变形又能满足约束条件。利用ANSYS软件平台进行吊篮结构优化设计，在满足吊篮结构强度和刚度要求的情况下，对吊篮结构进行结构设计优化。在结构优化中，保证结构各个构件选用型材不变，以减小结构整体质量为主要目标，重点考虑2m护栏上竖腹杆和斜撑杆的数量和分布位置，减少结构材料的使用量，降低吊篮设计成本，提高U型高处作业装备的经济性。

在原始模型中，吊篮2m护栏上的竖腹杆数量为3，其与侧边立杆的最近距离为377.5mm，左右对称，如图3-68所示。为了研究如何布置竖腹杆的数量和位置才能使模型的质量最小，特提出优化方案进行对比。在保证各个构件选用型材不变的前提下，改变竖腹杆的数量和位置，分析它们的应力分布图，比较得出最优结构。优化目标是在满足吊篮结构强度和刚度要求的条件下，将2m护栏上竖腹杆的数量减少到2个，减小结构整体质量，同时调整竖腹杆的布置位置，减小结构最大应力和最大变形，如图3-69所示。优化参数如下：

目标函数：minWT（X）；设计变量：X（竖腹杆与侧边立杆之间的最小距离）；约束条件：0＜SMX＜107.5（最大应力）；0＜DMX＜10（最大变形）；0≤X≤1900。

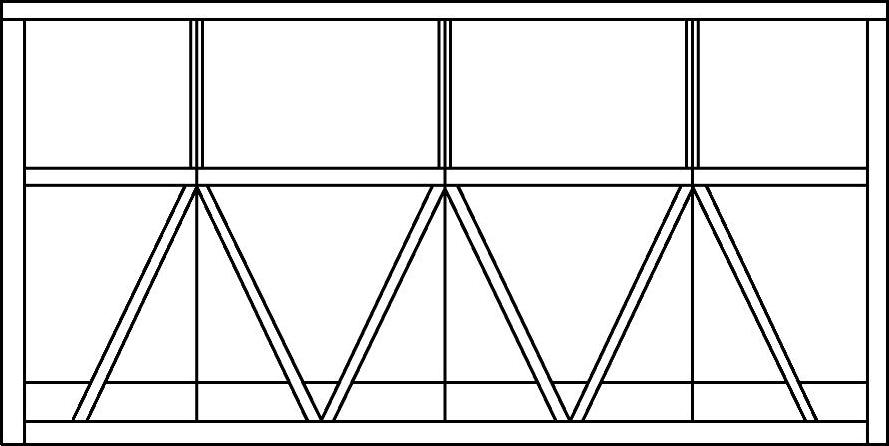
图3-68 吊篮模型2m护栏上的竖腹杆数量示意图

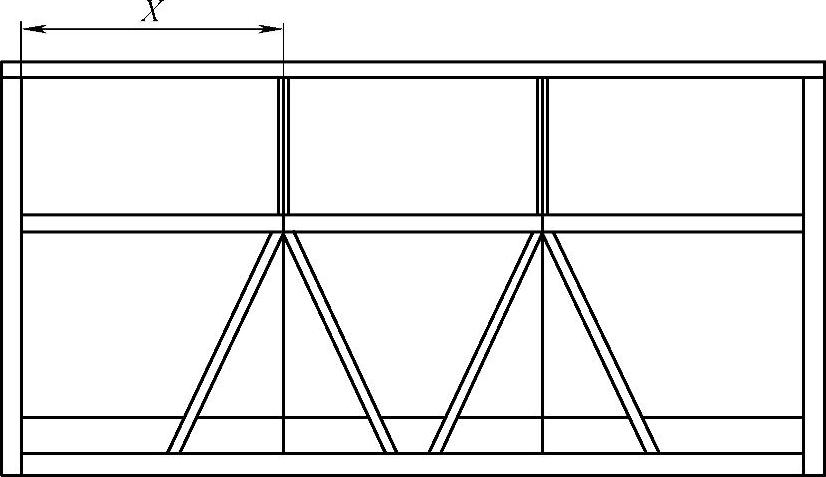
图3-69 优化后2m护栏上竖腹杆数量及位置示意图

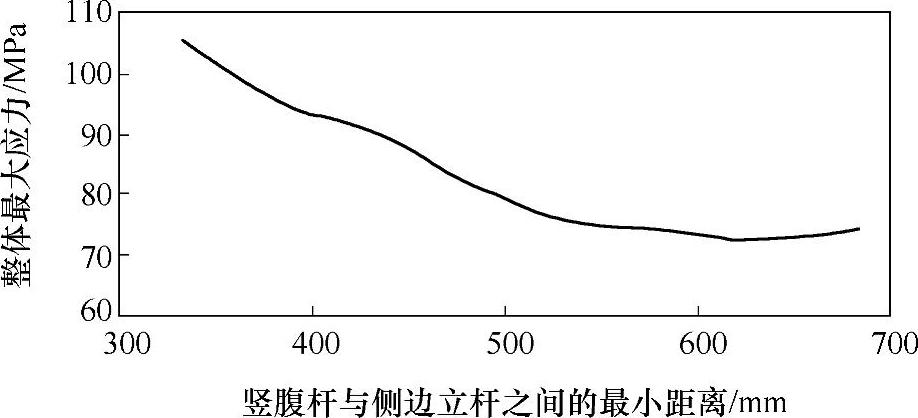
最大应力和最大变形等参数随竖腹杆位置的变化如图3-70和图3-71所示。

从图3-70和图3-71可以看出，随着竖腹杆与侧边立杆之间最小距离的增大，吊篮整体结构所受的最大应力和最大变形渐渐减小。当其达到一定值时，所受最大应力和最大变形开始增大，但都在许用应力和许用变形条件范围内。为了得到最优结构，既要限制最大变形，又要减小最大应力，最大应力和最大变形随竖腹杆位置变化分析结果见表3-12。

(www.daowen.com)

图3-70 最大应力随竖腹杆位置的变化

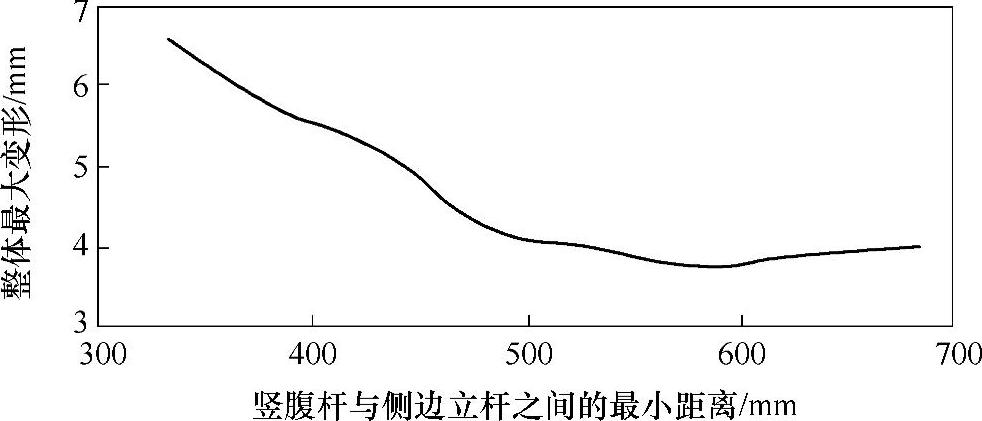
图3-71 最大变形随竖腹杆位置的变化

表3-12 最大应力和最大变形随竖腹杆位置变化分析结果

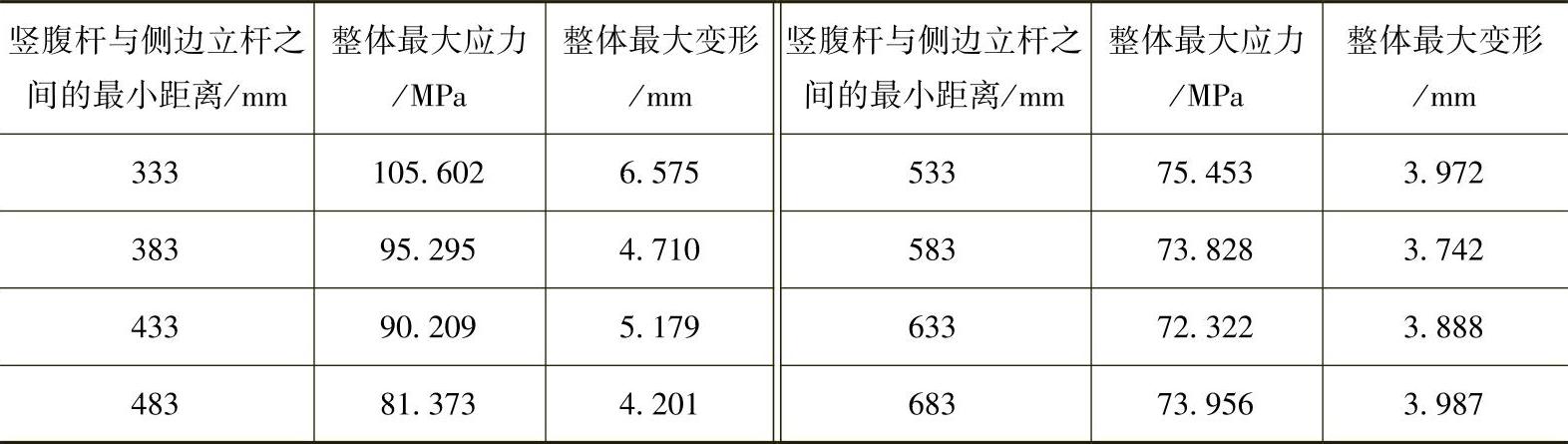
根据表3-12中的分析结果，得出优化结构为2m护栏上设置两个竖腹杆，竖腹杆与侧边立杆之间的最小距离为633mm，整体结构所受最大应力为72.322MPa，最大变形为3.888mm。原始吊篮模型2m护栏的质量为23.8kg，优化后的质量为21.61kg，在满足应力应变约束条件下质量减少了9.2%，整体结构质量降低了2.1%，节约了工程材料、减少设计成本，使结构设计更为经济、科学、合理，达到了优化目标。图3-72和图3-73所示分别为U型平台结构优化前后的模型对比。

图3-72 U型平台结构优化前模型

图3-73 U型平台结构优化后模型