在实际应用情况下，结构受到的载荷作用总是随时间变化着，当动载荷在所有载荷中不占主导地位时，动载荷的影响可忽略不计，只需做静态分析计算。但仍有结构受到显著的动载荷作用，如船舶受到海浪冲击的作用、桥梁受到车辆冲压的作用等，在这种情况下就必须进行动力学分析。还有些结构虽受动载荷作用影响的效果不明显，但由于载荷的频率和实际结构的某一阶固有频率接近，就会使结构引起显著的振幅变化，同时在其内部产生较大的动应力，从而使结构受到破坏或产生不应有的变形，在这种情况下也应该进行动力学分析。本章运用ANSYS软件对U型高处作业平台进行动力学分析。

1.U型平台模态分析

U型平台结构的振动频率对整个高空作业平台的性能有重要的影响。在使用过程中，振动不仅会造成U型平台结构的疲劳破坏，而且会产生一些共振和噪声，因此对U型平台进行模态分析是很有必要的。

U型平台模态分析具体过程：

（1）U型平台模型的建立 在分析中，模态分析的模型可以与静力学分析相同，因此本章采用静力学分析时所用的模型。如图3-60所示为U型平台的有限元模型的俯视图，依据第2章对吊点分布的分析，将平台分为A、B、C三个区域，A区域为平台上端2m标准节，B区域为平台下端2m标准节，其余部分为C区域。

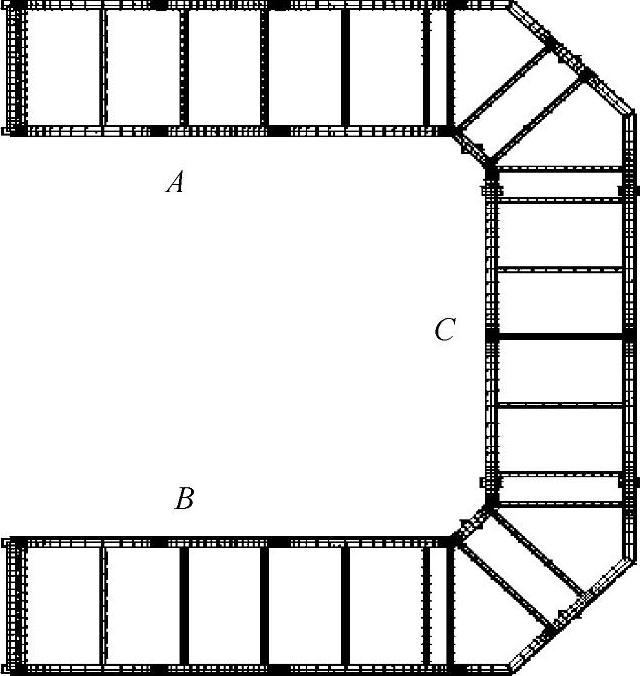
图3-60 U型平台的有限元模型的俯视图

（2）对U型平台模型加载并求解 在模态分析中，有效载荷是零位移约束，在某个DOF位置制定了非零位移约束，那么程序自动会以零位移约束替代该DOF处的位置。即使在模型中施加其他形式的载荷，在分析时这些载荷也将会被忽略掉。在这一步对U型平台模型设置分析选项以及分析类型，对模型施加载荷，并指定加载阶段选项，最后求解固有频率。

（3）扩展模态并查看分析结果以及后处理 本章只对U型平台系统结构前六阶模态进行了求解。

运用ANSYS分析软件对U型平台CAE模型进行自由模态处理后，得出了U型平台前6阶固有频率，系统结构的固有频率分析结果见表3-11。

因为该U型平台的结构较大，其振动频率较低，结构动态响应中，低阶模态占主导地位，高阶模态的影响较小，随着阶数的增加，影响就越小。介于系统结构阻尼的影响，响应中高阶模态部分衰减速度也较快，因此可以对高阶模态忽略不计。本章在模态分析过程中，只选取前六阶固有频率进行分析。

表3-11 系统结构前六阶的固有频率分析结果

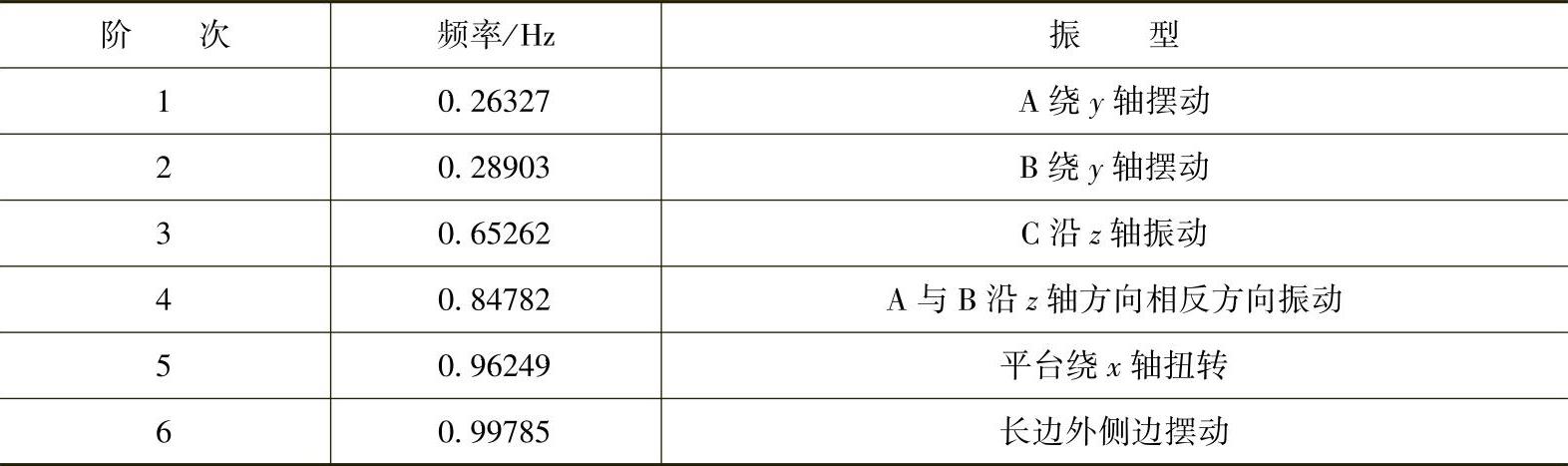
从表3-11可知，当外界的激扰频率与表中的数值接近时，很有可能使U型平台产生较大的振幅，使结构受到一定程度的损害。因此，在设计过程中，如果知道外界激扰频率，可通过修改设计参数改变结构振动频率范围，避开外界激扰频率，从而降低不应有的振动，以提高平台整体结构的稳定性和安全性。

2.U型平台的谐响应分析

谐响应分析用于确定结构在受到随时间按正弦规律变化的载荷作用下的稳态响应的一种技术，其目的是计算系统结构响应随频率变化的曲线。谐响应分析也是一种线性分析，可以有预应力结构。其分析过程主要由三个步骤组成：建模，加载并求解，观察结果及后处理。本节内容是在U型平台模态分析基础上，计算平台结构在前六阶固有频率的范围内，承受单位简谐载荷的位移响应曲线。

根据模态分析可知，在U型平台动态响应中，低阶模态占主要地位，高阶模态产生的振幅很小，并且由于系统结构阻尼的影响，响应中的高阶部分衰减速度很快。因为进行谐响应分析时必须指定频率范围，而且U型平台结构的频率较低，故只需要考虑0～5Hz频率范围内的结构响应情况。在此过程中，载荷的实部为1，虚部为0，载荷的方向选择F_y，在此基础上进行求解分析。

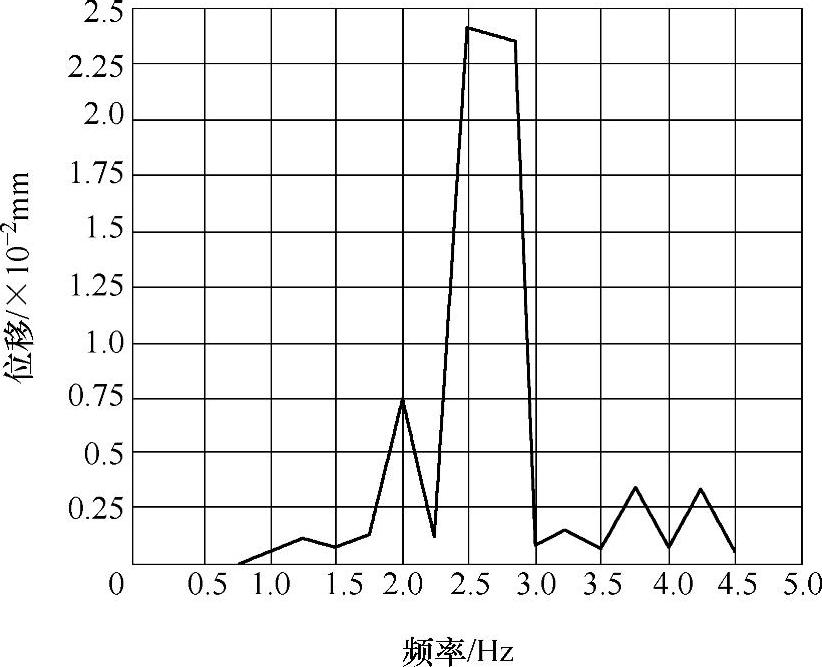
图3-61 U型平台护栏响应 位移随频率变化曲线(www.daowen.com)

由于U型平台整体结构节点较多，为几十万个自由度的较大型系统，如果要对所有节点求解是比较困难的。因此，选取在U型平台的护栏、底架以及平台与安装架连接点处进行取点计算。各所取节点的响应位移随频率变化曲线如图3-61～图3-63所示。

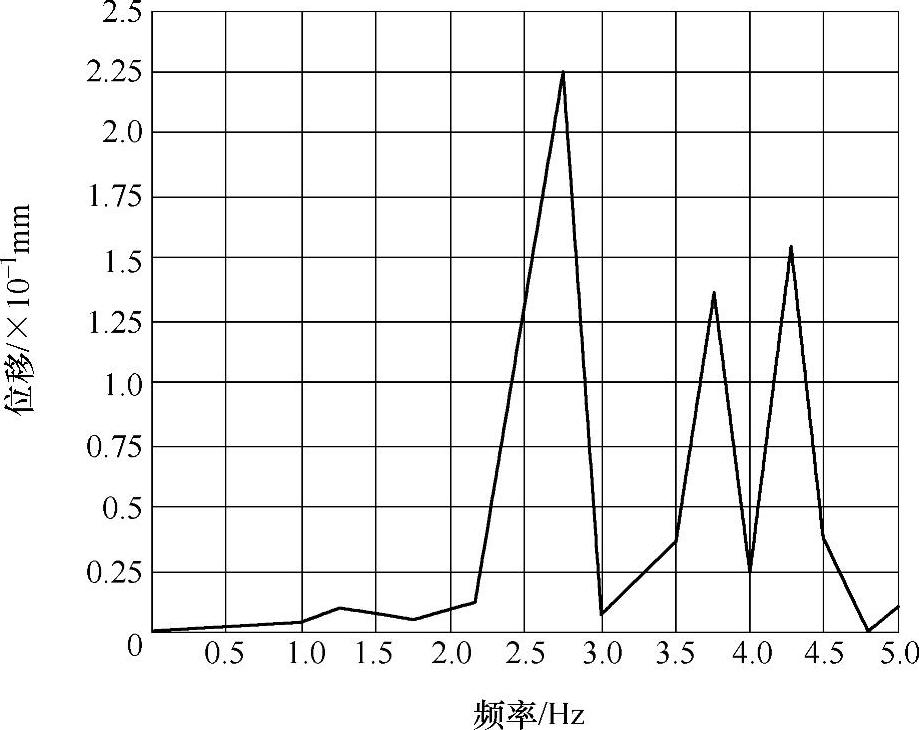
图3-62 U型平台底架响应位移随频率变化曲线

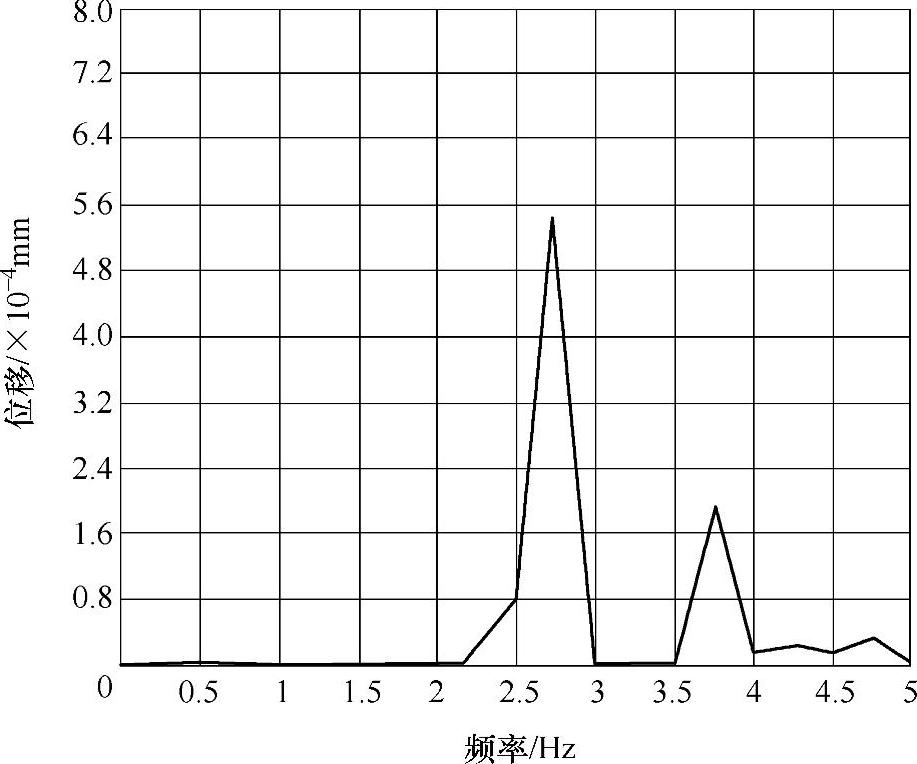
图3-63 安装架连接处节点响应位移随频率变化曲线

从图中可以看出，在底架节点的响应位移最大，在平台与安装架连接处节点的响应位移最小。在结构动力学中，当外界载荷激振频率与系统结构固有频率相近时，会发生结构共振现象，此时的位移响应最大。从不同节点处响应位移随频率变化曲线可以看出，当激振力的频率在2.0～3.0Hz区间时，节点处的响应位移突然增加，并在该区间迅速达到一个峰值，然后急剧下降回复到之前状态。从以上数值可以确定，激振力的频率在2.5～2.75Hz区间时，容易发生共振现象。在实际施工过程中，主要模态方向的干扰力、起升机构起制动等原因引起的激振力，都将影响U型平台工作时振幅的大小，因此应尽量减少这些因素带来的不良影响。

3.U型平台瞬态动力学分析

U型平台在使用过程中，瞬间起升和突然停止都会产生较大的冲击载荷，这些冲击载荷对整体结构的影响较大，因此，很有必要对U型平台进行瞬态响应分析。根据U型平台设计参数可知，平台的额定载重量为5000N，起升过程中产生的冲击时间在1s内完成，图3-64所示为载荷简化时呈曲线。在ANSYS中，瞬态分析的求解精度与积分时间步长有关，因此应当根据一定计算准则，得出最优时间步长。由于U型平台计算模型比较大，在前面已经得出的模态分析结果基础上，再次确定积分时间步长为Δt=0.5s，并且将其划分成20个子步，从而满足直接积分的稳定性要求。

通过前面对U型平台的静力学分析、模态分析和谐响应分析，基本上可以确定在整个U型平台结构中，其危险点位于底架以及底架与安装架连接点处。所以在瞬态动力学分析中，选取谐响应位移值中最高点为分析节点。对U型平台计算模型起升冲击荷载进行瞬态动力学求解，从而获得U型平台底架上危险节点处的动态响应时间历程。如图3-65～图3-67所示，它们分别为该节点在受到起升冲击载荷后的X向、Y向、Z向位移变化曲线。

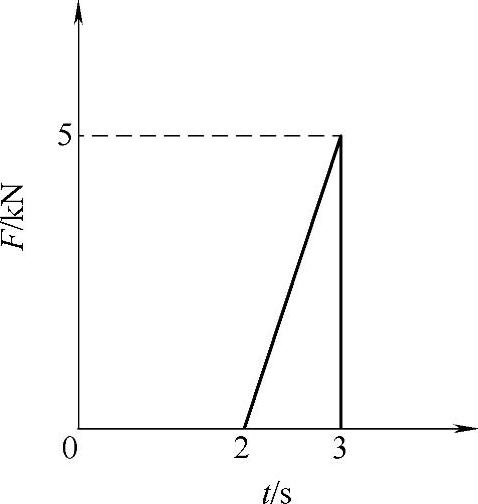
图3-64 载荷简化时程曲线

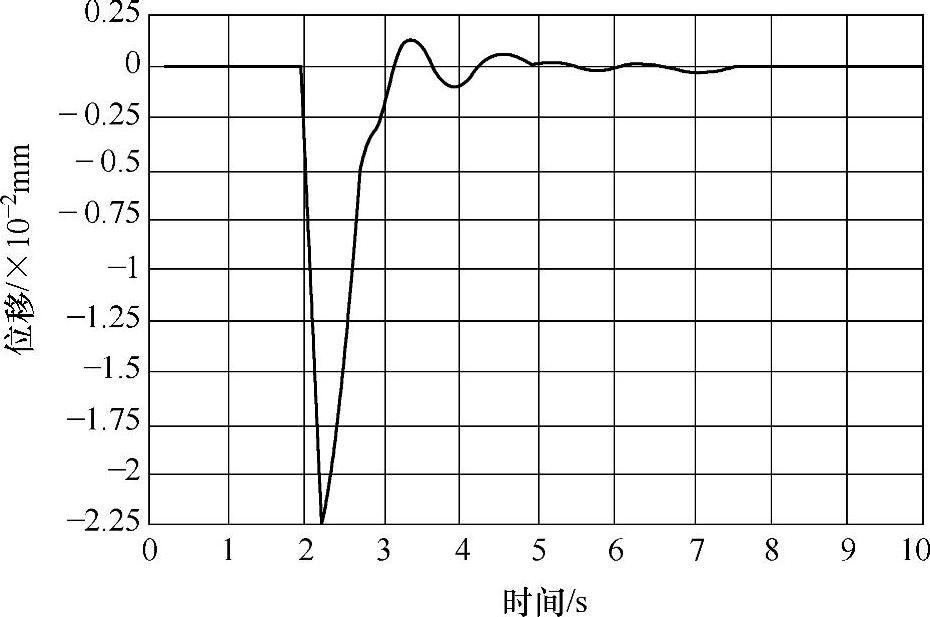
图3-65 X方向位移变化曲线

由以上各图可以得知，瞬态振动期间，各方向的振动位移衰减速度较快，在X、Y、Z向位移中，Y方向振动位移衰减最快，最大位移响应值为0.22mm。所以在U型高处作业平台进行满载施工运行时，施工人员要控制好平台起动和制动时的速度，从而避免在平台施工运行过程中出现瞬时起动或者紧急制动而造成的结构变形，甚至导致破坏。瞬态动力学分析结果对U型平台运行的平稳性、安全性以及使用寿命都有着重要的意义。

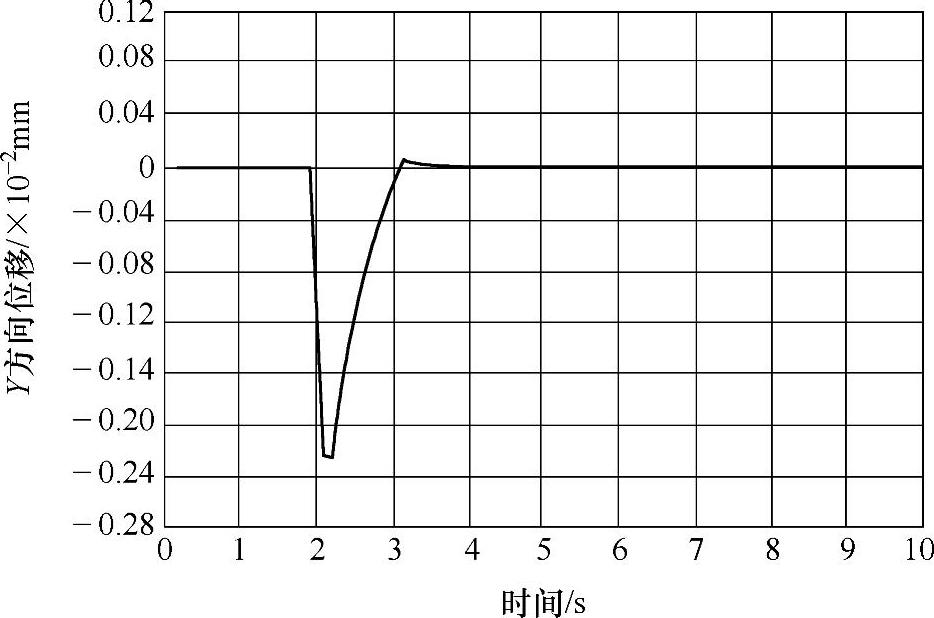
图3-66 Y方向位移变化曲线

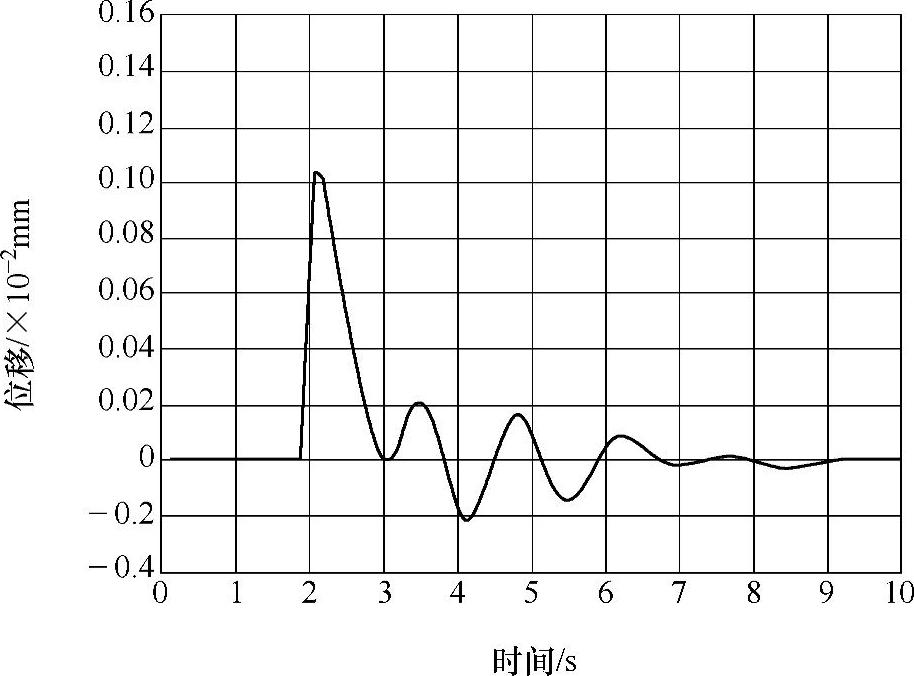
图3-67 Z方向位移变化曲线