起重机械的动载荷是由于质量系统运动状态的突然改变而产生的动力载荷。在突然起动和制动时，由于系统属于弹性系统，会造成起重机械系统出现弹性振动，故产生动力载荷。对于金属结构和支撑零件，当起升机构工作时，被提升的重物突然离地或下降时突然制动，就会产生这种动力载荷。如图3-24所示为悬吊平台起升过程中钢丝绳拉力变化示意图^[17-20]。

悬吊平台在起升过程中，当平台处于突然起升或下降工况时，钢丝绳承受的载荷既包括悬吊平台及重物所产生的静载荷P_静，还包括突然起升过程中产生的惯性载荷P_惯。由静载荷和惯性载荷构成了其基本载荷。由于钢丝绳属于弹性构件，除了以上基本载荷外，还在钢丝绳上叠加了按一定频率变化的振动载荷P_振，振动载荷与上面两种基本载荷的共同作用使钢丝绳内部应力峰值大大提高，而且由于振动载荷的作用，设备的某些敏感部位将发生疲劳破坏。因此在金属结构和传动零件的强度计算中，最大工作载荷以最大振动载荷为依据。为了便于计算，起重机械中通常用动载系数φ来表示动载荷的大小。动载系数的定义是最大振动载荷P_max与静载荷的比值，对于传动零件则是最大振动载荷力矩与电动机额定力矩之比，对于金属结构和支承零件

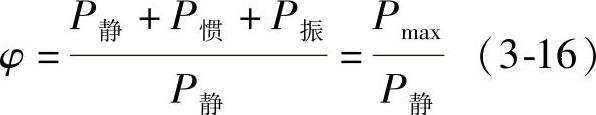
式中 φ——动载系数；

P_静——静载荷；

P_惯——惯性载荷；

P_振——振动载荷；

P_max——最大振动载荷。

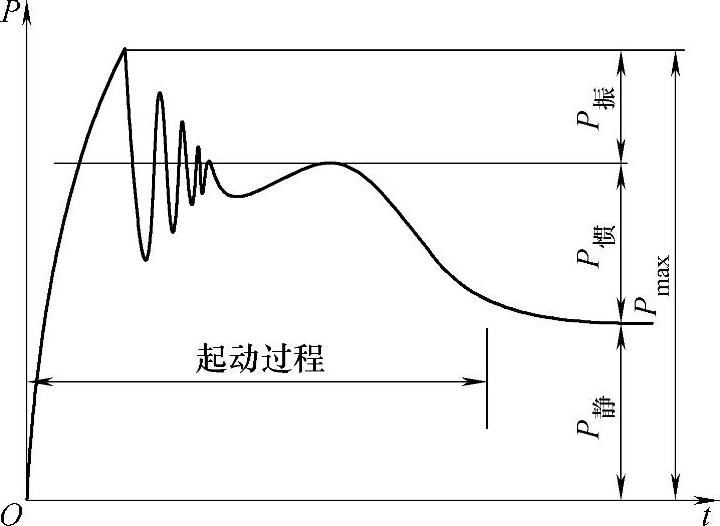
图3-24 悬吊平台起升过程中钢丝绳拉力变化示意图

建立高空作业施工装备中悬吊平台突然离地起升的动力学模型步骤：

1）画出高空作业施工平台的力学模型简图，明确主要构件的受力关系。

2）确定各主要部件的参数。

3）通过力学模型简图来建立动力学研究的数学模型（描述系统运动的微分方程）。

绘制力学模型的简图主要考虑两个方面：首先要抓住机器或机构的特点，其次，还要遵循所求解问题的各项指标。一方面，简图要能够真实地反映机器工作时最本质的物理过程，及分析者关心的关键点的振动情况。另一方面，研究问题时不能一味地追求高精度，还应与研究人员的计算工作量进行合理的分配，过于精细的力学模型将影响求解速度，甚至造成无法求解。因此，以上两个方面的因素均应予以综合考虑，系统的坐标位置和自由度数也应依据以上两个因素选取。一般情况下，模型的自由度数越多，所获得的结果精确度也越高，但同时计算工作量也越大，甚至使解题发生困难。自由度数的选择在很大程度上取决于已有的类似机器和结构的分析计算及试验数据的分析。一般来说，系统的自由度数不应小于对响应具有决定影响的固有振型数。

高空作业施工装备中平台不是绝对的刚体，而是一个多质量、多自由度的弹性振动系统，但是如果把施工平台看成弹性振动的问题进行分析，会导致问题的复杂化。

首先，施工平台的弹性系统是由多个惯性质量（如悬吊平台、提升机、起升钢丝绳及所提升的重物）以及弹性构件（起升钢丝绳、悬挂机构悬臂梁及悬吊平台底板）联系起来的，有些构件的质量还是不均布的。因此，它是一个多自由度的振动系统，研究时要解多元联立微分方程，要求解精确解具有一定困难，且求解过程非常复杂。

其次，施工平台工况较多，所受载荷又随着起升高度、作业人员位置等变化而发生变化，当悬吊平台突然离地起升，引起结构振动时还会对外载荷产生一定的影响，对施工平台的起升系统进行精确的动力计算具有一定的困难。近几十年来，虽然结构振动理论得到了不断发展和完善，对多质量、多自由度的力学-数学模型进行计算已不再是难题。但由于大量的系数和参数无法求出，计算形式过于复杂，大大降低了使用价值，而且不容易反映问题的物理本质，所以目前仍然趋向于采用简化模型计算。

当悬吊平台离地起升时，整个起升系统受到较大的冲击，弹性变形主要集中在起升钢丝绳和悬挂机构的悬臂梁，这种结构与钢丝绳串联的系统可以简化为单自由度弹簧质量系统。其中k_eq为悬挂机构悬臂梁刚度与起升钢丝绳刚性系数的等效刚度，m_eq为悬挂机构在钢丝绳悬吊点处的等效质量与起升质量的等效质量。图3-25所示为单自由度弹簧质量系统动力学模型。

单自由度系统的振动运动微分方程为

式中 m——质量（kg）；

x——位移（m）；

c——阻尼系数；

k——弹簧弹性系数。

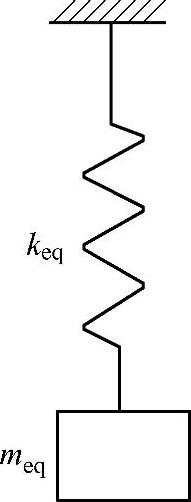
图3-25 单自由度弹簧质量系统动力学模型

结合实际工况，可以发现对起升机构最不利的情况是：满载状态下开动提升机使悬吊平台从地面急速起升，当操作者操作不熟练或者不仔细，有可能在钢丝绳松弛的状态下以很高的速度将悬吊平台由地面突然提起，这一过程会产生较大的动力载荷。应当对这种情况进行分析计算。

（1）单自由度系统动力学模型法计算悬吊平台的冲击载荷 将模型简化为单自由度系统进行计算。

系统的等效刚度系数为

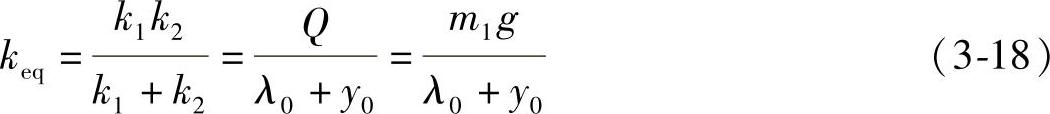
式中 k₁——悬挂机构悬臂梁等效刚度（N/m），其大小与张紧钢丝绳的预应力有关，预应力越大悬臂梁刚度越大，其值约为k₁=723122N/m；

k₂——钢丝绳刚度（N/m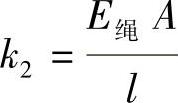），，其中E_绳=120GPa，A=58.088mm²，l=100m得k₂=69705.6N/m；

g——重力加速度（m/s²）；

m₁——起升质量，包括平台质量、额定载重量、钢丝绳质量，当额定载荷均布时，m₁=（m_台+m_额）/2+m_绳=（650+800）kg/2+40kg=765kg；当额载偏置作用时，m₁=m_台/2+3m_额/4+m_绳=1/2×650kg+3/4×800kg+40kg=965kg；

λ₀——钢丝绳在额定起升载荷Q作用下的静位移；

y₀——悬挂机构悬吊点在额定起升载荷Q作用下的结构静挠度。

系统等效质量按如下能量方程求得

式中 m₂——悬挂机构在悬吊点处的等效质量，m₂=13.872kg。

代入相关参数，计算得额定载荷工况下的冲击载荷为P_额冲≈1043N，额定载荷偏置工况下的冲击载荷为P_偏冲≈1174N。

（2）运用能量方程法计算起升冲击载荷 具体的能量方程为冲击动能=弹簧势能，即

式中 P——冲击载荷（N）；

v₀——起升初始速度（m/s）；

m——起升质量，包括平台质量、额定载重质量、钢丝绳质量（kg）；

k——钢丝绳与悬挂机构悬臂梁的等效刚度（N/m）。

代入相关参数可得额定载荷工况下的冲击载荷为P_额冲=1042.7N，额定载荷偏置工况下的冲击载荷为P_偏冲≈1175N。

由上面两种方法计算出的冲击应力P_max及对应的动载系数φ₁，结果对比见表3-4。

表3-4 动力学计算结果对比

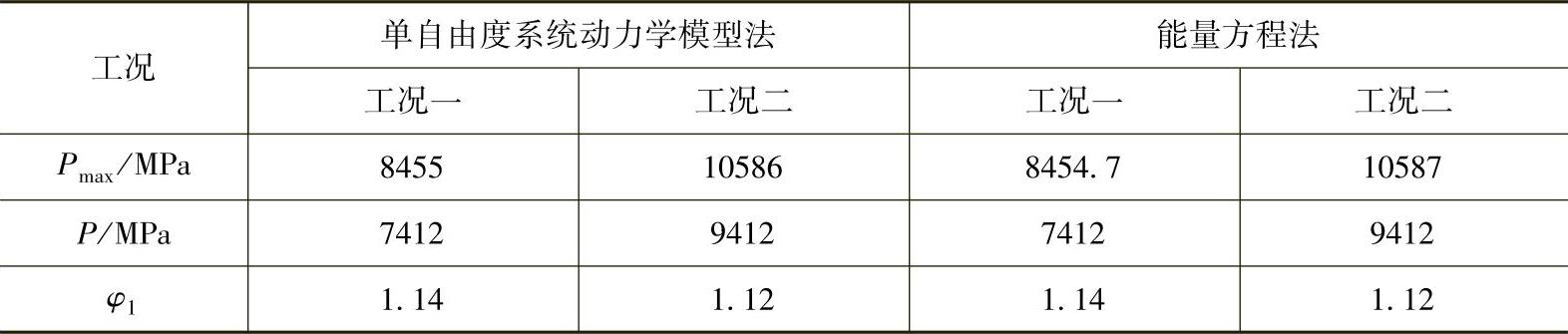
表3-4计算所得的动载系数值在1.12～1.14范围内，平均值为1.13。通过对施工平台起升系统建立动力学简化模型，将比较复杂的多自由度系统振动问题简化为单自由度力学模型进行分析计算，得出了悬吊平台突然离地起升时所引起的冲击载荷的大小，即由惯性载荷与振动载荷组成的附加冲击载荷，并获得了相应工况的动载系数。该方法作为一种较为简单粗略的分析方法，存在着一定的误差，误差主要来源于最初对多自由度系统的简化处理，以及计算过程中的计算误差。力学模型方法只能用于表示最初对问题的分析过程，想要获得较为精确的数据需要借助有限元分析的方法，对结构进行有限元建模，模拟实际工况进行瞬态动力学分析，得到较为精确的数据。

1.施工平台结构振动工况分析

施工平台在实际工作时，作业高度经常发生变化，随之带来的就是提升机的频繁起动和制动，各个机构都会产生一定的动力载荷，整机结构都要受到不同程度的冲击和振动影响。本节主要对高空作业施工装备中平台在以下几种可能出现瞬态冲击的特殊工况进行分析：

1）悬吊平台突然满载荷离地起升。

2）突然向悬吊平台内施加载荷。

3）悬吊平台受移动载荷作用。

其中，悬吊平台突然满载荷离地起升所引起的冲击振动是动力分析的关键所在。因为悬吊平台与地面接触时，起升钢丝绳通常处于松弛状态，这时如果突然开动提升机将承载的悬吊平台提升至空中并达到稳定速度，会产生较大的动态冲击。因此首先针对第一种情况进行分析。

通过对悬吊平台的整个离地起升过程进行分析后，发现最初只有一部分质量参加了振动。为了保持每个阶段系统质量的恒定不变，在建立悬吊平台突然离地起升的整机动力学模型时，主要分为以下三个阶段进行系统的分析：

（1）空载阶段 最初悬吊平台处于地面上时，起动提升机将原来处于松弛状态的钢丝绳收紧，此时钢丝绳并未承受平台自身及重物所产生的外载，因此提升机处于空转状态。在钢丝绳刚刚被收紧的瞬间，开始受力时，这一阶段结束。可以认为此时起升机构已处于稳定运行状态，悬吊平台还处于静止不动状态，但悬吊平台已具有向上的初速度v₀，其中速度的大小取决于钢丝绳的松弛程度及起升机构起动时间的长短。

（2）预张紧阶段 钢丝绳开始受载的瞬间即为此阶段的时间零点，直到悬挂机构悬吊点处的张力等于悬吊平台重力时为止。这一阶段，悬吊平台以前一阶段结束时的速度v₀向上运动，钢丝绳继续受力开始产生弹性变形，施工平台各部分结构产生振动，而悬吊平台仍在地面上，并未产生离地运动。该阶段结束的条件是当系统运动时间达到某一时间点t_l时，也就是钢丝绳受力恰好等于起升载荷时。

（3）起升阶段 上一阶段中悬吊平台已具有速度v₀，当平台以此速度离地上升时，即为此阶段时间零点，整机系统均处于自由振动状态。此时各部分结构已具有初位移和初速度。随着时间的增加，平台继续上升，起升瞬间对结构冲击产生的系统振动也开始逐渐衰减，最终稳定运行。

2.悬吊平台突然离地起升动力响应分析

悬挂机构前伸段属于悬臂梁结构，主要依靠张紧钢丝绳提供的预张紧力来抵抗外载荷的作用。悬吊平台在地面突然起升、空中突然卸载及空中起动或制动时，产生一定的动态冲击载荷，特别是当起升钢丝绳位于松弛状态下，提升机以全速提升满载的悬吊平台离地时，动载荷冲击比较大，也是设计悬吊平台时需要考虑的主要载荷工况之一。起升载荷通过钢丝绳传递形成对悬挂机构的冲击，并以集中力的形式施加到悬挂机构前端。为了方便计算和研究，本节选取了悬挂机构前端悬吊点作为研究对象，利用ANSYS分析了悬吊平台突然离地起升的瞬态动力响应，研究了该位置处位移随时间的变化情况，并对起升动载系数、动力响应稳态值进行了分析研究^[21]。

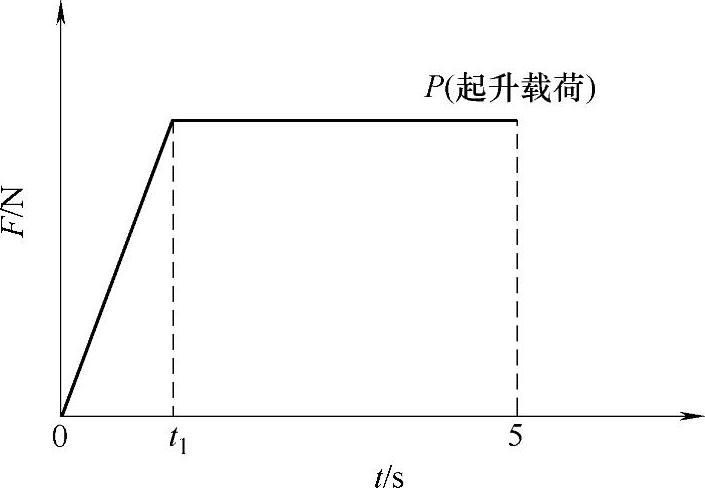
图3-26 起升过程中载荷变化曲线

（1）起升过程中载荷变化曲线 利用ANSYS进行瞬态动力学分析，起升过程中载荷变化曲线如图3-26所示。

从图3-26中可以看出，用有限元法分析悬吊平台突然离地起升过程的动力响应时，实际上预张紧阶段非常短暂。在这极短的时间内，整个结构会产生一个初始变形，变形程度的大小取决于该阶段时间的长短，时间越短，也就意味着冲击效应越大。各部件在开始动作前预先产生的变形也就越大，很明显这对机器的结构稳定性、可靠性等都具有一定的影响。所以，应该尽量延长预张紧阶段的作用时间（起升时间）t₁，才能保证整机性能稳定可靠。研究表明，该时间主要与起升速度以及起升重量有关。合适的起升时间应根据起升速度而定，由于GB19155—2003中并未给出关于起升时间的规定，通过查阅相关文献，参考起重机相关规范中对起升时间的计算方法，得到施工平台起升载荷的冲击时间在0.2～0.4s内，本文设定起升载荷冲击时间t₁=0.25s。由于悬挂机构悬臂梁前端悬吊点承受了整个平台包括起升重物及钢丝绳等的重量，故它的动力学特性具有一定的代表性。为了便于求解分析，选取该点作为研究对象，研究其受到起升载荷瞬态冲击后位移随时间的变化情况；同时找出瞬态冲击作用下结构的主要应力集中点，即结构的危险区域，动力学求解所获得的数据可以作为设计的有效依据。(www.daowen.com)

（2）悬挂机构瞬态动力学求解分析 以额定载荷均布、125%额定载荷和额定载荷偏置作为工况。因为瞬态动力学主要研究悬吊平台离地起升时刻结构的动力响应，故暂不考虑风载荷等水平载荷的作用，只按照承受竖直方向起升载荷来求解计算。利用ANSYS的瞬态动力学模块对悬挂机构起升冲击载荷进行瞬态动力学求解。将三种工况的瞬态动力学分析结果在时间历程后处理器中进行处理，得到了悬挂机构悬臂梁前端竖直（Y向）方向的位移、速度及加速度响应曲线，图3-27～图3-35所示分别为三种工况的位移、速度、加速度响应曲线。

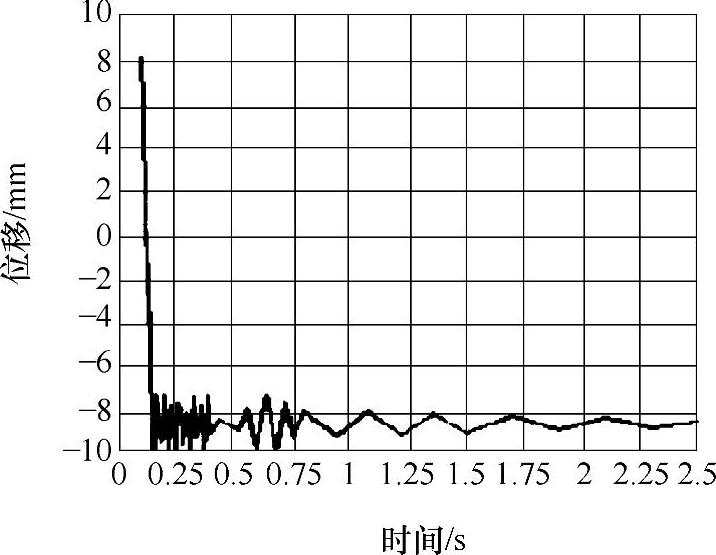
图3-27 额定载荷前端吊点Y向位移响应曲线

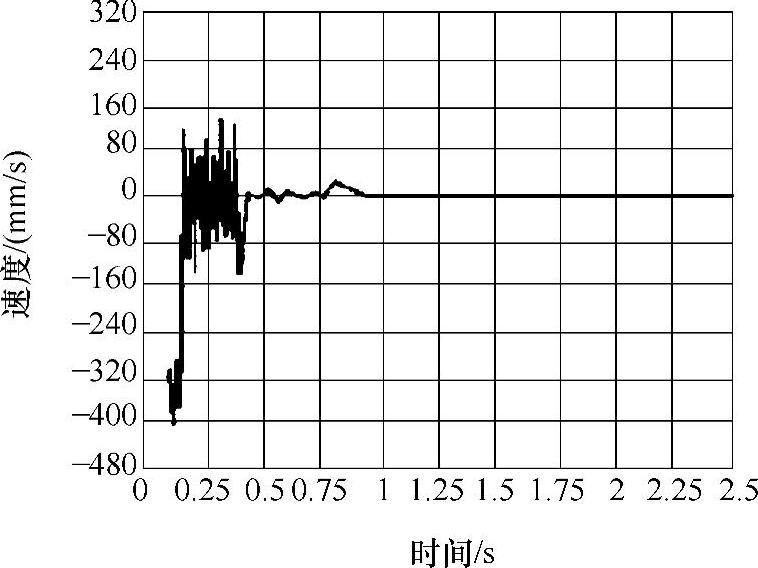
图3-28 额定载荷前端吊点Y向速度响应曲线

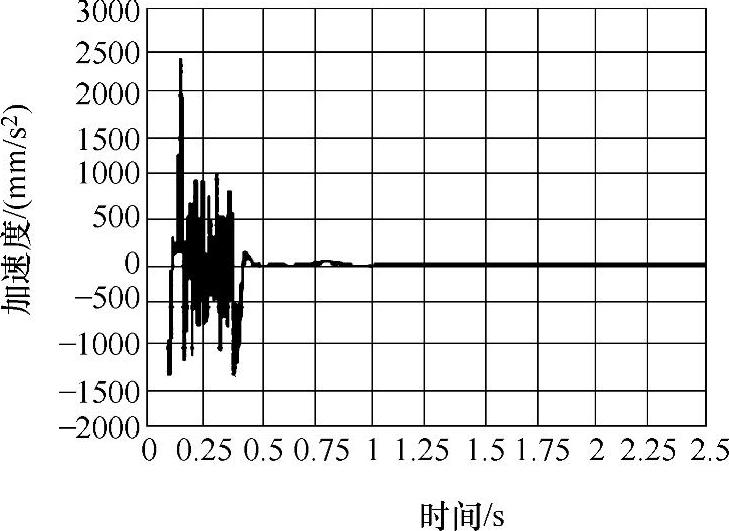
图3-29 额定载荷前端吊点 Y向加速度响应曲线

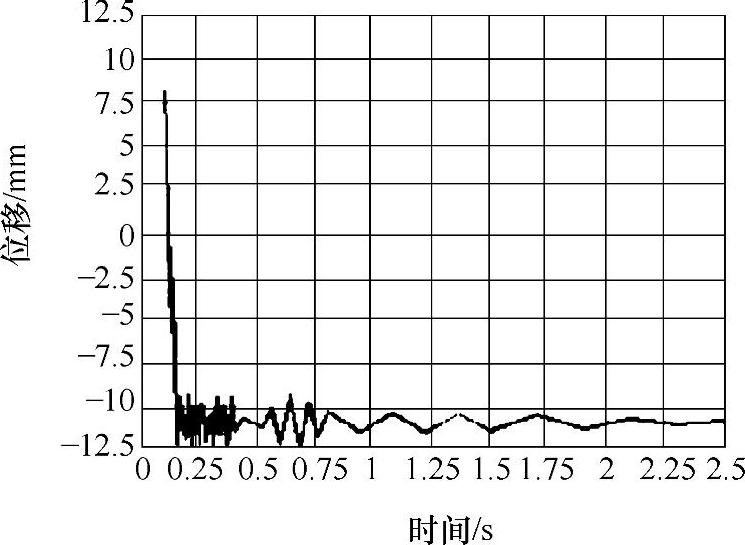
图3-30 125%额定载荷前端吊点Y向位移响应曲线

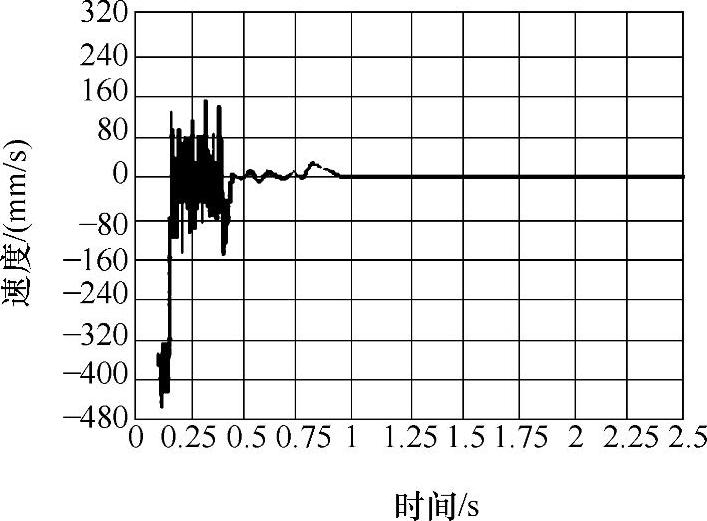
图3-31 125%额定载荷前端吊点Y向速度响应曲线

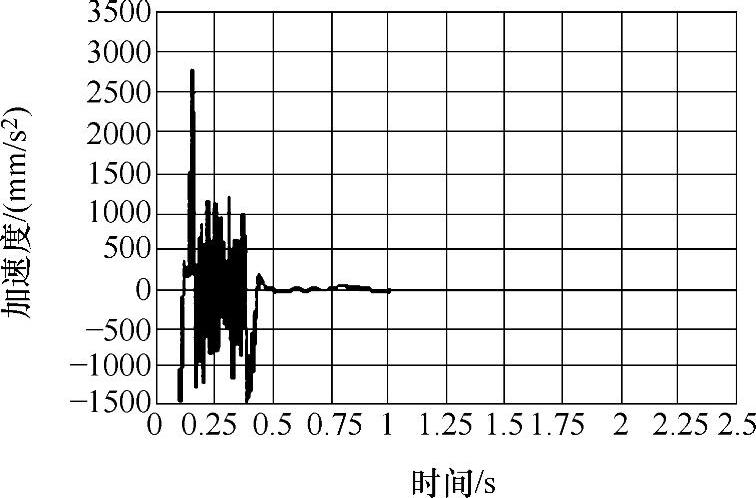
图3-32 125%额定载荷前端吊点Y向加速度响应曲线

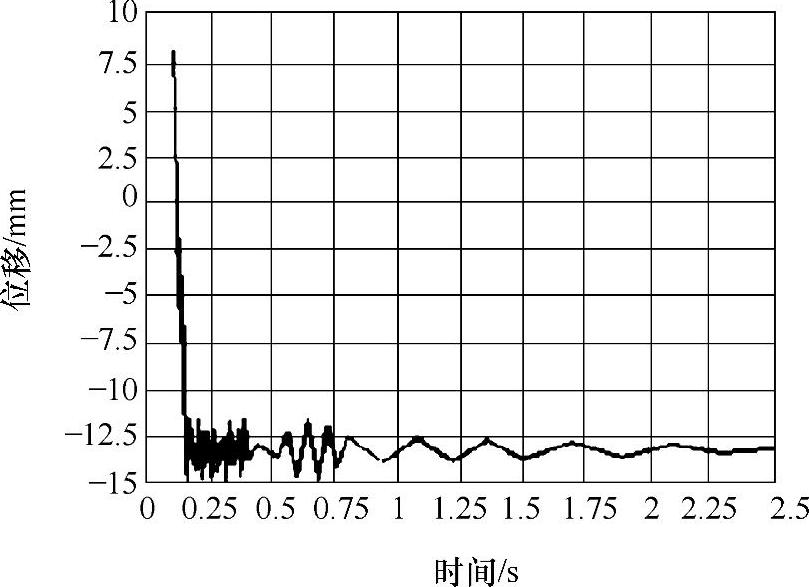
图3-33 额定载荷偏置前端吊点Y向位移响应曲线

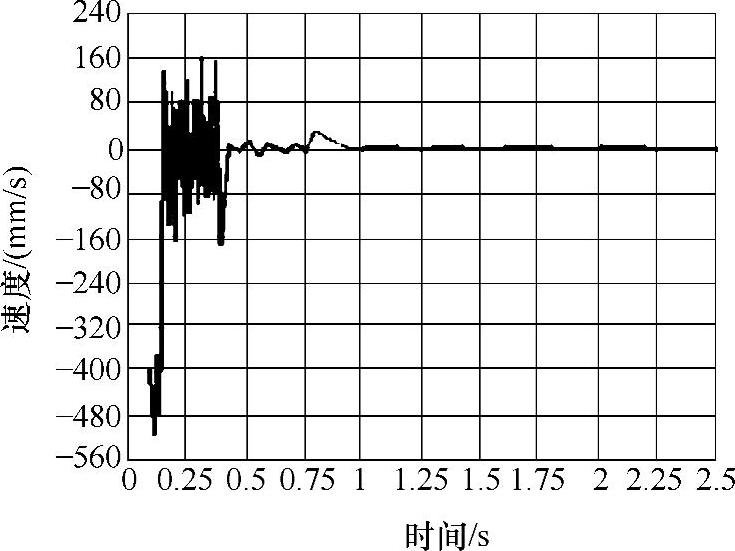
图3-34 额定载荷偏置前端吊点Y向速度响应曲线

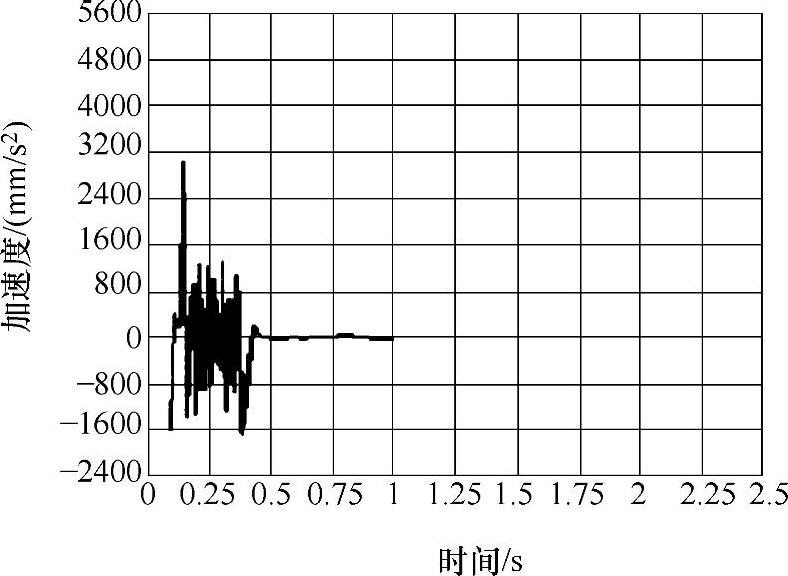
图3-35 额定载荷偏置前端悬吊点Y向加速度响应曲线

从瞬态动力学求解得出的动力响应曲线中可得出以下结论：

1）通过ANSYS瞬态动力学分析对施工平台三种载荷工况下离地起升时的瞬态冲击进行了仿真，获得的曲线可以较真实的反映出起升系统的结构动力学特性，可以很直观的看出悬吊平台突然离地起升对悬挂机构的冲击作用，可以更好的让设计操作人员了解设备的工作情况。

2）由位移响应曲线看出，随着时间的变化，系统的振动逐渐减弱，直至达到稳定值，额定载荷下悬臂梁吊点处位移达到的稳态值为-8.562mm，静力学分析得到的最大位移值为-8.631mm，两数值基本相同。三种工况的瞬态求解稳态值与静力分析值比较见表3-5。同时位移曲线的趋势与起升冲击载荷的趋势也基本一致。说明建模可靠，分析方法较为科学可行。

3）由三种工况的速度、加速度响应曲线可以看出，起升系统在1s内都处于冲击振动状态，特别是在0.5s内冲击振动较为强烈，随着时间的增加，系统逐渐由瞬态响应转化为稳态响应。实际施工中特别是当悬吊平台满载起升时，控制起升速度可以有效地降低对结构的冲击。目前变频技术广泛应用于工程起重机械，如果能采用变频技术对施工平台提升机构进行改进，实现在起动、制动情况下对速度的控制，这在一定程度上可以降低结构的疲劳损伤，达到延长结构寿命的目的。

表3-5 瞬态动力学求解稳态值与静力分析值比较

3.悬吊平台突然加载的动力响应分析

悬吊平台在实际施工过程中，常会出现在空中加载的情况。如果重物由一定高度落入悬吊平台内，这一过程重物会对悬吊平台产生很大的冲击动载荷，该载荷由提升机传到钢丝绳，再传到悬挂机构。这一系列反应在一定条件下会对各部件结构造成破坏，如钢丝绳被拉断，悬挂机构变形、倾翻等。因此，对这种工况下的动力响应进行计算是十分必要的。

由能量守恒定律可知，重物落入悬吊平台的过程中，减少的动能T和势能V应等于悬吊平台内增加的变形能U_d，即

T+V=U_d （3-22）

重物下落的起始速度及终止速度均为零，故动能T=0，悬吊平台底部达到最大位移δ_d时，重物减少的势能为

V=p（h+δ_d） （3-23）

式中 p——平台移动部分重量（N）；

h——平台下落高度（m）。

悬吊平台增加的变形能

式中 p_d——平台发生变形部分重量（N）；

δ_j——平台等效变形分量（m）。

如果考虑悬吊平台的质量，则有

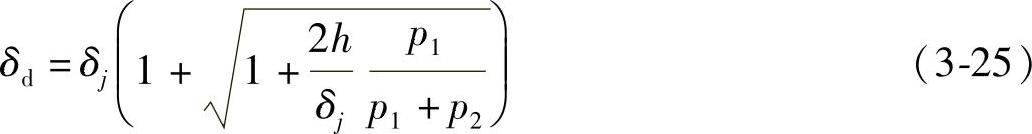
式中 p₁——重物的重量（N）；

p₂——悬吊平台的重量（N），悬吊平台空载自重为6370N。

由胡克定律知

可得冲击载荷

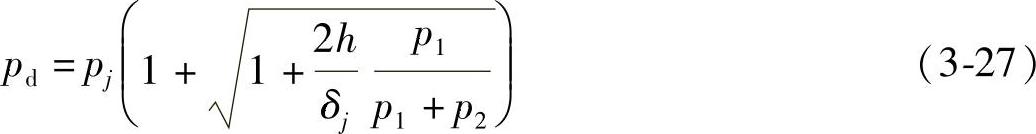
当加载不同质量的重物时，由式（3-27）可以计算出重物在不同高度下落时对悬吊平台的冲击载荷，见表3-6。

表3-6 重物在不同高度下落时对悬吊平台的冲击载荷

在整机结构有限元求解分析中，以ZLP800型高空作业施工装备的平台为研究对象，将向悬吊平台内加载重物过程分为两种情况：1）缓慢放入重物，2）突然放入重物。第一种情况下，重物无落差的缓慢放入悬吊平台中，该情况可以认为重物对悬吊平台无冲击载荷，按静力学进行分析即可。第二种情况，突然放入重物，物体在距平台底板一定高度的位置作自由落体运动，当下落到底板时，会对底板产生一定冲击载荷，应该按照瞬态动力学方法进行分析。运用ANSYS对上述两种情况下结构的位移、应力进行求解分析，其结果见表3-7。

表3-7 缓慢加载时的静力学求解结果

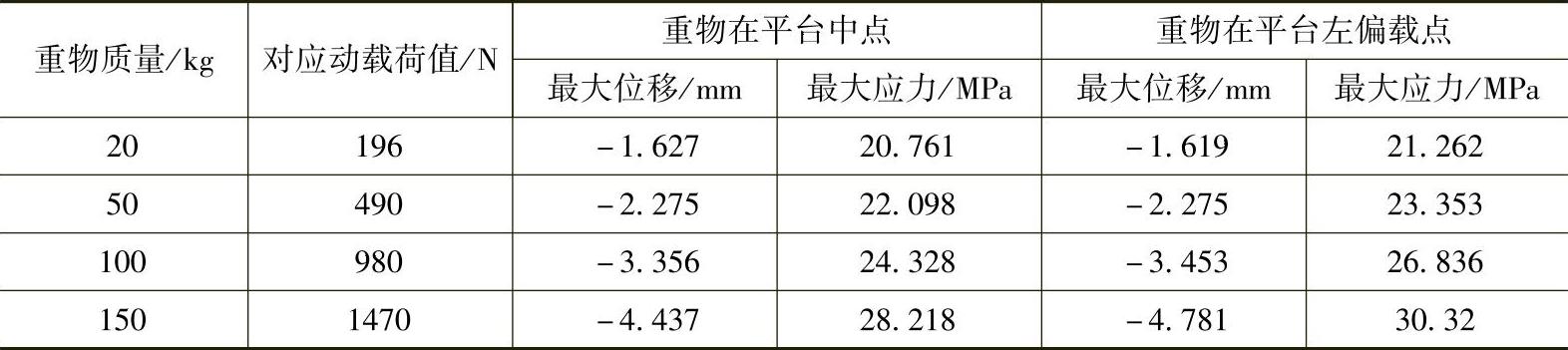
通过对整机结构的静力学及瞬态动力学求解分析可知，突然加载冲击过程中，结构中受载较大的区域主要集中在重物下落点、悬挂机构的悬吊点以及悬臂根部位置。鉴于此，提取了上述几个位置节点的位移、动应力响应曲线，如图3-36、图3-37所示。

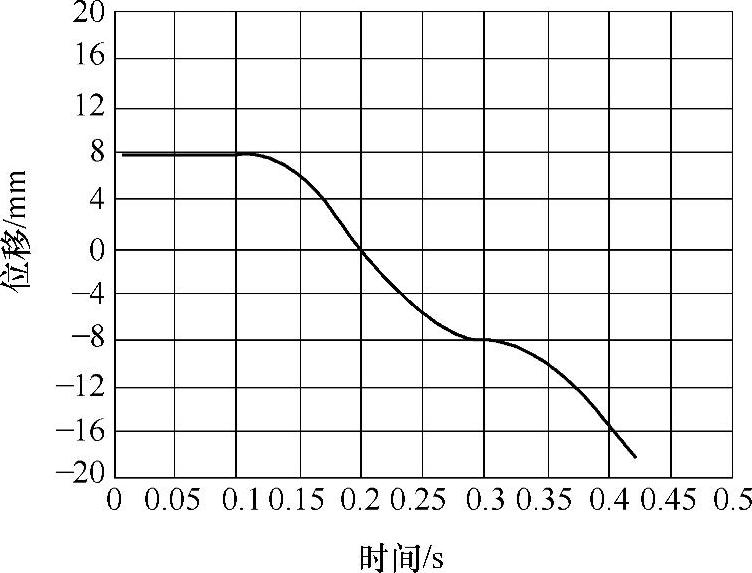
图3-36 150kg重物加载于中点的位移响应曲线

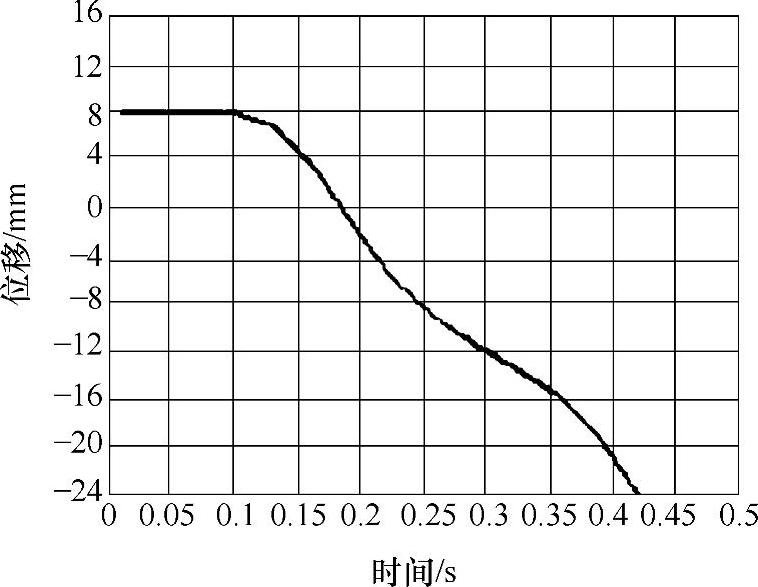
图3-37 150kg重物加载于左侧偏载点的位移响应曲线

图3-36、图3-37所示为在0.5m高度，突然向悬吊平台中点及左侧偏载点施加150kg重物时的位移响应曲线。随着时间的变化，加载点的位移逐渐增大，图3-37中的最大位移值已达到24.06mm。而GB19155—2003中规定悬吊平台最大变形量不能超过整体长度的1/300，即25mm。因此在施工中应尽量避免较重物体在具有一定高度差的位置落入悬吊平台中，否则会对结构造成破坏。

4.移动载荷作用下结构动力响应分析

悬吊平台在工作过程中，常会受到移动载荷的作用，移动载荷即载荷大小和作用方向都保持不变，作用位置却不断变化的荷载。如操作人员行走、材料机具等的搬运，都会对平台产生移动载荷的作用，其对整机结构的影响目前未见相关研究。而移动载荷作用下结构的瞬态响应分析具有广泛的工程应用前景，桥梁上承受火车、汽车和走动的人群等，厂房中的吊车梁承受的吊车荷载等都是移动载荷。

模型简化与方案构建：当移动物的质量与梁的质量相比较小时，可以忽略移动质量的惯性作用，将其简化为移动载荷作用下梁的动态响应分析问题。对匀速移动载荷问题，构建冲击等效加载方案，简化力学模型如图3-38所示。将其等效为多个点冲击载荷，施加在ZLP800型高空作业吊篮有限元模型上进行整机动态响应分析。

根据施工现场的环境，在悬吊平台上移动应相对较慢，以v=0.5m/s作为载荷移动速度进行分析，整个悬吊平台的长度L=7.5m，并考虑移动物体质量变化的影响，对此工况进行瞬态动力学求解，求解结果见表3-8。

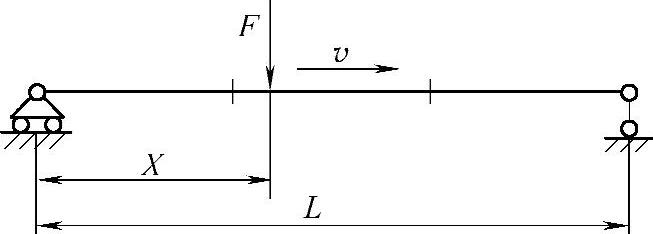
图3-38 移动载荷作用下悬吊平台简化力学模型

表3-8 多种移动载荷作用下结构瞬态求解结果

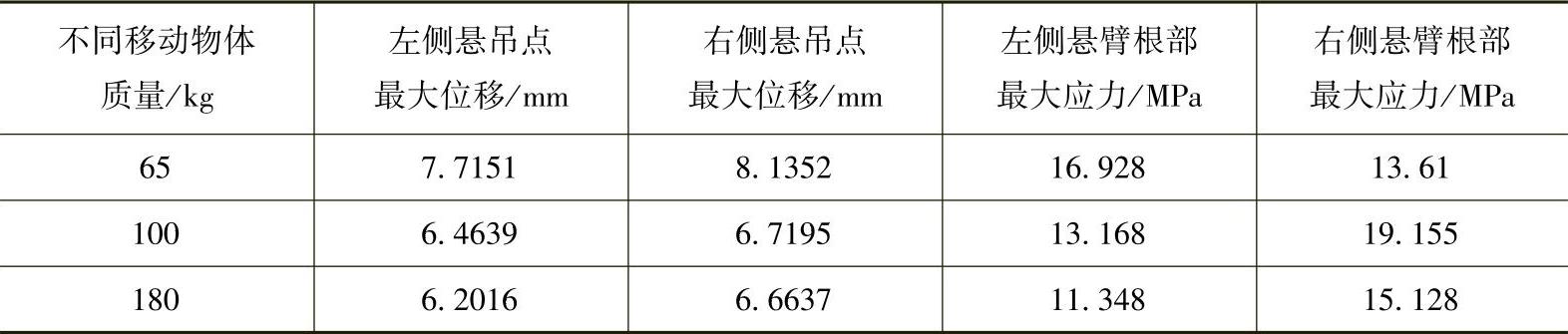
由分析结果可以看出：不同质量的物体在平台内以0.5m/s的速度移动时，两悬挂机构的位移、应力变化较小，其值均在允许范围内，不会对结构造成破坏性影响。由此可说明，以较小速度在平台内移动时对结构影响可以不予考虑。通过提高移动速度后，再进行上述计算，悬挂机构上的最大位移、应力值有所增大。同时，移动的物体对底板有沿速度反方向的摩擦力作用，速度越快，摩擦力越大，对平台产生一定大小的水平力，会使悬吊平台产生摆动，这又对悬挂机构产生了横向载荷作用。通过计算获得，当物体在平台内移动速度不超过2m/s时，可以保证整机的结构安全，运行稳定。