图论广泛应用在信息科学、社会科学以及生态学的食物链与食物网分析，是量化网络连接度和流量的重要方法。根据Harary 的分类，图是由一系列的节点和连接它们的线段所组成的。图论中的路径是不同的节点连接线段所组成的。路径的长度是由对于线段的特殊定义而决定的。路径分为闭合的环形路径和不闭合的分枝路径。

在景观生态学的相关研究中，图论极大地推动了与连接度和生态流相关研究的发展。在生态连接度的研究中，通过对图中要素参数赋予特定的生态意义，图能较好地反映结构连接度和功能连接度，以一种直观和可视化的方式表示区域和自然系统的网络特性，为跨尺度分析以及景观动态的直接表示提供框架。

网络理论是图论(graph theory)的主要内容，其核心是用简单的图形来直观反映现实世界中复杂的结构关系。目前，网络理论已广泛应用于众多领域，如在计算机科学和运筹学领域中解决网络中最高效的网络、线路或流的确定问题，在生态学中分析食物网连接度和能量流的问题，近年来，这一理论在生物多样性保护规划与管理中也开始受到重视。网络理论可用网络结构模型来表达，网络由一系列具有空间拓扑结构的节点(node)和边(edge)组成，其中节点表示网络中的个体要素，边表示节点之间的连接关系。节点不仅反映个体要素在网络结构中的位置，而且可以通过一定的权重反映其质量、大小、重要性等属性，根据网络所反映信息是否带有权重，可将网络分为权重网络(weighted networks)和非权重网络(non-weighted networks)。边的长度可反映节点之间联系的紧密程度，也可带有方向性，因此，根据边有无方向性可将网络分为有向网络(directed networks)和无向网络(un-directed networks)。

根据网络的拓扑结构特征，可将其分为平面网络、随机网络、无标度网络和小世界网络等类型，其中无标度网络和小世界网络为复杂网络。

无标度网络一般由少数具有较高连接数的节点和多数具有低连接度的节点相互连接构成。它对随机干扰具有较高的恢复能力，但对关键点的干扰会导致整个网络分裂。小世界网络中的大部分节点彼此不邻接，但它们之间存在经由少数节点的捷径，因此具有较小的路径长度和较高的聚集度。(www.daowen.com)

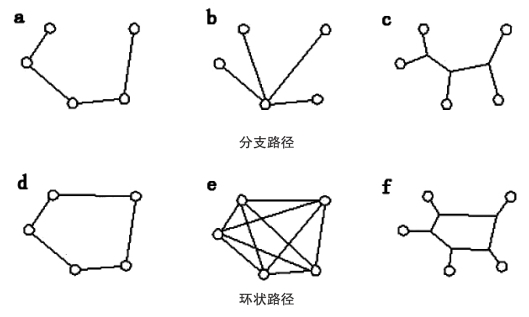
图4-5 图论中典型的路径结构

图论可以直观地反映城市生态网络的结构关系，并反应生态过程中“源”、“汇”、“踏脚石”的生态概念及其生态功能。