相比于非线性模型预测控制（NMPC），线性时变模型预测控制（LTV MPC）具有计算量小，易求解等特点。本节将介绍如何将非线性系统转换为线性时变系统。

当前时刻系统状态量和控制量分别为ξ0∈χ，μ0∈Ω。对系统式（7－4）施加控制量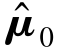（k）＝μ0，k≥0，当前系统状态量参考值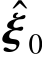（k）＝ξ0，k≥0。

式（7－16）即为线性时变系统（LTV），其描述了非线性系统式（7－4）的状态量ξ（t）与状态量参考值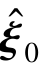（t）之间的偏差关系。

式（7－16）可写成如下形式：

式（7－16）与式（7－17）是等价的，都是系统式（7－4）在工作点处近似线性化所得到的线性时变系统。

为进一步降低模型预测控制算法的计算复杂度，做如下假设：

1.预测模型设计

首先考虑以下非线性动力学系统：

式中：f（·，·）为系统的状态转移函数，ξ（t）∈ℝn为n维状态变量，μ（t）∈ℝm为m维控制变量，η（t）∈ℝp为p维输出变量。

将非线性系统式（7－19）转化为如下的离散的线性时变系统：

下面根据离散的线性时变系统式（7－20）设计模型预测控制器。将式（7－20）中的控制输入由控制量μ（t）转变为控制增量Δμ（t），将式（7－20）表示的系统状态方程中的输入矩阵、输出矩阵和传递矩阵等做相应的变换，即可得到如式（7－22）所示新的状态空间表达式。

首先做如下设定：

式中：0m×n是m×n维0矩阵，0m是m维列矩阵，Im是m维单位矩阵。

得到新的状态空间表达式如下：

若已知t时刻系统的状态量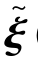（t）和控制增量Δμ（t），通过式（7－22），即可预测t＋1时刻系统的输出量η（t＋1），不断迭代，即可得到k时刻的系统输出量η（k｜t）。

新的状态空间方程的系统输出量可计算如下：

2.QP问题转化(www.daowen.com)

系统控制时域Hc内的控制增量ΔU（t）是未知的，通过设定合理的优化目标函数并使其最小化，可求得在控制时域Hc内满足约束条件的最优控制序列。

考虑目标函数如下：

其中，第一项用于惩罚系统在预测时域Hp内，输出量与参考输出量之间的偏差，即反映了系统对参考轨迹的快速跟踪能力，第二项用于惩罚系统在控制时域Hc内的控制增量大小，即反映了系统对控制量平稳变化的要求，第三项用于惩罚系统在控制时域Hc内的控制量大小，即反映了系统对控制量能量消耗尽可能小的要求。然而由于系统是实时变化的，在控制周期内不能保证每个时刻满足约束条件的优化目标函数都能求得最优解。因此有必要在优化目标函数中加入松弛因子，保证在控制周期内无最优解的情况下，系统以求得的次优解代替最优解，防止出现无可行解的情况发生。

以上形式的优化目标函数是一般形式，为便于计算机编程求解，可通过适当处理转换为标准二次型，即二次规划（Quadratic Programming，QP）问题。

将式（7－38）代入式（7－39）中，经过相应的矩阵计算，即可得到标准二次型目标函数。具体计算过程如下：

首先做如下设定：

于是，在满足控制约束的条件下，在每一个采样周期内使目标函数J（ξ（t），μ（t－1），ΔU（t），ε）优化问题等价于如下的二次规划问题：

式中：

Ycmin（t）和Ycmax（t）分别为硬约束输出量的下限和上限，Yscmin（t）和Yscmax（t）分别为软约束输出量的下限和上限，Ξ＝ε1pu，其中1pu为pu维列向量且所有元素都为1。

式（7－51）为控制增量约束条件，式（7－52）限制了控制量极限值，式（7－53）为硬约束输出量约束条件，式（7－54）为软约束输出量条件。

式（7－50）最优问题是一个二次规划问题，在满足线性约束条件（7－51）～（7－55）的情况下，求解最优控制量ΔU（t），使目标函数（7－50）最小化。

式（7－50）二次规划问题可以写成以下标准形式：

若已知t时刻的状态量ξ（t）和前一时刻的控制量μ（t－1），在控制周期内通过对式（7－56）～式（7－58）最优化求解，可得到在控制时域Hc内的最优控制增量序列。

在控制时域Hc内的最优控制增量系列定义如下：

将该最优控制增量系列的第一个作为实际的控制增量作用于系统，即