考虑如下的离散非线性系统：

其中：f（·，·）为离散非线性系统的状态转移函数，ξ（t）∈ℝn为n维状态变量，μ（t）∈ℝm为m维控制输入变量，η（t）∈ℝp为p维输出变量，χ∈ℝn为状态量集合，Ω∈ℝm为控制输入量集合。

假设系统的原点为f（0，0）＝0，以该点为系统的控制目标。对于任意N∈Z＋，考虑如下代价函数：

式中：JN（·，·）：ℝn×ℝNm→ℝ＋，U（t）＝[μ（t），…，μ（t＋N－1）]为N时域范围内的控制输入序列，ξ（k）（k＝t，…，t＋N）是式（7－4）在控制输入序列U（t）作用下所得到的轨迹状态量系列。

每一步长所求解的有限时域的优化问题如下：(www.daowen.com)

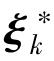式（7－8）和式（7－9）分别为状态量和控制量的约束，式（7－10）为初始状态量，式（7－11）为状态量终端约束。通过求解式（7－6）表示的优化问题，可得到t时刻的最优控制量序列，系统式（7－7）在最优控制量序列U*t的作用下，即可得到最优状态量序列（k＝t，…，t＋N）。

一般将控制量序列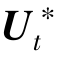的首个元素作为实际控制输入作用于系统式（7－7）。在下一采样周期内，系统以新的采样时刻作为初始状态求解优化问题式（7－6）～式（7－11），继续将最优控制量序列的首个元素作为实际控制输入作用于系统式（7－7）。如此反复，以滚动优化的形式完成上述优化问题。在方程求解过程中，其包含了N×（m＋n）个最优变量和N×n个非线性状态约束，以及由控制量约束和状态量约束所组成的线性约束。因此，对于非线性模型预测控制，其求解的复杂程度与系统状态方程的阶数有关，其求解难度随着系统阶数的增加而迅速增加。对于阶数较高的非线性系统，如多自由度车辆动力学模型，若不进行适当的简化，非线性模型预测控制算法很难在线实时求解。

非线性模型和复杂的非线性约束增加了非线性模型预测控制问题求解难度。本章所研究的智能车辆控制问题是基于车辆多自由度非线性动力学模型，要求在线实时控制。而非线性模型预测控制算法很难保证在线实时控制，并不适用于求解多自由度非线性系统问题。

若将非线性系统线性化，采用线性模型预测控制算法进行求解，则其计算量将会大大减小。线性化系统根据其是否随时间而变化的特点，可分为线性时不变系统（Linear Time Invariant，LTI）和线性时变系统（Linear Time Variant，LTV）。研究表明，线性时不变系统在高速下的控制误差较大，无法获得满意的控制效果。若实时在当前工作点附近对系统线性化，即将其转化为线性时变系统（LTV），则相比于直接求解非线性问题，可显著减小计算量，同时相比于线性时不变系统（LTI），可较大提高控制精度。