对于负障碍检测，需要将负障碍和非负障碍样本点看作属于两种类别，可以把问题看作二分类问题。在介绍logistic回归、SVM和随机森林三种可解决二分类问题的机器学习算法之前，先对利用机器学习算法求解时会面临的一些共性问题进行介绍。

1.机器学习共性问题

1）机器学习模型的超参数优化方法

机器学习中的超参数优化旨在寻找使得机器学习算法在验证数据集上表现性能最佳的超参数。所谓超参数，与一般的模型参数不同，是定义模型属性或者定义训练过程的参数，是在训练前提前设置的。举例来说，随机森林算法中决策树的数量就是一个超参数，而神经网络中的权值则不是超参数。超参数优化需要找到一组超参数，这些超参数返回一个优化模型，该模型减少了预先定义的损失函数，进而提高了给定数据集的预测精度。

超参数优化方法有手动调参和自动化寻优方法。手动调参依赖大量的经验，并且比较耗时，因此发展出了许多自动化超参数优化方法。自动化寻优包括网格化寻优（Grid Search）方法、随机寻优（Random Search）方法、贝叶斯优化方法（Bayesian Optimization）、基于梯度的优化方法（Gradient－based Optimization）、进化寻优（Evolutionary Optimization）等方法。其中网格化寻优可以说是最基本的自动化超参数优化方法，使用这种技术，只需为所有超参数的可能取值构建独立的模型，评估每个模型的性能，并选择产生最佳结果的模型和超参数。

2）过拟合与正则化

当机器学习模型把训练模型学得“太好”时，很可能已经把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质，这样就会导致泛化性能下降，这种现象在机器学习中称为“过拟合”（overfitting）。与“过拟合”相对的是“欠拟合”（underfitting），这是指对训练样本的一般性质尚未学好。通常希望的是模型处于过拟合与欠拟合中间的状态。

为防止过拟合，有两种办法比较通用，一种是使用更多的数据作为训练集，但实际情况并不总能获得大量的数据；另外一种就是正则化方法。正则化方法是在总损失函数中添加含有模型参数的正则化项。采用这种正则化方法能削弱不重要的特征变量，从许多的特征变量中“提取”重要的特征变量，减小模型参数的数量级。

正则化项可以取不同的形式，例如，回归问题中，损失函数是平方损失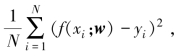下面为其添加正则化项。正则化项可以是参数向量w的L2范数，如式（2－3）的总损失函数中的这一项：

3）精确度、准确率、召回率、F1分数介绍

精确度、准确率、召回率、F1分数是机器学习算法的重要评价指标，下面分别对其概念进行介绍。

假设原始样本中有两类，其中：类别1为所关心的类别，总共有P个类别为1的样本，也称作正例样本或正样本；另外还有N个类别为0的样本，也称作负例样本或负样本。

经过机器学习分类器分类后，有TP个类别为1的样本被系统正确判定为类别1，FN个类别为1的样本被系统误判定为类别0，显然有P＝TP＋FN；有FP个类别为0的样本被系统误判定为类别1，TN个类别为0的样本被系统正确判定为类别0，显然有N＝FP＋TN。

那么：

精确度（Precision）：Precision＝TP/（TP＋FP），反映了被分类器判定的正例中真正的正例样本的比例；

准确率（Accuracy）：Accuracy＝（TP＋TN）/（P＋N）＝（TP＋TN）/（TP＋FN＋F P＋TN），反映了分类器对整个数据样本集合的判定能力——能将正样本判定为正，负样本判定为负；

召回率（Recall），也称为True Positive Rate：Recall＝TP/（TP＋FN），反映了被正确判定的正例占总的正例的比例；

F1分数（F1－score）：分类问题的一个衡量指标，一些多分类问题的机器学习中，常常将F1－score作为最终测评的方法，它是精确率和召回率的调和平均数，最大为1，最小为0，计算公式如式（2－5）所示：

4）交叉验证法

交叉验证法（cross validation）是一种评估模型性能的重要方法，主要用于在多个模型中（不同种类模型或同一种类不同超参数组合）挑选出在当前问题场景下表现最优的模型。常见交叉验证的方法为：先将数据集D划分为k个大小相似的互斥子集，每个子集都尽可能保持数据分布的一致性，即从数据集D中分层采样得到。然后每次用k－1个子集的并集作为训练集，余下的那个子集作为测试集，这样就可获得k组训练/测试集，从而可进行k次训练和测试，最终返回的是这k个测试结果的均值。显然，交叉验证法评估结果的稳定性在很大程度上取决于k的取值，为强调这一点，通常把交叉验证法称为“k折交叉验证”（kfold cross validation）。(www.daowen.com)

2.三种机器学习算法简介

1）logistic回归简介

logistic回归是一种利用回归函数来进行分类的方法，利用sigmoid函数h（z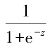）＝（其中z＝θ0＋θ1 x1＋θ2 x2＋…＋θn xn＝θT x，x为样本特征向量）对样本进行拟合，sigmoid函数的输出值在0～1区间，可将其作为二分类的类别预测概率值。

对于logistic回归算法的训练，h（z）可变换为式（2－6）：

它表示了样本属于式（2－7）、式（2－8）两个类别的概率：

对于单个样本，构造损失函数如式（2－9）所示：

即总损失函数（不包含正则项）如式（2－10）所示：

logistic回归模型的训练过程就是利用训练样本找出能使Lθ取极小值的θ。

2）SVM简介

SVM（Support Vector Machine，支持向量机）原理是找出样本中的最大分类间隔，而落在最大间隔处的样本就叫作支持向量（Support Vector）。

假设样本集（xi，yi），i＝1，2，…，n，对于正样本yi＝1，对于负样本yi＝－1，在线性情况下分类线方程为wx＋b＝0，则它需要满足式（2－11）：

即把两类样本点分别保持在分类线两边函数距离大于1处，并且还需要使得分类间隔最大。

利用Lagrange方法引入Lagrange乘子αi，i＝1，2，…，n，把上述问题化为如式（2－12）、式（2－13）所示的最优化问题：

在非线性情况下，可以用径向基核函数、多项式核函数等代替原来的线性分类方程，在SVM中这类函数叫作核函数。

由于SVM函数能找出最大分类间隔这一特性，其在分类问题中的精度、泛化能力比较好。由于样本可能存在噪声，导致无法找出完美的分类间隔，因此也常常在上述优化问题中引入一项分类损失项，并用惩罚系数C控制它在优化目标中的占比大小，从而通过调整C的大小允许存在比如对于部分噪声样本的分类错误。

3）随机森林简介

随机森林是包含多个决策树的分类器，决策树是一种常用的机器学习方法。它利用样本的各个特征来构造一棵树，树的非叶子节点代表了决策条件，叶子节点则代表了分类结果。因此，沿着根节点依据决策条件对样本进行决策以选择接下来的枝干一直到叶子节点，就完成了分类过程。

决策树的构造依据信息论中的一些准则，优先选择那些对样本类别影响最大的特征来构建决策树，但是决策树构建得太深则容易过拟合。随机森林就是一种综合了多个决策树的分类结果来降低过拟合提高精度的方法。它采用有放回的采样技术来从样本集中每次提取部分样本构造决策树，并且在选择特征构造决策树时会选择特征的随机子集。