1.反弯点法的适用范围

反弯点法适用于各层结构比较均匀（各层层高变化不大，梁的线刚度变化不大），节点梁柱线刚度比∑ib/∑ic＞3的多层框架（i为梁、柱的线刚度）。

2.反弯点基本假定

（1）确定层间各柱的剪力时，假定梁的线刚度与柱的线刚度之比为无限大，即略去梁本身的变形；认为同层各柱上下两端均不发生角位移。

（2）确定层间各柱的反弯点位置时，认为除底层以外的其余各层柱，受力后上下两端的转角相同；即假定除底层柱的反弯点位于离柱底2/3的底层层高处外，其余各层柱的反弯点均位于该层层高中间部位。

（3）由于不考虑框架梁的轴向变形，则框架节点只有水平侧移，且同层各柱的侧移均相同。

3.反弯点法的求解步骤

在水平荷载作用下，不能再用分层法分析框架内力，这是因为分层法的两个基本假定已不再适用。多层多跨框架在风荷载或其他水平荷载作用下，其荷载一般都可简化为节点水平集中力的作用，其弯矩图如图3.8所示。各杆的弯矩图都是直线，每个立柱一般都有一个反弯点。当然，各柱的反弯点位置未必相同。图3.8为该框架受力后的变形图，各柱的上、下端既有水平位移，又有角位移（即柱端转角）。(www.daowen.com)

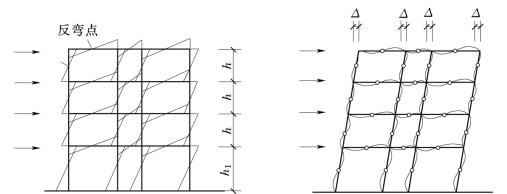
图3.8　框架在水平荷载作用下的弯矩和变形示意图

如果框架不考虑轴力所引起的各杆变形，则在同一横梁标高处，各柱端都将产生一个相同的水平位移，同一层各柱上下端的水平位移差Δ也相等。如果梁的线刚度比柱的线刚度大得多（例ib/ic＞3），上述的节点角位移就很小。

如果能求出各柱的剪力及其反弯点的位置，则柱和梁的弯矩都可求得，所以对在水平荷载作用下的框架近似计算，一是需确定各柱间的剪力分配比，二是需确定各柱的反弯点位置。

以所示多层框架为例，将框架沿顶层各柱的反弯点处切开以示出剪力与轴力，按水平方向的平衡条件及柱的侧移刚度求解各柱剪力。即由假定（1）可得柱端水平剪力大小，根据假定（2）可知，除底层外的各层柱，其反弯点位于该柱的高度中央，底层柱的反弯点则位于离柱底2/3的底层层高处。

有了各柱的剪力，确定了反弯点位置后，顶层各柱的弯矩图就可绘出。根据假定（3），利用节点垂距平衡，顶层各梁的弯矩图也可求得，同理可求出其他各层的弯矩图。如求第三层各柱的剪力时，只需取第三层柱的反弯点以上部分作为隔离体接以上方法求解即可。其他各层柱与梁的弯矩图也可绘出。