双向板按塑性理论计算的方法很多，塑性绞线法是最常用的方法之一。塑性绞线与塑性绞的概念是相仿的，塑性绞出现在杆系结构中，而板式结构则形成塑性绞线，两者都是因受拉钢筋屈服所致。

一般将裂缝出现在板底的称为正塑性绞线；裂缝出现在板面的称为负塑性绞线。用塑性绞线法计算双向板分两个步骤：首先假定板的破坏机构，即由一些塑性绞线把板分割成由若干个刚性板所构成的破坏机构；然后利用虚功原理，建立外荷载与作用在塑性绞线上的弯矩之间的关系，从而求出各塑性绞线上的弯矩，以此作为各截面的弯矩设计值进行配筋设计。

从理论上讲，塑性绞线法得到的是板的一个上限解，即板的承载力应小于等于该解。实际上由于穹隆作用等有利因素，试验结果得到的板的破坏荷载都超过按塑性绞线法算得的值。

1.塑性绞线法的基本假定

（1）沿塑性绞线单位长度上的弯矩为常数，等于相应板配筋的极限弯矩。

（2）形成破坏机构时，整块板由若干个刚性节板和若干条塑性绞线组成，忽略各刚性板块的弹性变形和塑性绞线上的剪切变形及扭转变形，即整块板仅考虑塑性绞线上的弯曲转动变形。

2.破坏机构的确定

由前述可知，均布荷载作用下的四边简支双向板，沿短方向跨中板带的跨中正弯矩最大，该处板底将首先出现裂缝，随着荷载不断增大，裂缝沿长跨方向延伸发展，在接近短边时分叉沿对角线方向向四角发展，荷载继续增大，短跨跨中的受拉钢筋应力将首先达到屈服，但此时板并不会立即破坏，荷载还可以继续增加，与裂缝相交的钢筋应力也依次达到屈服，最终形成与裂缝图形类似的塑性绞线，将板分成四个板块，成为破坏机构，板达到其极限承载力。

图1.31　均布荷载下四边固定双向板的塑性绞线

对于均布荷载作用下的四边连续（四边固定）双向板，短方向跨中板带的支座处负弯矩最大，其次是长方向跨中板带的支座负弯矩及短方向跨中板带的跨中正弯矩。因此，裂缝首先在板面沿长边的支座处出现，其次是板面沿短边的支座处及板底短跨跨中出现裂缝，继续加载，板底短跨跨中裂缝沿平行于长边方向延伸，接近短边时分叉向四个板角延伸，荷载继续增加，板中钢筋应力按裂缝出现的顺序依次达到屈服，形成如图1.31所示的塑性绞线，将板分成四个板块，成为破坏机构，板达到其极限承载力。对负弯矩引起的塑性绞线称为“负塑性绞线”，图1.31中用波形虚线表示。

有时破坏机构不止一个，这时需要研究各种破坏机构，求出最小的承载力。当不同的破坏机构可以用若干变量来描述时，可通过承载力对变量求导数的方法得到最小承载力。

3.基本原理

根据虚功原理，外力所做的虚功应该等于内力所做的虚功。设任一条塑性绞线的长度为l，单位长度塑性绞线承受的弯矩为m，塑性绞线的转角为θ。

由于除塑性绞线上的塑性转动变形外，其余变形均略去不计，因而内功U等于各条塑性绞线上的弯矩向量与转角向量相乘的总和，即：

式中　∑——对各条塑性绞线求和。

外力所做的功W等于微元ds上的外力大小与该处竖向位移乘积的积分，设板内各点的竖向位移为w、各点的荷载集度为p，则外功为：

对于均布荷载，各点的荷载集度相同，p可以提到积分号的外面，而是板发生位移后倒角锥体体积，用V表示，可利用几何关系求得。于是式（1.22）可写成：

虚功方程可表示为：

从式（1.24）可以得到极限荷载与弯矩的关系。

楼盖中最常见的是四边支承矩形板。现在来分析四边固定矩形双向板的极限承载力。根据前面介绍的判别塑性绞线位置的方法，可以确定板的破坏机构，如图1.32所示。共有五条正塑性绞线（因四条斜向塑性绞线相同均用1表示，水平塑性绞线用2表示）和四条负塑性绞线（分别用3、4、5、6表示）。这些塑性绞线将板划分为四个板块。短跨（l01）方向，跨中极限承载力用M1u表示，两支座的极限承载力分别用M＇1u和M″1u表示；长跨（l02）方向，跨中极限承载力用M2u表示，两支座的极限承载力分别用M＇2u和M″2u表示。

图1.32　四边固支板的破坏机构

单位长正塑性绞线的受弯承载力：

单位长负塑性绞线的受弯承载力：

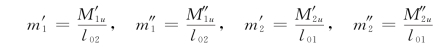
为了简化，近似取斜向塑性绞线与板边的夹角为45°。设点e和点f发生单位竖向位移，则各条塑性绞线的转角分量及绞线在x、y方向的投影长度为：

塑性绞线1（共四条）：

θ1x＝θ1y＝，l1x＝l1y＝

塑性绞线2：(www.daowen.com)

θ2x＝， θ2y＝0； l2x＝l02－l01， l2y＝0

塑性绞线3、4：

θ3x＝θ4x＝，θ3y＝θ4y＝0； l3x＝l4x＝l02， l3y＝l4y＝0

塑性绞线5、6：

θ5x＝θ6x＝0， θ5y＝θ6y＝； l5x＝l6x＝0， l5y＝l6y＝l01

于是，内功为：

可求得外功：

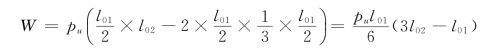
最后由虚功方程，得到：

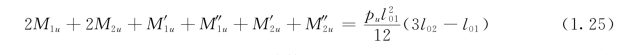
式（1.25）就是连续双向板按塑性绞线法计算的基本公式，它表示了双向板塑性绞线上正截面受弯承载力的总值与极限荷载pu之间的关系。

4.设计公式

双向板设计时，把上述极限均布荷载pu用均布荷载设计值p代替；各截面总的受弯承载力用相应的弯矩设计值代替。但一个方程无法同时确定多个变量，因此需要补充附加条件。

令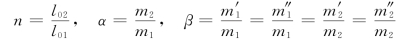

于是，正截面受弯承载力的总值可以用n、α、β和m1，来表示：

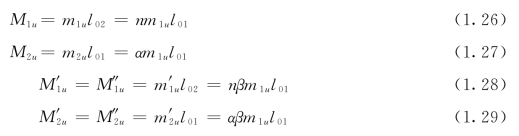
代入式（1.25），即得：

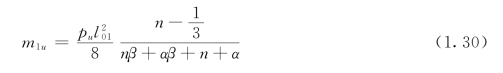
设计双向板时，令荷载设计值p＝pu，长短跨比值n为已知，这时只要选定α和β值，即可按式（1.30）求得m1u，再根据选定的α与β值，求出其余的正截面受弯承载力设计值m2u、m＇1u、m＇2u。考虑到应尽量使按塑性绞线法得出的两个方向跨中正弯矩的比值与弹性理论得出的比值相接近，以期在使用阶段两个方向的截面应力较接近，宜取；同时考虑到节省钢材及配筋方便，根据经验，宜取β＝1.5～2.5，通常取β＝2.0。

为了合理利用钢筋，参考弹性理论的内力分析结果，通常将两个方向的跨中正弯矩钢筋在距支座l01/4处弯起50%，弯起钢筋可以承担部分支座负弯矩。这样在距支座l0/4以内的正塑性绞线上单位板宽的极限弯矩值分别为m1/2和m2/2，故此时两个方向的跨中总弯矩分别为：

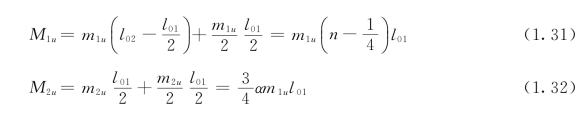
支座上负弯矩钢筋仍各自沿全长布置，亦即各负塑性绞线上的总弯矩值没有变化。将式（1.32）代入式（1.25），即得：

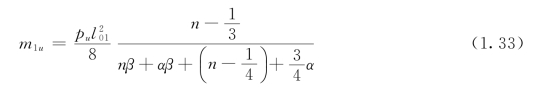
式（1.33）就是四边连续双向板在距支座l01/4处将跨中钢筋弯起一半时短跨方向每米正截面承载力设计值m1u的计算公式。

对于具有简支边的连续双向板，只需将下列不同情况下的支座弯矩和跨中弯矩代入式（1.25），即可得到相应的设计公式。

（1）三边连续、一长边简支。此时简支边的支座弯矩等于零，其余支座弯矩和长跨跨中弯矩不变，仍按式（1.28）、式（1.29）和式（1.32）计算，而短跨因简支边不需要弯起部分跨中钢筋，故跨中弯矩为：

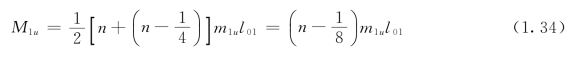
（2）三边连续、一短边简支。此时简支边的支座弯矩等于零，其余点座弯矩和短跨跨中弯矩不变，仍按式（1.28）、式（1.29）和式（1.31）计算，长跨跨中正截面受弯承载力设计值为：

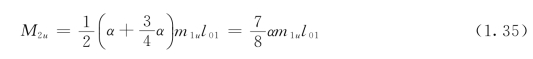
（3）两相邻边连续，另两相邻边简支。此时的两个方向的跨中弯矩分别取（1）和（2）两种情况的弯矩值。

当部分跨中钢筋弯起后，弯起处正弯矩的承载力下降，所以有可能在该处先于跨度中央出现塑性绞线，形成如图1.33所示的向下幂式破坏机构。此时可以按图示破坏机构进行承载力复核。

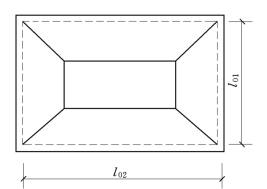
图1.33　双向板向下的幂式破坏机构