1.弯矩调幅法的概念和原则

在广泛的试验研究基础上，国内外学者曾先后提出过多种超静定混凝土结构考虑塑性内力重分布的计算方法，如极限平衡法、塑性绞法、变刚度法、强迫转动法、弯矩调幅法以及非线性全过程分析方法等。但是上述方法大多数计算繁冗，离工程设计应用尚有距离，目前，只有弯矩调幅法为多数国家的设计规范所采用。我国颁布的《钢筋混凝土连续梁和框架梁考虑内力重分布设计规程》（CECS51：93）也推荐用弯矩调幅法来计算钢筋混凝土连续梁、板和框架的内力。

弯矩调幅法是考虑塑性内力重分布确定连续梁、板设计弯矩的一种实用计算方法，其基本概念是对结构按弹性理论所算得的弯矩值和剪力值进行适当调整，以考虑结构非弹性变形所引起的塑性内力重分布。通常的做法是对支座弯矩进行调整，然后按调整后的内力进行截面设计和配筋构造。

截面弯矩的调整幅度用弯矩调幅系数β来表示，即：

式中　Me——按弹性理论算得的弯矩值；

Ma——调幅后的弯矩值。

图1.13为一两跨的等跨连续梁，在跨度中点作用有集中荷载F。按弹性理论计算，支座弯矩Me＝－0.188Fl0，跨度中点的弯矩M1＝0.156Fl0。现将支座弯矩调整为Ma＝－0.15Fl0，则支座弯矩调幅系数，此时，跨度中点的弯矩可根据静力平衡条件确定。设M0为按简支梁确定的跨度中点弯矩，，由图1.13，可求得：

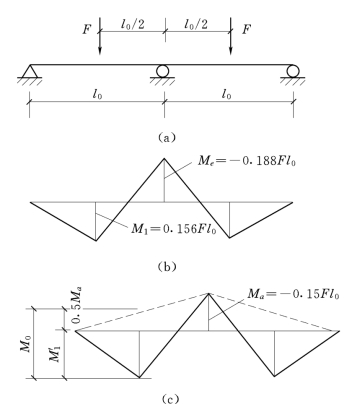
图1.13　弯矩调幅法中力的平衡

（a）计算简图；（b）按弹性理论计算弯矩图；（c）支座弯矩调幅后的弯矩图

可见经过调幅后的支座负弯矩降低了，而跨中正弯矩增大了。

综合考虑塑性内力重分布的影响因素以后，我国的《钢筋混凝土连续梁和框架梁考虑内力重分布设计规程》（CECS51：93）和《混凝土结构设计规范》（GB50010—2002）提出了下列设计原则：

（1）按考虑塑性内力重分布的分析方法设计的结构和构件，尚应满足正常使用极限状态的要求或采取有效的构造措施。

（2）受力钢筋宜采用HPB235，HRB335，HRB400级热轧钢筋，混凝土强度等级宜在C20～C45范围内，截面的相对受压区高度ξ应满足0.10≤ξ≤0.35。

弯矩调幅法按下列步骤进行：

（1）用（线）弹性理论方法计算，并确定荷载最不利布置下的结构控制截面的弯矩最大值Me。

（2）采用调幅系数β降低各支座截面的弯矩设计值，即：

式中，β值不宜超过0.2。

（3）结构的跨中截面弯矩值应取弹性理论分析所得的最不利弯矩值和按下式计算值中的较大值：

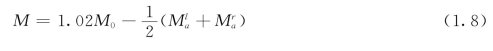
式中　M0——按简支梁计算的跨中弯矩设计值；

、——连续梁或连续单向板的左、右支座截面弯矩调幅后的设计值。

（4）调幅后，支座和跨中截面的弯矩值均不应小于。

（5）各控制截面的剪力设计值按荷载最不利布置和调幅后的支座弯矩由静力平衡条件计算确定。

2.用调幅法计算等跨连续梁、板

（1）等跨连续梁。

承受相等均布荷载时，各跨跨中和支座截面的弯矩设计值：

承受间距相同、大小相等的集中荷载时，各跨跨中和支座截面的弯矩设计值：

承受相等均布荷载时，支座边缘的剪力设计值：

承受间距相同、大小相等的集中荷载时，支座边缘的剪力设计值：

式中　g、q——沿梁单位长度上的恒荷载设计值、活荷载设计值；

G、Q——梁上一个集中恒荷载设计值、活荷载设计值；

αm——考虑塑性内力重分布的弯矩计算系数，按表1.1采用；η——集中荷载修正系数，按表1.2采用；(www.daowen.com)

αv——考虑塑性内力重分布梁的剪力计算系数，按表1.3采用；

l0——梁的计算跨度，按表1.4采用；

ln——梁的净跨度；

n——跨内集中荷载的个数。

表1.1　连续梁和连续单向板考虑塑性内力重分布的弯矩计算系数αm

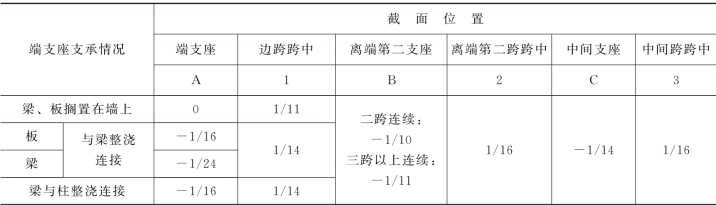
注　1.表中系数适用于荷载比q/g＞0.3的等跨连续梁和连续单向板。
2.连续梁或连续单向板的各跨长度不等，但相邻两跨的长跨与短跨之比值小于1.10时，仍可采用表中弯矩系数值。计算支座弯矩时应取相邻两跨中的较长跨度值，计算跨中弯矩时应取本跨长度。

表1.2　集中荷载修正系数η

表1.3　连续梁考虑塑性内力重分布的剪力计算系数αv

表1.4　梁、板的计算跨度l0

注　表中b—梁的支承宽度；a—板的搁置长度；h—板厚。

（2）等跨连续单向板。

承受相等均布荷载时，各跨跨中和支座截面的弯矩设计值：

式中　g、q——沿板跨单位长度上的恒荷载设计值、活荷载设计值；

αm——连续单向板考虑塑性内力重分布的弯矩计算系数，按表1.1采用；

l0——板的计算跨度，按表1.4采用。

3.用调幅法计算不等跨连续梁、板

相邻两跨的长跨与短跨之比小于1.10的不等跨连续梁、板，在均布荷载或间距相同、大小相等的集中荷载作用下，各跨跨中及支座截面的弯矩设计值和剪力设计值仍可按上述等跨连续梁、板的规定确定。对于不满足上述条件的不等跨连续梁、板或各跨荷载值相差较大的等跨连续梁、板，现行规程提出了简化方法，可分别按下列步骤进行计算。

（1）不等跨连续梁。

1）按荷载的最不利布置，用弹性理论分别求出连续梁各控制截面的弯矩最大值Me。

2）在弹性弯矩的基础上，降低各支座截面的弯矩，其调幅系数β不宜超过0.2；在进行正截面受弯承载力计算时，连续梁各支座截面的弯矩设计值可按下列公式计算。

当连续梁搁置在墙上时：

当连续梁两端与梁或柱整体连接时：

式中　V0——按简支梁计算的支座剪力设计值；

b——支座宽度。

3）连续梁各跨中截面的弯矩不宜调整，其弯矩设计值取考虑荷载最不利布置并按弹性理论求得的最不利弯矩值和按式（1.8）算得的弯矩值的较大值。

4）连续梁各控制截面的剪力设计值，可按荷载最不利布置，根据调整后的支座弯矩用静力平衡条件计算，也可近似取考虑活荷载最不利布置按弹性理论算得的剪力值。

（2）不等跨连续板。

1）从较大跨度板开始，在下列范围内选定跨中的弯矩设计值：

边跨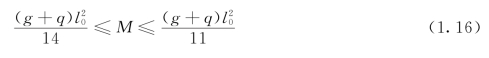　

中间跨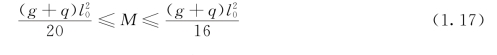　

2）按照所选定的跨中弯矩设计值，由静力平衡条件，来确定较大跨度的两端支座弯矩设计值，再以此支座弯矩设计值为已知值，重复上述条件和步骤确定邻跨的跨中弯矩和相邻支座的弯矩设计值。