从结构上讲，TIN是一种典型的矢量数据结构。它主要通过节点（地形采样点）、三角形边和三角形面之间的关系来显式或隐式地表达地形散点的拓扑关系，因此设计一个高效、结构紧凑、维护方便的TIN的存储与组织结构对TIN的应用与库的维护是至关重要的。

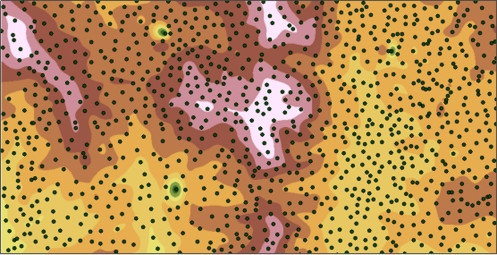
图10-7　多项式插值效果图

TIN的基本单元三角形的几何形状直接决定着TIN应用质量。由于地形的自相关性，相互接近的地形采样点之间的关联程度愈大。理论与实践均证明：狭长的三角形其插值精度比较规则的三角形插值精度可信度要低。因此，在TIN中，三角形的几何形状有着严格的要求。一般的有三条原则：①尽量接近正三角形；②保证最近的点形成三角形；③三角形网络唯一。此为三角剖分的原则问题（曹鸿博，2010）。

一个良好的数据结构和三角剖分准则，必须由一个高效的算法和程序实现。算法在具体应用中发挥的作用由算法本身的性能和实现它的程序质量共同决定。而程序的好坏很大程度上依赖于算法的原理。对算法本身在理论上进行分析论证，寻求一种高效率、高精度、适用面广的算法是TIN建立中重要一环。

由上述的分析可知，TIN的数据组织、三角剖分准则、算法和程序构成了TIN的基本理论体系框架，图10-8表示了这一结构。

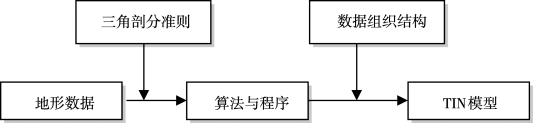
图10-8　TIN模型构建流程(www.daowen.com)

1.三角剖分准则及算法分类

TIN的三角剖分准则是指TIN中三角形的形成法则，它决定着三角形的几何形状和TIN的质量。目前在GIS、计算几何和计算机图形学领域常用的三角剖分准则有以下几种（刘学军、符锌砂，2001）：空外接圆准则、最大最小角准则、最短距离和准则、张角最大准则、面积比准则、对角线准则。

通常将在空外接圆准则、最大最小角准则下进行三角剖分称为Delaunay三角剖分，简称为DT（Delaunay Triangulation），同时空外接圆和最大最小角也是Delaunay三角网的两个基本性质。DT三角剖分是目前应用最为广泛的三角剖分方法，其特性是可最大限度地避免狭长三角形的出现以及不管从何处开始构网都能保持三角形网络的唯一性。

TIN的三角剖分就是按照Delaunay三角剖分，将地形采样点用互不相交的直线段连接起来，并按一定的结构进行存储。到目前为止，已出现了不少成熟的三角化算法。并且随着时间的推移，老算法不断地得到完善，也会出现更好的算法。因此准确地对算法进行归类是比较困难的。这里按照地形采样数据的分布情况对TIN的三角化算法进行归类，DTM采样数据一般分为呈不规则分布、规则分布和等高线数据分布三类。针对不规则分布数据，TIN三角化算法主要有DT三角剖分、辐射扫描法、退火模拟法、数学形态法；针对规则分布数据，TIN三角化算法主要有VIPs算法、循环迭代算法、层次三角形算法；针对等高线数据，TIN三角化算法主要有特征线算法、探测优化算法（汤国安等，2009）。由于等高线数据是通过原始采样点数据处理后得到的，而直接获取规则分布数据的情况不多，因此利用不规则分布采样数据构建TIN是构建地形模型的最常用方式。

2.不规则采样点三角剖分算法

散点域（不规则采样点）的三角剖分目前使用最为广泛的算法是Delaunay直接三角剖分算法。Tsai（1994）根据实现过程，把DT三角剖分分成分割合并算法、三角网增长算法和逐点插入算法三类（杨广义，2010）。

用来进行TIN构建的原始数据根据数据点之间的约束条件可分为无约束数据域和约束数据域两种类型。无约束数据域是指数据点之间不存在任何关系，即数据分布完全呈离散状态，数据点之间在物理上相互独立。而约束数据则是部分数据点之间存在着某种联系，这种联系一般通过线性特征来维护，如地形数据中的山脊线、山谷线上的点等。约束条件又有两类，一是边界约束条件，是指数据点被一多边形所包围，该多边形即为边界约束条件；另一为内部约束条件，是数据点之间存在的限制条件。地形数据一般仅存在内部约束条件而无边界约束。