1.规则格网（Grid）模型

规则格网模型将空间区域分成规则的等距离单元，每个单元对应一个数值，通常在数学上表示为一个矩阵，在计算机中表现为一个二维数组，每个格网单元或数组元素对应一个高程值，是地形表达的主要形式之一（图10-1）。

按平面上等间距规则采样，或内插所建立的数字地面模型，称为基于栅格的数字地面模型，可以写成以下形式：

式中，zi，j为栅格结点上的地面属性数据，包括土地权属、土壤类型、土地利用等。当该属性为海拔高程时，该模型即为数字高程模型；当该属性为海底深度时，该模型即为数字海底地形模型。

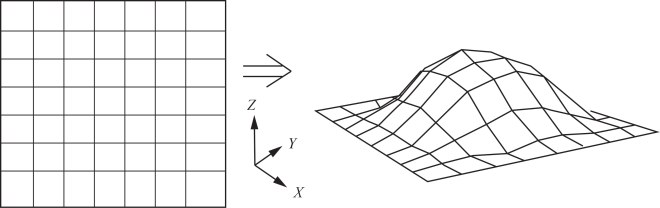
图10-1　规则格网模型

2.不规则三角网模型

由于受观测手段所限，在实际应用中获取的数据通常是不规则分布的离散点数据。如地震观测的地层结构数据、环境监测获取的地下水资源监测点数据、气象监测的点数据等。

不规则三角网模型（TIN）通过不规则分布的数据点，生成连续的三角形面来逼近地形表面（图10-2）。三角形的形状和大小取决于不规则分布的观测点数据的位置和分布密度。用来描述TIN的基本元素有三个：节点（Node）、边（Edge）和面（Face）。

图10-2　TIN模型

节点：是相邻三角形的公共顶点，也是用来构建TIN的采样数据。

边：指两个三角形的公共边界，是TIN不光滑性的具体反映。边同时还包含特征线、断裂线以及区域边界。

面：由最近的三个节点所组成的三角形面，是TIN描述地形表面的基本单元。TIN中的每一个三角形都描述了局部地形倾斜状态，具有唯一的坡度值。三角形在公共节点和边上是无缝的，或者说三角形不能交叉和重叠。

节点、边和面之间存在着关联、邻接等拓扑关系。

利用某区域所构建的TIN模型，可以很容易获取地面上任一点的高程或生成地形剖面。计算任一点高程时，分为任意点落在三角面的顶点、边上或三角形内三种情况。如果点不在顶点上，则该点的高程值通常通过线性插值得到。

3.等值线模型(www.daowen.com)

等值线是DEM模型的平面表示形式，是地形表示中广泛使用的一种表示方法。

等值线图以符号化的模型来表示三维地形形态，是由一系列数值相等的点连成曲线来反映连续递变的面状分布地形特征，如等高线、等深线、等温线等。

等值线是指平面上的轨迹分布线，如图10-3所示。等值线的值所表示的物理意义可以是地形高程或水下深度数据、温度场中的温度数据、气象中的气压数据等。

等值线符合以下要求：

①给定的等值线在相应区域内不能互相交错；

②一根等值线通常是一条连续的曲线；

③给定值后，相应域上等值线不限于一条；

④等值线可以是闭合曲线，也可以和域外连续。

图10-3　等值线模型

4.常用DTM数据模型比较

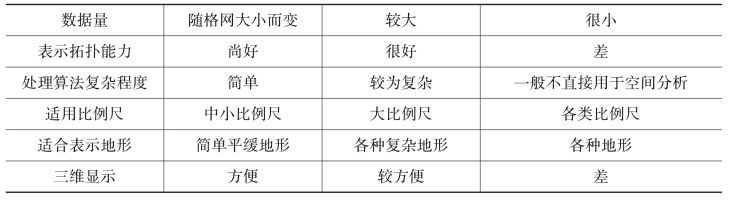
规则格网模型、TIN模型和等值线模型各有优缺点，各个模型对比如表10-1所示。

表10-1　常用DTM数据模型比较

续表