从测深原理可知，测深精度受多种因素的影响，其中吃水、上下升沉、水位、姿态等引起的在垂直方向上的变化经常交织在一起，很难截然分开，采用传统的测深模式分别进行改正，不可避免地会带来一定的误差，最终影响测深精度。如果能有一种手段，可以直接测定换能器的垂直综合动态效应，将明显改善最终测深精度。

近20年来，GNSS定位技术取得了长足的发展，近海动态定位已达厘米级，技术已相对成熟，远海采用后处理动态，甚至实时动态已可达到厘米级精度。船载GNSS天线得到的大地高变化，直接反映了换能器的垂直综合动态变化，GNSS高精度三维定位结果，为测深垂直综合动态效应改正提供了技术手段。需要注意的是，GNSS天线得到的是大地高，其与瞬时水深值及天线高相减，得到的是海底点的大地高。若是进行水下地形测量，须将大地高转换到地形要求的高程上来，一般为正常高，海洋中正高与正常高一致（似大地水准面与大地水准面重合），不用考虑正高与正常高的差别，因此须已知该测区GNSS椭球面与（似）大地水准面的偏差模型；若是图载水深测量，须已知测深点处深度基准面对应的大地高，即已知该测区GNSS椭球面与深度基准面的偏差模型。偏差模型可采用高程/深度拟合或采用多源数据建立精化模型的方式得到，如果测区范围较小，距离岸边较近，可近似将偏差值看作常数，在岸边采用GNSS水准联测的方式获取。

如图9-23所示，HZ为大地水准面至海底的距离，H0为GNSS天线至参考椭球面的垂直距离，即GNSS天线大地高；H1为平均海面至参考椭球面的垂直距离，即平均海面大地高；H2为换能器表面至海底的垂直距离，即测深仪记录的瞬时水深；H3为GNSS天线至换能器表面的垂直距离，在补偿各种姿态变化后可认为H3为常量；H4为海底至参考椭球面的垂直距离，即海底点的大地高；ξ为平均海面至大地水准面的垂直距离，即海面地形；N为大地水准面至参考椭球面的垂直距离，即大地水准面差距（或高程异常）；L为从平均海面起算的理论深度基准面的高度；h为深度基准面至海底点的垂直距离，即图载水深。

从图9-23中可知，以下关系式成立：

因此海底点的大地高为：

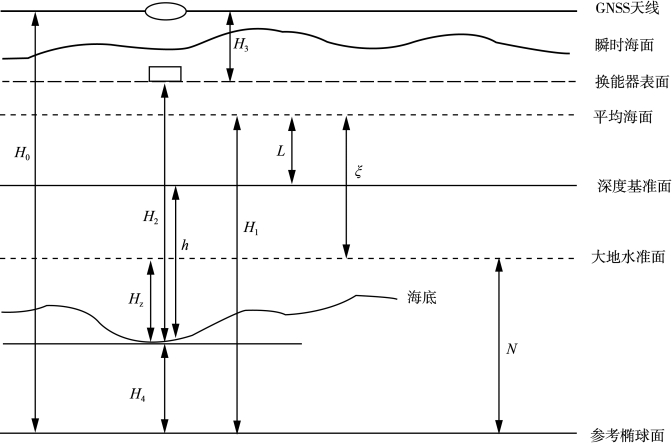
图9-23　基准面之间的转换关系

(www.daowen.com)

平均海面大地高为：

式中，h+H4为深度基准面大地高，因此

由大地水准面起算的海底点高程为：Hz＝N-H4，即

式（9.56）与式（9.57）即为由GNSS天线大地高推算其图载水深和正高的基本公式（许家琨，2011）。从式中可看出，无论成果采用正常高还是图载水深表达，此情形下垂直方向上测量成果都与潮汐、动态吃水、上下升沉无关。在瞬时水深测量中把这些因素作为一个整体因素进行考虑，这在很大程度上削弱了由于潮汐、动态吃水、涌浪等在垂直方向上引起的测量误差，明显提高了测量成果的精度；另外，该方法也减少了部分工作过程，比如验潮，节省了大量的人力与测量成本，这正是GNSS高精度动态测高模式进行水下地形测量的优势所在。只要能精确确定大地水准面差距N及平均海面的大地高H1，即可实现该区域GNSS大地高H0和海图成果水深h及海底地形高程之间的精密转换。