水位改正的实质是在瞬时测深值中去除海面潮汐时变影响，将测得的瞬时深度转化为一定基准上与时间无关的“稳态”深度场的数据处理过程（刘雁春，2003）。在实际工作中，根据需求选择不同的垂直基准面，如我国水下地形图通常采用1985国家高程基准，航海图采用理论最低潮面。由于在测量过程中，无法实现测区内所有测深点的潮汐观测，因此通常采用以点代面的水位改正方法，即根据潮汐变化规律，在测区内设置一定数目的验潮站，利用验潮站的实测水位变化来推算测区内某测点处的水位变化情况（暴景阳等，2006）。

在开展水下地形测量工作前，通常需要收集测区潮汐资料，了解潮汐性质，由此来对测区进行水位分区、分带。若无历史资料，也可根据海区自然地理（海底地貌、海岸形状等）条件，或布设临时验潮站短期验潮加以分析。水位分区、分带主要分为以下三种情况：

①测区范围较小且潮汐性质相同。这种情况下，通常认为测区各点处水位高度在同一平面，可在测区附近设立单一验潮站（测区水位高度位于同一水平面），并用该站的水位数据进行单站水位改正，或布设多个验潮站（测区水位高度位于同一直线或平面，但不是水平面）采用距离加权内插的方法进行水位改正。

②测区范围较大且潮汐性质相同，潮位高度不在同一平面。根据潮汐传播规律，可采用分带法、时差法或最小二乘法进行水位改正。

③测区范围内潮汐性质存在不同。如果测区范围较大，存在各处潮汐性质不同的现象。这种情况下，应将测区按潮汐性质划分为各个子区，使其潮汐性质相同，再根据情况采用内插法、分带法、时差法或最小二乘法，对各子区进行水位改正。

下面具体介绍验潮站的有效作用距离及常用的各种水位改正方法。

1.验潮站的有效作用距离

计算验潮站的有效作用距离，对合理布设验潮站以及决定水位改正模型，有着重要的意义。根据测区附近的已有两个验潮站的潮汐调和常数计算其间的瞬时最大潮高差，并按两个验潮站的距离计算测深精度相对应的距离，即为按测深精度要求的验潮站有效作用距离，公式可表达为：

式中，d为验潮站有效距离（km）；δz为测深精度（cm）；S为两站之间的距离（km）；Δhmax为两站在同一时间的最大可能潮高差（cm）。

利用式（9.33）估计有效距离，关键是求Δhmax，通常有三种方法（刘雁春，2003）：

①同步观测比对法：根据两站同步观测资料，绘出大潮期间几天的水位变化曲线（从平均海面起算），从图上找出Δhmax；

②解析计算法：利用两站的4个主要分潮构成的准调和潮高模型，计算出Δhmax；

③数值计算比对法：利用两站的11个分潮构成的调和潮高模型，计算两站一段时期的潮高值，选出Δhmax。

2.单站水位改正法（时间内插法）

当测区位于一个验潮站的有效范围内，可认为测区所有点水位变化与该站相同，因此可用该站的水位资料来进行水位改正，单站水位改正法是实际野外数据处理中最为常用的一种潮汐内插方法。垂直基准面以深度基准面为例，图9-13中，Z t（）表示观测时刻的水位改正值（从深度基准面起算的潮高），H表示瞬时水深观测值，则图载水深HD（从深度基准面起算的水深）为：

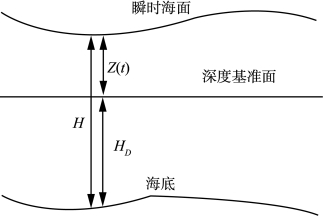
图9-13　单站水位改正原理图

验潮站水位观测数据为离散值，为了求得不同时刻的水位改正数，需要进行时间内插，一般采用解析法，早期采用图解法。图解法就是绘制水位曲线，以横坐标表示时间，纵坐标表示水位改正数，如图9-14所示，可求得任意时刻的水位改正数。解析法就是利用计算机以观测数据为采样点进行时间内插来求得测量时间段内任意时刻水位改正数的方法，常用的内插方法有线性内插、多项式插值、样条插值等。

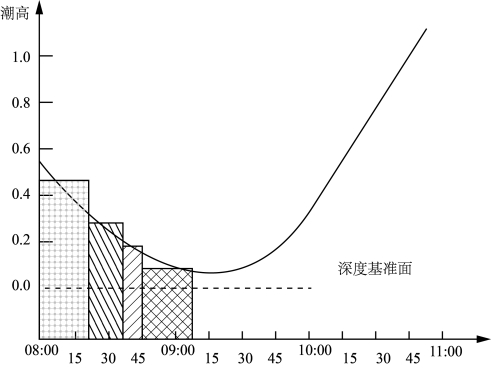
图9-14　单站水位改正图解法

3.距离加权内插法

测区范围不大，并假定测区内所有测点的水位处于同一直线或平面内，确定该直线或平面后，即可求得测点任意时刻的水位。距离加权内插法也是比较常用的一种水位改正方法。如图9-15所示，测区位于A、B两验潮站之间，任何测点的水位可根据A、B两站的水位观测资料进行距离加权内插。

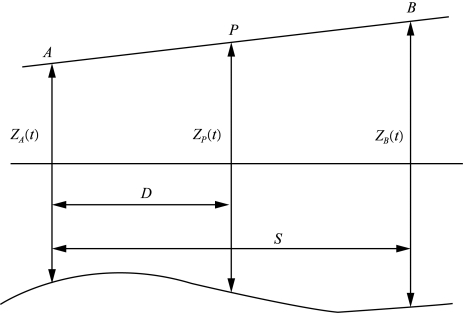
图9-15　双站距离加权内插法示意图

该方法也同样适用三站的情形，如图9-16所示，其假设的前提是三站之间的瞬时海面为平面形态。

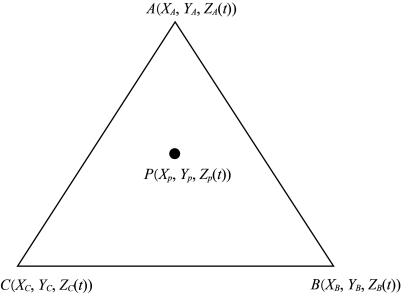
图9-16　三站距离加权内插法示意图

双站距离加权内插法的数学模型：

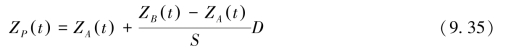
三站距离加权内插法的数学模型：

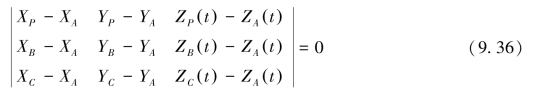
上面两式中，Z t（）为对应点（站）某时刻的水位值；X、Y为对应点（站）的平面坐标。

4.分带法

当测点距验潮站超出了验潮站有效控制范围时，可采用分带法、时差法及最小二乘法等进行水位改正。水位分带的实质是根据验潮站的位置和潮汐传播的方向将测区划分为若干条带，内插出各条带的水位变化曲线。对位于验潮站有效作用距离内的测点，可直接用该验潮站水位观测值进行水位改正；对不在验潮站有效作用范围内的测点，可内插出其条带的水位变化曲线，再根据该曲线进行水位改正（图9-17），分带所依据的假设条件是测区内潮汐性质相同，两站间的潮波传播是均匀的，即两站间的同相潮时和同相潮高的变化与其距离成比例。

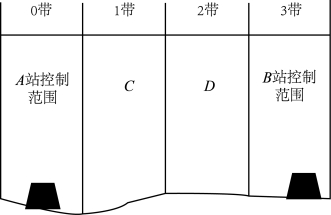
图9-17　双站分带示意图

同相潮时是指两站间的同相潮波点（如波峰、波谷等点）在各处发生的时刻，同相潮高是指两站间的同相潮波点的高度。如图9-18所示，假设A、B间潮波传播均匀，tA、tB为同相潮时，则两站间的潮时差τAB＝tB-tA，C站离A站的距离等于A、B距离的三分之一，所以C站的同相潮时（如高潮时）应等于tC＝tA+τAB/3，而C的同相潮高应在A、B同时潮高的连线上。

在潮波传播均匀的情况下，两验潮站之间的水位分带数K可由下式确定：

分带时，相邻带的水位改正数最大差值不超过测深精度δz，分带界线基本上应与潮波传播方向垂直，如图9-19所示，分带后根据某时刻A站或B站的水位数就可以推算出1、2、3等子带内某时刻的水位改正数。

当测区非狭长形，分带后各带仍无法用同一水位曲线描述该带内水位变化时，需要对条带继续分区。如图9-20所示，测区有3个验潮站，其水位分带分区方法为：先进行两两站之间的水位分带，这样在每一带的两端都有一条水位曲线控制，如在第II带，一端为C站的水位曲线，另一端为AB边的第2带的水位曲线。若两端水位曲线同一时刻的Δhmax值大于测深精度δz，则该带还需分区，将第II带分为II0、II1和II2，II1水位曲线由C站和AB边的第2带的水位曲线内插获得。

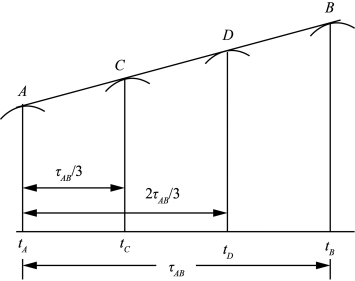
图9-18　同相潮时和同相潮高图

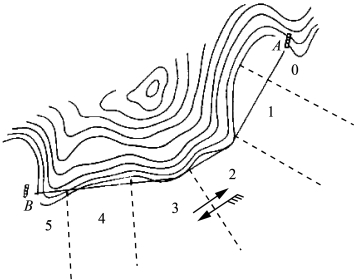
图9-19　双站分带示意图

对于更大范围的测区，验潮站的数量可能多于3个，其分带方法仍是以双站和三站分带为基础，对整个测区进行分带分区后再进行水位改正。在实际应用过程中，根据分带法的基本原理利用计算机编程即可完成水位改正工作。

5.时差法(www.daowen.com)

时差法水位改正是运用数字信号处理技术中相关函数的变化特征，计算两个验潮站之间的潮时差，从而求得测点相对于验潮站的潮时差，再通过时间归化，求解测点水位的一种方法，便于编程计算。

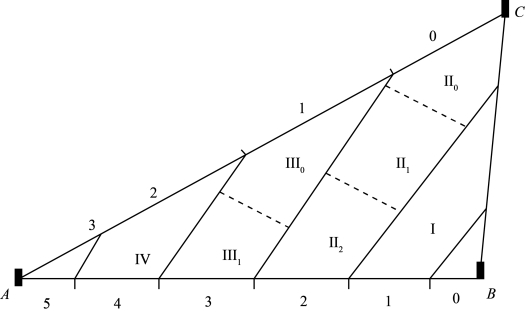
图9-20　三站水位分带改正法示意图

如图9-21所示，测区内潮汐性质相同，将两个验潮站A、B的水位视做信号，以验潮站A为基准，通过对两信号波形的研究求得两信号之间的时差，即为两验潮站间的潮时差，再根据待求点的位置计算其相对于基准验潮站的潮时差，并通过时间改化，最后求出待求点的水位改正值（谢锡君等，1988）。

设A、B两站潮位曲线的离散采样序列Xn、Yn分别为：

式中，t0为两验潮站的同步初始时刻，Δt为采样间隔，N为采样总个数，则得到两站的水位曲线如图9-21所示。

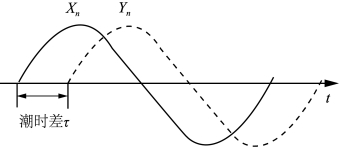
图9-21　两验潮站的水位变化曲线

首先分析两站水位曲线的相似程度，从离散数学原理可知，两曲线的相似程度是由一定采样值的相关系数决定的，相关系数R为：

越接近1，两曲线就越相似；越接近0，两曲线就越不相似。由于两验潮站之间存在潮时差，要确定两验潮站水位曲线的相似性，需对其中一站的水位曲线进行延时处理，如将Yn延时τ，使之变为Yτ＝TB（t0+nΔt-τ），则Xn与Yτ的相关系数Rτ为：

当τ为某一个值τ0，Rτ达到最大，说明Yn延时τ0后，与Xi最相似，τ0即为两站的潮时差，一般需通过迭代求解τ0。

同样，对于三个验潮站A、B、C的情形，只要满足时差法的条件，同样可求得三站之间的潮时差。若以A站为基准，则测点P（XP，YP，τAP）必位于A （XA，YA，0）、B （XB，YB，τAB ）、C （XC，YC，τAC ）三点组成的空间平面上，可以得到测点P的时间延时τAP为：

将各验潮站的观测时间改化为与测点P在t时刻对应的时间，即tA＝t+τAP，tB＝t+τAP-τAB，tC＝t+τAP-τAC，并分别求出对应时刻A、B、C各站的水位值ZA （tA）、ZB （tB）、ZC （tC）。根据假设条件，测点P [XP，YP，ZP （t）]必位于A [XA，YA，ZA （tA）]、B [XB，YB，ZB （tB）]、C [XC，YC，ZC （tC）]三点组成的空间平面上，从而测点P在观测时刻t的水位改正值ZP （t）为：

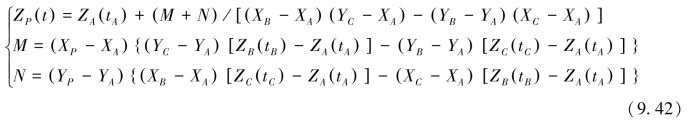
6.最小二乘拟合法

最小二乘拟合法与时差法类似，但在各点之间，除了计算潮时差之外，还考虑潮差比和基准面偏差。该方法首先对两个已知验潮站的水位序列进行最小二乘拟合，确定出两站之间的潮汐传递参数：潮差比γAB、潮时差τAB和基准面偏差εAB，再计算待求点相对于基准站的潮汐传递参数，进而内插求出待求点的水位（刘雁春等，1996）。

如图9-22所示，B站水位相对于基准站A为：

理论上，应该有：

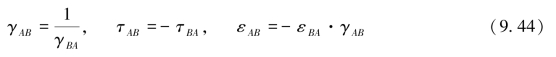
P为待求点，则

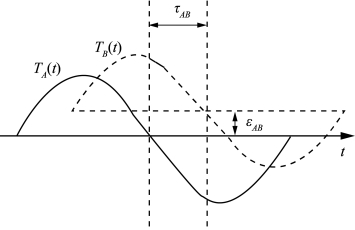
图9-22　水位曲线最小二乘拟合原理图

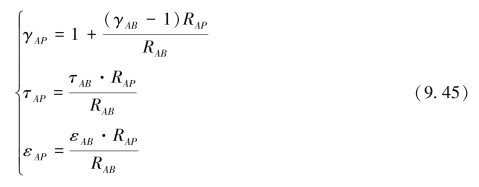
P点处的瞬时水位值为：

式中，TP t（）表示由验潮站A推估P点处的水位值。

最小二乘法同样适合用计算机编程计算，设A、B两站潮位曲线的离散采样序列为：

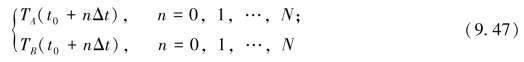
式中，t0为初始时刻；Δt为采样间隔，可取Δt＝5，10，20，30，60（min），N为采样总个数。

建立两验潮站潮位比较误差方程如下：

对上式进行线性化，并写成矩阵形式为：

其中，V为改正数矩阵，A为系数矩阵，X＝[Δγ，Δτ，Δε]T为未知参数改正数向量，L为常数向量。A矩阵的行元素具体为：

式中，γ0、τ0、ε0分别为未知参数γAB、τAB、εAB的近似值；T′A（t0+nΔt+τ0）为T对τ的导数。

L矩阵的行元素具体为：

根据最小二乘原则VTV[]＝min，可得：

实际计算中，需采用迭代法，通常初值取γ0＝1、τ0＝0、ε0＝0。在计算系数矩阵A时，需将离散数据连续化，一般采用函数插值技术，如二次样条函数插值。

总的来说，当测区范围不大，在一个验潮站的有效范围内，直接利用该站的水位观测资料改正；当范围较大，超过一个站的控制范围，采用两个站的水位观测资料分带改正；当两个站不能有效控制时，采用三个站的三角分带法改正。各种方法改正时，均需采用内插算法，只是内插的要素不同，一般采用线性内插、距离加权内插、时差法及最小二乘法，等等。具体的内插算法根据验潮站坐标是否已知、潮汐是否均匀传播等多种因素决定。