如前所述，水下地形测量主要是通过声波在水中的传播时间乘以声速来得到声波传播距离，从而计算水深及水底高程的一项工作。因此，声波在水中传播的速度，即声速的准确性对测深精度有着重要影响。声波在水中传播是不均匀的，声速与水介质的温度、盐度和压力相关，因而水中各点处的声速往往并不相等。对于水下测量设备采用的声波，一般为高频声波，在水中的传播轨迹可看做为声射线（简称声线），遵循Snell法则。如果水介质的温度、盐度和压力发生变化，入射角不为零的声线在水中的传播速度和传播方向也会随之变化。单波束测深仪采用垂直发射接收波束的工作方式，其声线传播方向基本不变，仅含距离误差的影响，因此受声速误差的影响较小；多波束测深仪各波束具有不同的入射角，如果声速存在误差，除中央波束外，其他各波束将受到声线折射和距离误差的双重影响，离中央波束越远，声线折射弯曲程度越大（李家彪，1999）。目前，声速改正的常用方法有声线跟踪法和面积差法。由于单波束测深声速改正可看做为多波束测深声速改正的一个特例，故本文主要对多波束测深声速改正进行介绍。

1.声线跟踪法

声线跟踪是利用声速剖面，逐层叠加声线的位置，从而计算声线的水底投射点（又称波束脚印）在船体坐标系下坐标的一种声速改正方法。声线跟踪通常将声速剖面N+1个采样点中相邻的两个声速采样点间的水层划分为一层，则声线传播经历的整个水柱可看作由N个水层叠加而成。若求得声线在每层的垂直位移和水平位移，通过叠加即可求得波束经历整个水柱的垂直位移和水平位移。声速在层内的变化一般分两种情况：当假设层内声速为常值时，声线的传播轨迹为一条直线，声线跟踪的计算过程相对简单，但相邻层的交界处声速会发生突变；当假设层内声速为常梯度变化时，声线的传播轨迹为一条弧线，更符合声线在水下的真实变化。

（1）基于层内常声速的声线跟踪

假设声速在第i层内以常速传播，层i上、下界面处的深度分别为zi和zi+1，层厚度为Δzi，θi、Ci分别为第i层的波束入射角和声速，如图9-3所示。

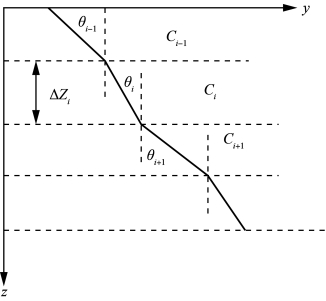
图9-3　基于层内常声速的声线跟踪

根据Snell法则，sinθiCi＝p，则波束在层内的水平位移yi和传播时间ti分别为：

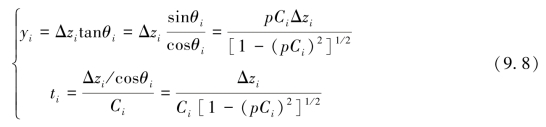
波束经历整个水柱的传播水平距离y和传播时间t为：

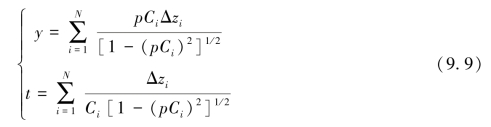
如果入射角为0（即单波束测深时），则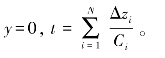

（2）基于层内常梯度的声线跟踪

假设声速在层i内以常梯度gi变化，其他假设与层内常声速的声线跟踪类似，则波束（初始入射角不为0）在层内的实际传播轨迹为一连续的、曲率半径为Ri的弧段（刘伯胜，2010，图9-4）：

式中，

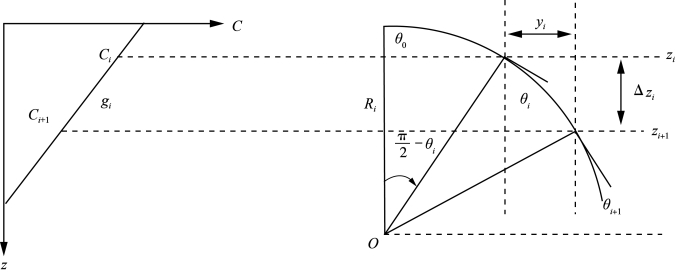
图9-4　基于层内常梯度的声线跟踪

波束在该层经历的水平位移yi和时间ti为：

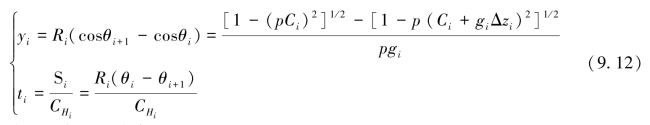
式中，CHi为层i内的平均声速。

若声线圆弧路径的微分单元采用圆弧形式，则平均声速为（陆秀平，2012）：

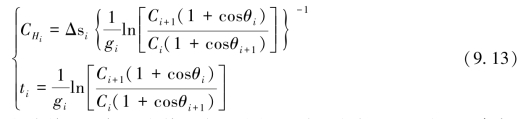
若将声线圆弧路径的微分单元近似取为其对应的弦长，则平均声速为（赵建虎，2002）：

如入射角为0，则声波在每层内的传播轨迹为直线，竖直向下，每层内的传播时间为：

（3）声线跟踪过程

层内声速特性不管采用哪种假设，声线跟踪的过程基本相同，具体如下：

①从换能器表面处开始，根据式（9.8）或式（9.12）计算声线在各层的水平位移和传播时间。

②计算前i层的声线传播时间总和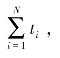与实际声线传播的单程时间T比较，根据比较结果来判断是否追加新的水层：

若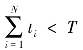，则重复过程①和过程②，继续追加水层；

若，则和为波束传播的深度和水平位移；

若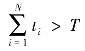，则多追加了部分水深和水平位移，退回至上一层。

一般情况下，跟踪至最后一层时，波束的水深位置不会恰好位于水层界面上，通常可由迭代法得到波束在最后一层内的水深和水平位移，再与前面各层的计算值相加，即可完成声线跟踪过程。

由上述可知，声速剖面的准确性直接影响着声线跟踪的精度，因此，在进行声线跟踪时所采用的声速剖面必须能够真实地反映测量水域水下声速的变化特性，遇到水域环境变化复杂的情况，应当加密声速剖面采样站、减小声速断面采样点间的层间隔。实际声线跟踪时还应考虑测船的瞬时横摇与纵摇对波束入射角的影响。

2.面积差法(www.daowen.com)

面积差法的主要思路是通过计算原始声速剖面与准确的声速剖面所围成的断面积分面积之差，从而计算出相对原始波束位置的改正值，达到声速改正的目的。首先需要理解等效声速剖面的概念。

（1）等效声速剖面

具有相同传播时间、表层声速及断面声线积分面积的声速断面族，波束的位置计算结果相同（Geng，1999；Kammerer，2000；赵建虎，2002）。因此计算波束脚印位置时，可以寻找到一个简单的常梯度声速断面替代实际复杂的声速断面（图9-5）进行声线跟踪（阳凡林，2008）。

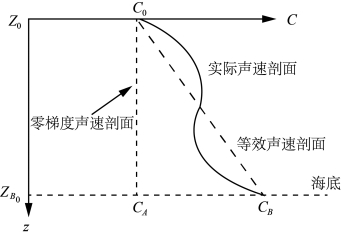
图9-5　等效声速断面

如图9-6所示，假设两个具有相同表层声速C0和初始深度z0的声速剖面，若对声速函数求深度上的积分，则可得到两个断面声线积分面积差：

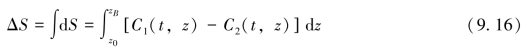
定义相对面积差为：

式中，C1（t，z）和C2（t，z）是两个声速剖面函数；zB是波束在水底的投射点。

由式（9.16）可以看出，两声速剖面之间的积分面积差与两声线积分上下限的深度及声速剖面相关。当εS＝0时，两声速剖面与坐标轴所围成的面积相等，由两声速剖面计算出的深度和水平位移相同，这时称其中一个声速剖面为另一个的等效声速剖面。实际声速剖面是一个随空间、时间变化的复杂函数，若找到一个相对简单的等效声速剖面进行声线跟踪，将提高计算效率。

（2）相对面积差法

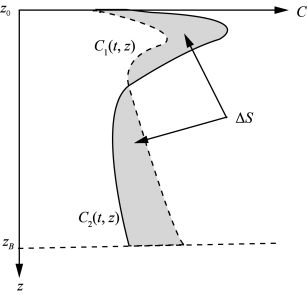
图9-6　两声速剖面积分面积差示意图

相对面积差法是一种先依靠一个相对简单的参考声速剖面（如零梯度声速剖面）计算波束水底透射点位置，再根据参考声速剖面与真实声速剖面的面积差计算波束位置改正量，从而得到波束水底投射点正确位置的声速改正方法（赵建虎，2002）。如图9-7所示，假设在水层i，实际声速剖面与零梯度声速剖面的积分面积差为ΔSi，这里讨论ΔSi引起的波束水深和水平位移的变化（也可称为改正量），假设条件和各符号的含义同常梯度声线跟踪。

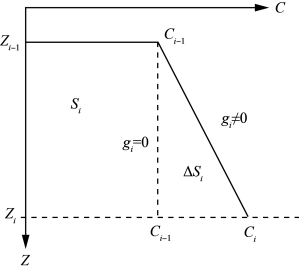
图9-7　层内常声速和常梯度声速剖面面积差示意图

考虑实际声速剖面gi≠0时，波束经历第i层水层时的水平位移yi、深度zi为：

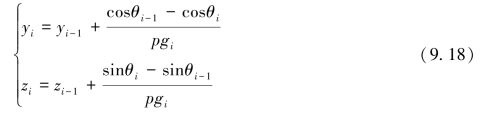
当仅考虑常声速部分，即gi＝0时，水平位移深度为：

如果仅采用gi＝0的声线跟踪结果作为最终结果，波束位置归算精度肯定不能满足要求，但直接采用真实声速剖面进行声线跟踪，在层数很多时计算效率又不高。为了既简化计算又提高计算精度，可在此基础上，采用面积差法求得波束位置改正量。还有一种情况利于采用面积差法，就是在多波束测量时，声速代表性误差普遍存在，更准确的声速剖面是事后得到的，这时也可在原始声速剖面归位的基础上计算改正数，得到更准确的波束位置。

根据图9-7，相对面积误差εsi为：设利用gi＝0时声线跟踪结果带来的水平和深度相对误差为：

根据Snell法则和式（9.20）有

将式（9.13）、式（9.18）、式（9.19）、式（9.20）、式（9.22）带入式（9.21）整理得和分别为：

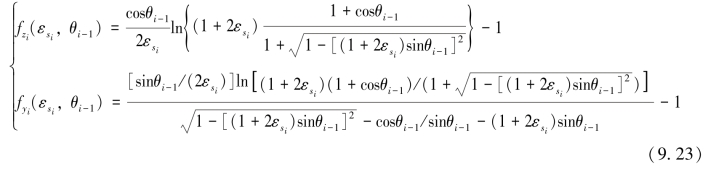
从式（9.23）可以看出，层i内的水平和深度相对误差只与此层的入射角和积分面积差有关，与其他参数无关。

由式（9.21）变换可得到补偿层内常声速计算误差的公式：

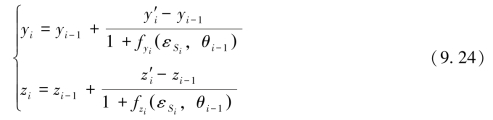
若将波束经历的整个水柱视为一层，声线的入射角、声速、换能器初始位置分别为θ0、C0和（y0，z0），可首先计算声速梯度为0时的波束初始位置，再根据相对面积差法计算波束位置改正数，从而得到波束的最终位置（zB，yB）：

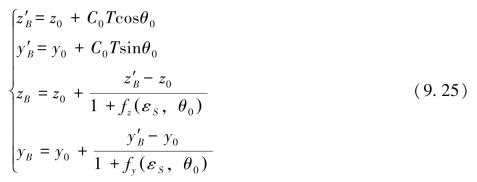
式中，T为波束单程旅行时间。

相对面积差法首先选择一条相对简单的声速剖面，根据面积差原理建立与实际声速剖面之间的联系，进而修正参考声速剖面的计算结果，简化了声线跟踪过程和计算的复杂程度。在实际多波束数据处理中，既可以通过新旧声速剖面的面积差来改正波束位置因旧声速剖面带来的误差，也可以针对准确但复杂的声速剖面，寻找其等效常梯度声速剖面利用相对面积差法来简化计算。