声呐图像通常存在大量的异常值、噪声和系统误差，在进一步利用前必须进行相应的处理。声图属于数字图像，因此许多常规的数字图像处理技术也适用于声图处理，但声图系统误差有其特殊性，一些滤波、增强技术并不适用于声图的处理，或者说效果一般，因此需要根据声图系统误差来源，采用针对性的方法进行处理。

采用常规的数字图像滤波技术可过滤异常值、平滑噪声，例如中值滤波、小波滤波、高斯滤波等。中值滤波是一种非线性滤波方法，优点是在移除异常值的同时不损害边缘特征，缺点是损害了图像细节，故许多研究者认为使用线性滤波方法效果更好。考虑到声呐图像一般采样率高，这时中值滤波的缺点基本可忽略，采用中值滤波能满足基本的需要（Bangham et al.，1990）。另外，一些基本的图像处理技术，例如直方图均衡化和对比度增强等，虽然改善了图像显示效果，但也改变了图像灰度间的相对比例，不利于其用于海底底质分类，因此这些方法应慎重使用。

原始的声呐图像，对应于回波强度，但并不直接反映真实的海底底质特征，因为回波强度除了受海底底质影响外，还受到时变增益、入射角、声照区面积、海底粗糙度等多种因素的综合影响，必须对回波强度进行处理，得到一个仅反映海底底质特性的观测量，称之为海底反向散射系数BSc（Backscatter Strength Coefficient）。一般对原始反向散射强度数据经过声信号传播损失改正、声线弯曲改正、入射角效应改正，再经过海底地形起伏及波束照射区面积改正、船底正下方镜面反射区影响改正后，最后得到海底反向散射系数，如图7-22所示。

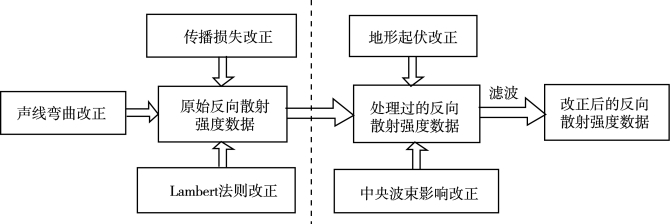
图7-22　反向散射强度数据预处理流程图（唐秋华，2006）

1.传播损失改正

声波在海水中传播时，受波阵面扩展、吸收及散射等影响，声强将逐步减弱。传播扩展损失是波阵面随距离变化而产生的声强衰减。设距离声源R1和R2处的两个波阵面面积分别为和在波阵面上所对应的声强为I1和I2，则扩展损失为：

在无损耗介质中，声波穿透波阵面的功率应保持不变，则有关系式：

因此有：

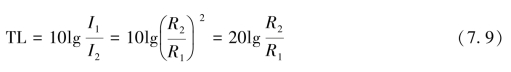
当R1＝1m时，

海水吸收是降低声能的又一因素，声波在海水中传播时，水中含有大量的自由离子，对声能具有较强的吸收作用。考虑海水的吸收，距离声源为R处的声强表示为：

式中，a为衰减系数；n为波束的传播形式，对于柱面传播，n＝1，对于球面传播，n＝2；I1为距离声源1m处的声强值。假设海底底质类型相同，不考虑声波散射损失，则海水中声能的传播损失为：

式中，第一项为波束的球面扩展损失；第二项为海水吸收损失，其中衰减系数a是频率f、盐度S、温度T和深度的函数。

当水文因素和信号频率无法改变时，衰减与传播距离（时间）存在近似正比例关系，传播距离越大，声强衰减越显著。为了得到远近场均匀一致的声呐图像，需对回波信号进行增益控制，包括时间增益控制、自动增益控制和手动增益控制，使声图具有最佳的效果（蒋立军，2002）。如图7-23所示，时变增益（TVG）是用来补偿随距离增大而下降的反向散射强度，使信号的输出在系统的动态范围内。不同的声呐系统，TVG函数不同。有些声呐系统中，TVG函数并不是连续的，而是由一系列具有一定步长的指数函数组成（Mitchell et al.，1989）。在后处理时，需要将阶梯状的函数改为连续性的函数。

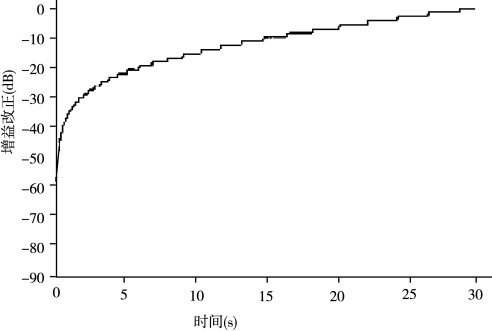
图7-23　时间增益步长

一些声呐系统增益估值准确度不高，例如6dB，反映在声图上即为航向不均衡，故对不同时间返回的声强还须进行精细改正。Johnson和Reed等通过计算每一列（航向）的改正系数来改正灰度的不均衡（Johnson，1991；Lingsch et al.，1995）：

式中，为整幅图像的灰度平均值；为第j列的灰度平均值，j＝1，2，…，n为波束号。

2.声线弯曲改正

波束的扩展损失和衰减损失与波束经历的传播路径密切相关。为了得到准确的传播损失TL，就需要对声波的传播路径进行追踪，即声线弯曲改正。关于声线跟踪的具体介绍，参见第9章。根据Snell法则，结合声速剖面和波束入射角，便可追踪到波束在每个水层的旅行路径，进而得到整个水层的传播路径，实现声线弯曲改正。

3.入射角效应改正

单位面积上的反向散射强度并不直接由声呐测得，而是通过一定的模型计算得到（Johnson et al.，1996）。通常反向散射强度在入射角θ＝0°～25°时有较大的变化；当θ＞25°时才满足Lambert法则：

(www.daowen.com)

式中，BSB表示单位面积海底固有反向散射强度，是海底类型和入射角的函数；BSo是入射角θ＝25°时海底反向散射强度值。

当θ≈0°时，BSB用BSn表示，是海底类型和粗糙度的函数，对于某一特定海底区域，该值通常近似为一常数；当0°＜θ＜25°时，海底固有散射强度随入射角呈线性变化（Hammerstad，2000）；当θ≥25°时，海底固有散射强度随入射角服从Lambert法则，如图7-24所示。

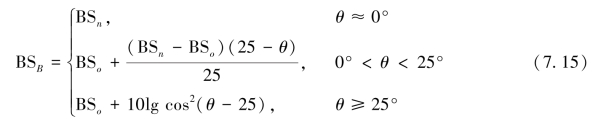
4.地形倾斜改正

声呐系统在进行回波强度计算时，假设海底地形是平坦的。然而，当海底并不平坦时，这个假设会引入误差，海底坡度越大，则引入的误差就越大。如果海底存在相应的数字高程模型（DEM）或者多波束测深数据，可据此计算出地形坡度角来改正入射角，重新计算反向散射强度。

设波束在平坦海底的入射角为θ，由于受到海底地形的影响，实际的入射角为θ′。

①当坡面同测量断面走向相同时，实际入射角θ′只是偏离了一个固定的海底坡度角β，波束在海底的实际入射角（特殊情况）为：

②当坡面同测量断面走向不同时，声照区的法线会偏离波束平面，任意坡面将产生二维入射角（一般情况）：

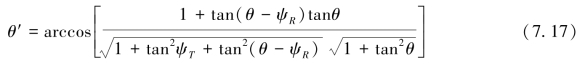
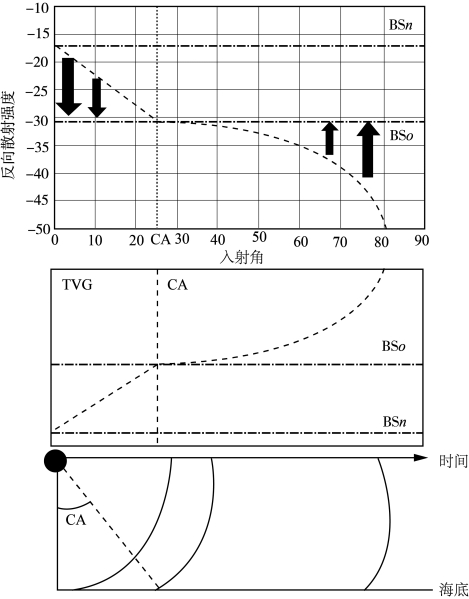
图7-24　回波强度、TVG与入射角的关系

式中，ΨR、ΨT分别为二维入射角在海底坡面沿横向和纵向投影的分量。

取坡面上三个点M1（x1，y1，z1），M2（x2，y2，z2），M3（x3，y3，z3），其中z1＞z2＞z3，则坡面方程为：

系数A、B、C可通过坡面的法向量确定，则坡度β为：

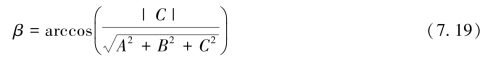
坡度β的计算精度主要受测深精度、波束分辨率的影响，因此建议采用与波束分辨率相适应的DEM来计算局部坡度，以及二维入射角在横向和纵向的分量。

5.声照区面积变化改正

反向散射强度BS取决于海底底质类型、地形条件和波束在水底的投射面积AE，它可表达为：

若海床平坦，根据是否镜面反射，波束脚印的面积AE为（图7-25）：

式中，τ为脉冲宽度；θT、θR分别为X、Y方向上的波束角宽度；c为声速。

图7-25　海底声照区面积计算

由于海底地形的倾斜，实际投射面积AE′与数据采集时平坦海底假设得到的投射面积AE会有所差别，其计算公式（Hammerstad，2000）为：

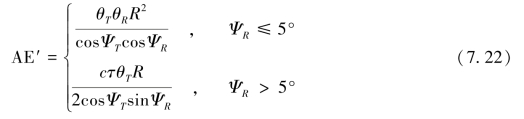
式中，ΨT，ΨR的意义同式（7.17）。