从第3章我们已了解到波束发射和接收具有指向性，图6-1是两个发射器间距λ/2时的波束能量图（Beam Pattern），左边为平面图，右边为三维图，可清楚地看到声能量的分布，不同的角度有不同的能量，这就是能量的指向性。如果一个发射阵的能量分布在狭窄的角度中，就称该系统指向性高。真正的发射阵由多个发射器组成，有直线阵和圆形阵等。这里只讨论离散直线阵，其他阵列可用类似方法推导得出。如图6-2所示，根据两个发射器的基阵可以推导出多个发射器组成的直线阵的波束能量图。

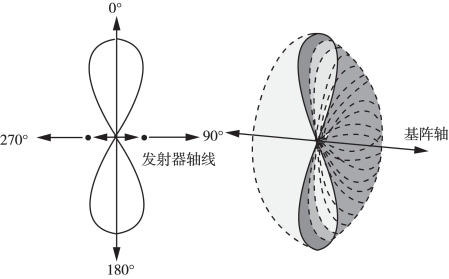
图6-1　两个发射器间距λ/2时的波束能量图

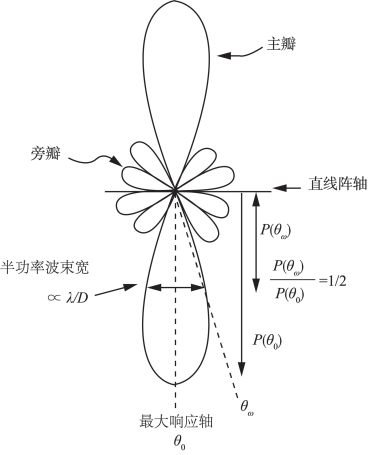
图6-2　多基元线性基阵的波束能量图

在图6-2中，能量最大的波束叫主瓣，侧面的一些小瓣是旁瓣，也是相长干涉的地方。旁瓣会引起能量的泄露，还会因为引起回波而对主瓣的回波产生干扰。旁瓣是不可避免的，可通过加权的方法降低旁瓣的水平，但是加权后旁瓣水平值降低了，波束却展宽了，因此需要在主瓣宽度和旁瓣水平间保持一个平衡。主瓣的中心轴叫做最大响应轴（Maximum Response Axis，MRA），主瓣半功率处（相对于主瓣能量的-3dB）的波束宽度就是波束角。发射器越多，基阵越长，则波束角越小，指向性就越高。

设基阵的长度为D，则波束角为：

从式（6.1）可以看出，减小声波长或者增大基阵的长度都可以提高波束的指向性。但是基阵的长度不可能无限增大，而波长越小，在水中衰减得越快，所以指向性不可能无限提高。

1.波束形成

米尔斯交叉（Mills Cross）阵在多波束换能器基阵中广泛采用，下面以其为例介绍波束形成原理。多波束换能器工作时，发射或接收基阵产生沿垂直基阵轴线宽、沿基阵轴线窄的发射或接收波束。发射和接收基阵以米尔斯交叉配置，发射波束与接收波束相交获得单个窄波束（图6-3）。该窄波束沿航向和沿垂直航向的波束宽度直接受对应发射波束和接收波束束控结果的影响。

图6-3　发射波束和接收波束相交获得单个窄波束（Hughes Clarke，2010）

从图6-3可知，由发射波束和接收波束交叉获得单个窄波束时，除主瓣波束外，还伴随有旁瓣波束。旁瓣有时会影响测深结果，因为其回波可能率先返回，因此波束束控时应尽量压制旁瓣，有利于突出主瓣，降低旁瓣的影响。图6-4显示了一个波束形成时，波束主瓣与旁瓣在海底的波束脚印。

图6-4　发射波束与接收波束相交效果示意图（Hughes Clarke，2010）

一个完整的发射接收周期（Ping）内，发射换能器只激发一次产生发射波束，接收换能器通过对接收基阵阵元多次引入适当延时获得多个接收波束。发射波束与接收波束相交获得多个窄波束，这个时间间隔很小，如图6-5所示。

2.波束束控

换能器阵发射或接收到的声波信号包括主瓣、旁瓣、背叶瓣，主瓣的测量信息基本上反映了真实的测量内容，旁瓣、背叶瓣则基本上属于干扰信息，其中旁瓣影响更大。旁瓣的存在会影响多波束的工作，过大的旁瓣不仅使空间增益下降，而且还可能产生错误的海底地形。为了得到真实的测量信息，减少干扰信息的存在，在设计多波束声呐系统时需采取措施尽量压制旁瓣，使发射和接收的能量都集中在主瓣，这种方法称为束控。

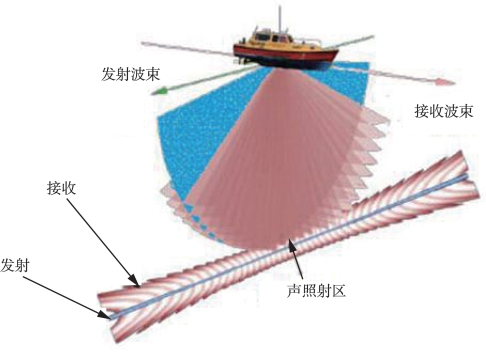
图6-5　发射波束与接收波束相交获得多个窄波束（Marques，2012）

束控方法有相位加权法和幅度加权法。相位加权指对声源阵中不同基元接收到的信号进行适当的相位或时间延迟。相位加权法可将主瓣导向特定的方向（波束导向），这时每个声基元的信号是分别输出的。幅度加权指给声源基阵中各基元加以不同的电压值。采用幅度加权法时，声基元的信号是同时输出的，只要保证基阵灵敏度中间大，两边逐渐减小，就能使旁瓣有不同程度的压低。

相位加权法束控可将主瓣导向特定的方向，并保持主瓣的宽度，但对旁瓣没有明显抑制；幅度加权法对旁瓣抑制效果明显，但会增加主瓣宽度。幅度加权通常采用的方法是对幅度进行三角加权、余弦加权和高斯加权。实践证明，高斯加权是比较理想的加权函数（秦臻，1984）。

下面以灵敏度均匀分布的连续直线阵的输出响应为例，介绍通过采用幅度加权实现波束束控的过程。

在采取幅度加权时，基阵的输出响应可表达为：

式中，L为直线阵的长度；A（x）为幅度加权函数；λ为波长；θ为波束角；dx为直线阵的微分单元。

令则式（6.2）可以改写成：

式（6.3）为傅里叶变换公式。从公式可以推断，基阵的输出响应等于对幅度加权函数A（p）的傅里叶变换。几种典型加权函数的傅里叶变换的输出响应曲线如图6-6所示。

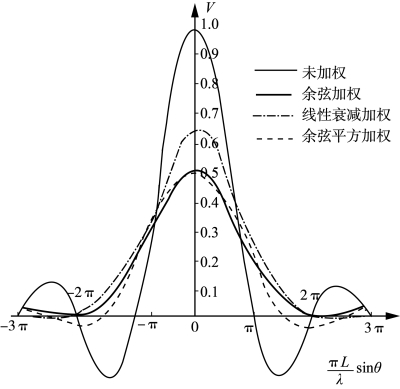
图6-6　连续直线阵经幅度加权变换后的输出响应

不同加权函数的采用使得旁瓣得到不同程度的压制。式（6.4）为加权函数A（x）的指向性曲线。

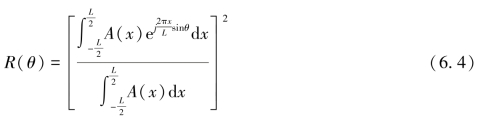
图6-7与图6-8为采用两种典型加权函数的束控效果图，图6-9为二项式加权函数与道尔夫-切比雪夫加权函数束控效果示意图。每幅图中，上图与下图分别为中心投影和等角投影。

由图6-6～图6.9可知，幅度加权后，旁瓣水平虽被压低了，但是主瓣输出响应的幅值变小了，同时主瓣的宽度变宽了，这是我们所不希望出现的结果（李家彪，1999）。为了保证幅度加权时主波束幅值仍与不加权时相同，需要适当加大基阵长度。数学上可以证明，对三角加权的情况，基阵长度应为2L，余弦加权基阵长度为πL/2，余弦平方加权基阵长度应该为2L，高斯加权基阵长应该为3λ/（2πsinθ）。

为了保证主瓣波束加权后达到预期效果，可应用幅度加权后的指向性函数，确定加权函数及其输出响应的关系。将式（6.3）改写为：

则

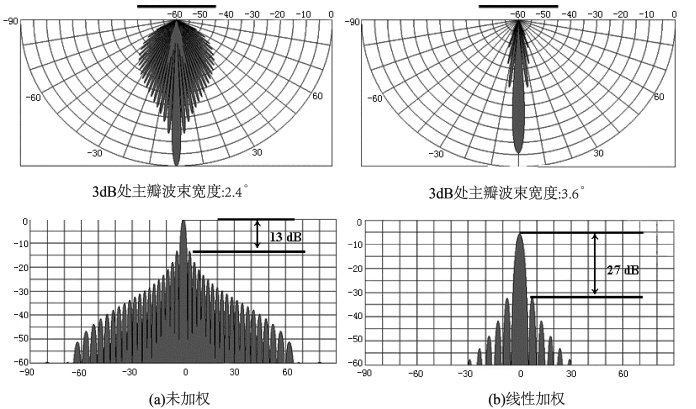
图6-7　线性幅度加权效果示意图（Hughes Clarke，2010）

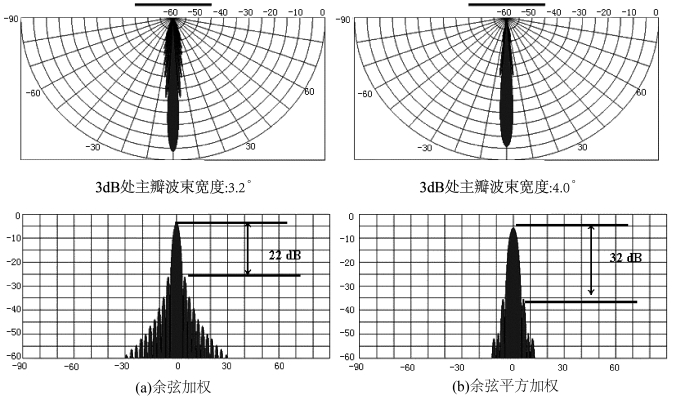
图6-8　余弦幅度加权效果示意图（Hughes Clarke，2010）

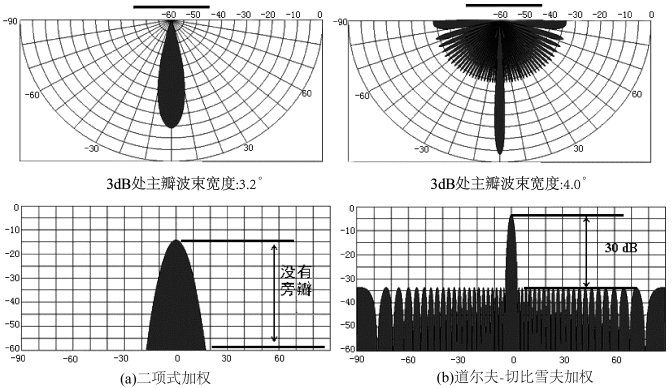
图6-9　其他幅度加权效果示意图（Hughes Clarke，2010）

式（6.5）和式（6.6）是基阵输出响应与加权函数之间的傅立叶变换关系式。当加权函数已知时，通过式（6.5）可以求解输出响应（即指向性），同样，当已知指向性时，可通过式（6.6）得到加权函数。

目前国际上已有许多压制旁瓣的加权函数，如Hanning加权、Blackman加权和道尔夫-切比雪夫加权等。在设计多波束系统时，各制造商可根据各种函数的加权特点和仪器的要求来选择不同的加权函数。例如选择二项式加权和高斯加权时，不会出现旁瓣，而选择道尔夫-切比雪夫多项式加权，可在给定旁瓣的条件下，给出最窄的主瓣（李家彪，1999）。

3.波束导向

下面以直线阵列多波束的形成为例，讨论多波束系统波束导向的原理，其他形式的基阵，如果存在波束导向，其原理基本都是相同的。

根据基阵形成波束的特点，当线性阵列的方向在θ＝0°时，各基元接收到的信号具有相同的相位，因此输出响应最大；当入射声波以其他方向到达线列阵时，若此时未对各基元引入适当延时，则无法获得最大输出响应。因此如要在其他方向形成波束，则须引入适当的延时，以保证各基元在输出信号时仍能满足同向叠加的要求（图6-10）。

如图6-11所示，接收阵由N个基元组成，当平面波束以入射角θ到达线列阵时，第（i-1）个基元比第i个基元接收到声信号时在空间距离（声程）上多经历了lsinθ，设声速为c，则这一距离引起的时间延迟为：

以最后一个基元即第（N-1）个基元为参考基准，那么第i个基元相对（N-1）个基元的声程为：

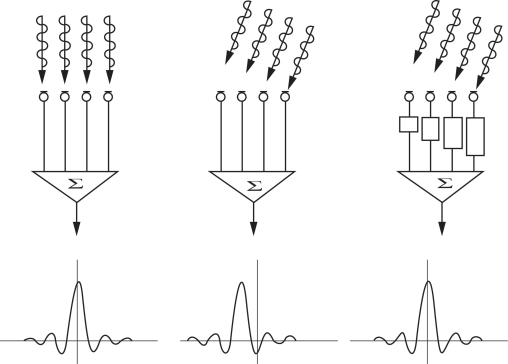
图6-10　线列阵输出响应与平面波束入射角和引入延时的关系示意图（Hughes Clarke，2010）

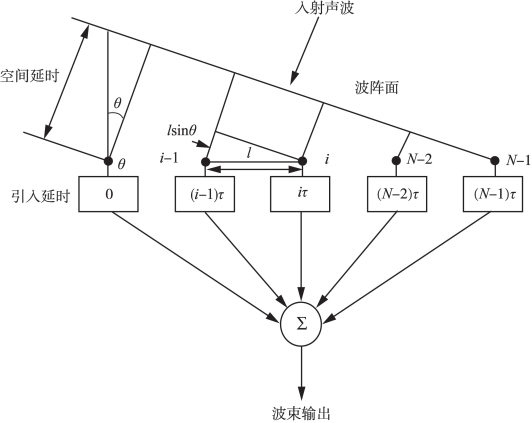
图6-11　N基元均匀线列阵波束θ方向形成示意图

由此产生的时间延时τ′i为：

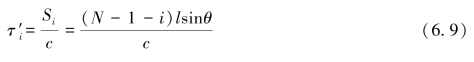
式中，i为基元序号，i＝0，1，2，…，N-1。

为了使入射声波波阵面能同时到达各基元，进行信号同相叠加后在θ方向获得最大输出相应，对各基元引入延时令

将声程引起的空间延时和引入的延时相加得到总输出延时τi为：即

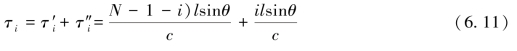
从式（6.12）可知，总输出延时τi与i无关，这意味着沿θ方向入射的声信号经过适当的延时处理后，同时到达各基元，因此声信号相加后必然出现最大输出响应。这种波束形成方法称为时间域波束形成。

由于波束数多，实时计算量大，为了加快波束形成速度，可利用快速傅立叶变换（FFT），FFT波束形成实际上是基于对相位的运算。

由频率域N基元线列阵获得第k个波束输出响应可表示为：

式中，v（k）为空间域第k个波束输出；Vi为频率域第i基元的输出电压；θ（k）为第k个波束的空间方位角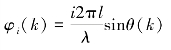；表示形成第k个波束时，在第i基元引入的相位延迟。

第k个波束输出可写成：

式中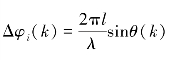，，表示形成第k个波束时，在相邻基元间引入的相位延迟。

取

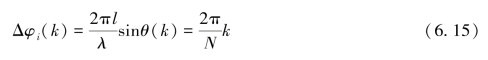(www.daowen.com)

则

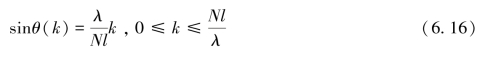
得

将式（6.15）代入式（6.14），得

式（6.18）即为离散傅立叶变换（DFT）公式，用来在θ（k）方向上利用FFT形成第k个波束输出。

对各基元输出的随时间变化的电压，利用FFT获得频率域基元输出Vi如下：

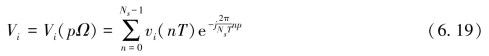
式中，Ns为时间采样数，n为时间采样序号，p为频率采样序号，Ω为频率分辨率，T为输入采样周期，vi（nT）为第i基元在时间采样序号为n时的输出电压，Vi（pΩ）为第i基元由时间域转到频率域在频率采样序号为p时的输出电压。

在频率域上利用FFT形成多波束的过程为：首先根据式（6.19）对各基元的时间采样利用FFT从时间域转到频率域，获得Ns各频率上的输出电压；再根据式（6.18）对各基元每个频率利用FFT从频率域转到空间域，最终获得θ（k）方向上第k个波束输出电压。

下面介绍波束在不同方向形成后的实际效果，以米尔斯交叉阵配置的多波束系统为例，通常由一个发射阵列和一个接收阵列组成，发射阵列的长轴沿航向放置，接收阵列长轴沿垂直航向放置（图6-12）。

图6-12　换能器阵安装图（Marques，2012）

理想情况下，发射阵元通过同时触发产生无导向的发射波束，如依次触发则产生有导向的发射波束（图6-13（a））；接收换能器通过对接收基阵各阵元引入适当延时，产生有导向的接收波束（图6-13（b））。图6-14显示了具有导向的发射波束与接收波束。

波束导向后，发射波束或接收波束的主瓣波束不再位于一个平面上（图6-15（a）），而是位于一定开角的锥面上（图6-15（b）），并且导向角越大，锥面开角越小（图6-15（c）），图6-15展示了波束余弦平方加权后的效果。

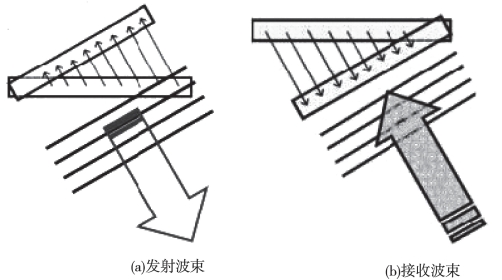
图6-13　波束导向过程示意图（Hughes Clarke，2010）

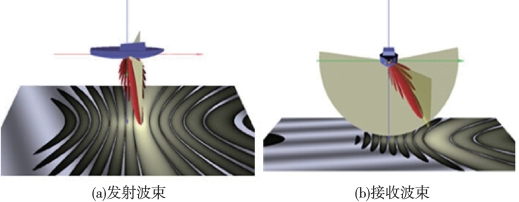
图6-14　波束导向效果图（Werf，2010）

图6-15　不同导向角的波束效果示意图（Hughes Clarke，2010）

4.多波束底部检测

多波束回波检测，一般采用幅度检测、相位检测以及幅度相位相结合的检测方法。当入射角较小时，波束在海底的投射面积小，能量相对集中，回波持续时间短，主要表现为反射波；当入射角较大时，波束在海底的投射面积也随之增大，能量分散，回波持续时间长，回波主要表现为散射波。因此幅度检测对于中间波束的检测具有较高的精度，而对边缘波束的检测精度较差（图6-16）。随着波束入射角的增大，波束间的相位变化也越明显（图6-17）。利用这一现象，在检测边缘波束时，采用相位检测法，通过比较两给定接收单元之间的相位差来检测波束的到达角。新型的多波束系统在底部检测中同时采用了幅度检测和相位检测，不但提高了波束检测的精度，还改善了Ping断面内测量精度不均匀所造成的影响（赵建虎，2008）。

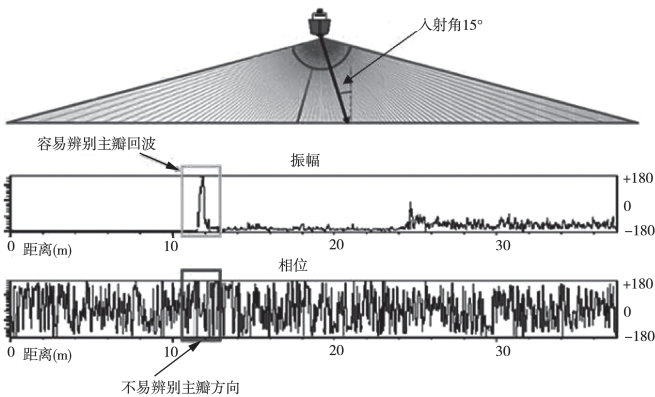
图6-16　中间波束振幅检测与相位检测对比（Hughes Clarke，2010）

多波束回波检测的目的是为了准确确定每个波束的TOA（回波到达时间）、DOA（回波到达角），并记录振幅或反向散射强度。其中前两个量唯一决定了后者。下面介绍TOA和DOA的确定方法。在多波束系统发展的过程中，有三种TOA和DOA的确定方法，分别为BDI（Bearing Direction Indicator，方位指示）、WMT（Weighted Mean Time，加权平均时间）和相位检测。BDI是指在FFT波束形成器输出的所有波束中准确地定位一个回波的DOA，然后计算该回波的TOA；而WMT先把DOA固定在每个波束的中心，然后再精确计算出每个回波的TOA（齐娜，2002）；类似于WMT，相位探测对每个固定的DOA计算其TOA，它通过相邻基元的相位差零点来确定TOA。当前BDI方法已基本由相位检测法替代。

（1）BDI处理方法

在一个发射接收周期内，设包含M个时间片（Time Slice），每个时间片分别表示为t1，t2，…，tM，相对的时间周期起点为t0；设有N个波束，每个时间片则可观测N个幅度值，θ1，θ2，…，θN，波束形成采用FFT处理方法，数据可表示为矩阵的形式，如图6-18所示。

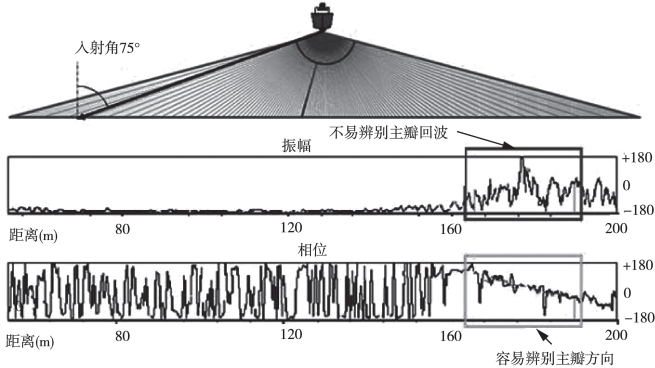
图6-17　边缘波束振幅检测与相位检测对比（Hughes Clarke，2010）

图6-18　单Ping回波强度矩阵

为防止旁瓣或海底混响等其他因素引起的回波噪声，对于每个时间片，使用一个动态阈值，也叫检测门限，高于阈值的幅度接受，低于阈值的幅度视为噪声。阈值由旁瓣水平和噪声水平决定，每个时间片均不同。将高于阈值的幅度值进行拟合，求得幅度的极大值，同时记下相应的角度值，就是该时间片对应的DOA，如图6-19所示。这样，每个幅度极大值对应另外两个数据：角度和时间，这三个数反映了波束发射到接收的过程，以击中（Hit）表示，即每个击中用这三个数据表示。

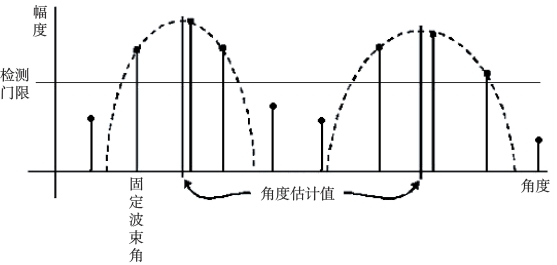
图6-19　单时间片中角度的精确估计（L-3 Communications SeaBeam Instruments，2000）

如图6-19所示，在一个发射接收周期内，将所有的击中以角度和时间表示出来，在每个波束范围内，计算平均时间tmean和方差σ，保留与tmean相差1倍σ内的击中，最后根据幅度加权计算出每个波束的DOA和TOA，在图6-20中表示为θB和tB。为了问题的简化，这里没有考虑姿态补偿。

（2）WMT处理方法

WMT首先固定一系列的波束角，这些波束角已经进行了姿态补偿。然后计算出每个波束角精确的TOA。因为姿态的影响，固定的波束角并不一定在波束轴中心。在每个时间片，都可得到每个固定角的幅度值，在整个发射接收周期内，可得到每个固定角的时序观测的幅度值，使用开始、结束门限和动态阈值，就可得到最后参与计算TOA需要的幅度值，然后按幅度加权就可得到精确的TOA。如图6-21所示，图中粗线即为计算TOA保留的幅度值，处于开始门、结束门外和动态阈值下的均被忽略，最后的TOA计算同式（6.16）。

（3）相位检测

相位检测方法与WMT检测方法类似，也是在给定回波DOA的条件下计算回波的TOA。该方法将换能器阵列分成两个具有部分基元相互重叠的虚拟子阵，子阵各自进行波束形成，如图6-22所示。

对相同波束号的回波信号提取每个时间采样对应的相位差。当相位差值为零时，该零相位差交叉点所在时刻即为预定波束方向回波的TOA估计。图6-23（a）中AB线表示给定的回波DOA，对该方向下的每个时间采样计算相位差，将时间采样的相位差成图（图6-23（b）），在零相位差交叉点处（CD线表示零相位线）获得该回波在给定DOA下的TOA估计，并且对应每个给定的DOA只有一个TOA估计。

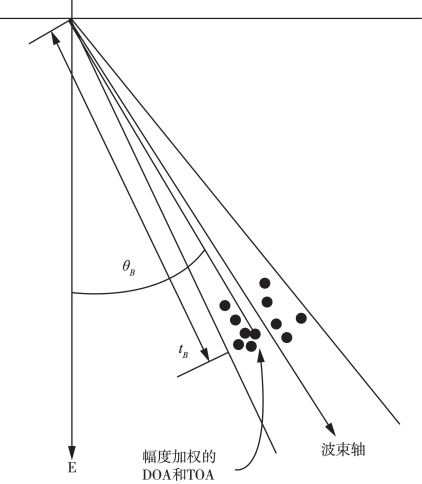
图6-20　幅度加权平均一个波束的DOA和TOA（L-3 Communications SeaBeam Instruments，2000）

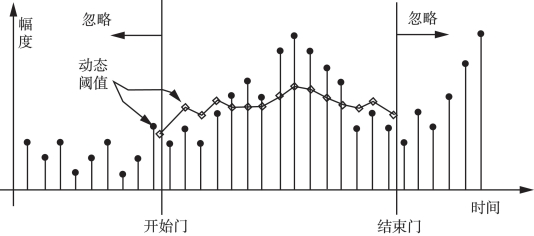
图6-21　参与计算的幅度值（L-3 Communications SeaBeam Instruments，2000）

由于BDI法已基本被相位检测法替代，具体的检测方法主要是WMT或相位检测法，至于选择哪种检测方法，要根据具体情况来决定。对于镜面反射，反射强度大，回波脉冲尖，持续时间短，此时相位检测不太适用，因为很难通过相位差零点来确定正确可靠的TOA，因而采用WMT方法；相反，在非镜面区，反射强度小，回波脉冲平缓，持续时间长，此时WMT不太适用，因为很难准确地计算回波时间，因而采用相位检测方法（阳凡林，2006）。

图6-22　相位检测法的虚拟子阵（Hughes Clarke，2010）

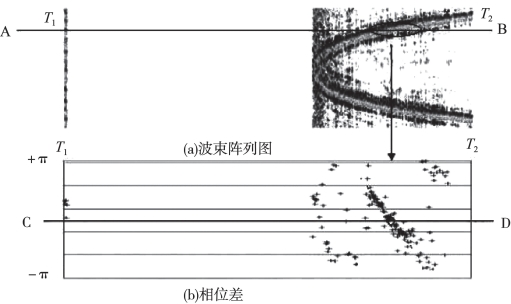
图6-23　零相位交叉点确定TOA（Hughes Clarke，2010）

5.实时运动补偿

由于测船在海上会受到风浪、潮汐等因素的影响，所以在测深过程中测船的姿态随时都在发生变化。实时运动补偿就是指测船的摇摆运动进行分解，通过控制发射或接收波束反向转动补偿因测船摇摆引起的声基阵转动，从而使发射或接收波束面相对地理坐标系稳定（白福成，2007）。以前的多波束系统大多采用后置处理的方法，现在很多新型的多波束仪器开始采用实时运动姿态补偿技术，从而较好地解决了测深过程中测船姿态变化引起的测点不均匀的问题。

当船只受横摇影响时，条带边缘会随横摇角的变化出现相应位置偏移（图6-24（a）），要达到全覆盖，此时需要减小测线间距才能满足要求。引入实时横摇船姿补偿后，可明显消除条带边缘偏移现象，不需减小测线间距（图6-24（b））。

当船只受纵摇影响时，沿航迹方向的前后条带间距随纵摇角变化，出现前后条带存在间隙或多余覆盖的情况（图6-25（a））。引入实时纵摇船姿补偿后，可消除这种现象（图6-25（b））。

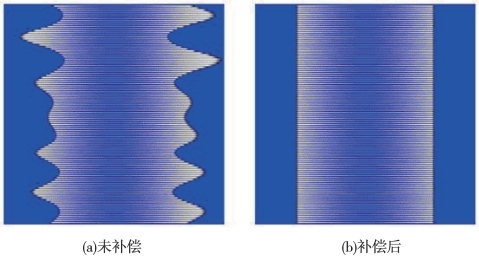
图6-24　横摇补偿前后对照效果图（Hughes Clarke，2010）

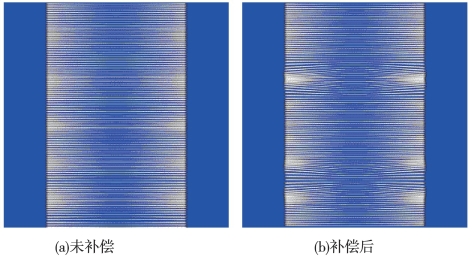
图6-25　纵摇补偿前后对照效果图（Hughes Clarke，2010）

多波束测量时，除了受到横摇与纵摇的影响，还受到首摇的影响。当考虑首摇影响时，出现周期性的条带偏转现象（图6-26）。

图6-26　首摇对测深影响效果图（Hughes Clarke，2010）

横摇实时补偿时，在固定扇区开角情况下，通过接收时刻测船的横摇角度，对接收基阵各基元引入适当延时，使接收波束导向以补偿横摇影响，从而实现波束方向的稳定（图6-27）。

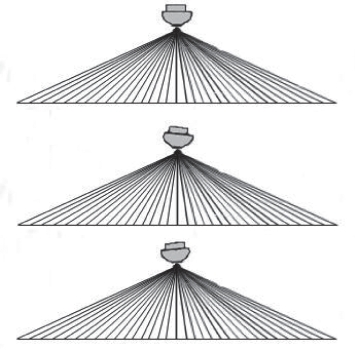
图6-27　横摇补偿波束方向效果图

纵摇实时补偿时，通过获取发射时刻测船的纵摇角度，对发射基阵各阵元依次触发产生具有导向的发射波束，补偿纵摇角度，从而保证发射波束保持在船下方近似垂直的平面内（图6-28），最终获得沿航迹方向密度均匀的条带。

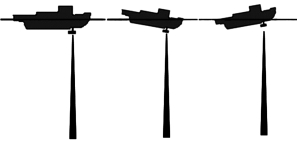
图6-28　纵摇补偿波束方向效果图（Hughes Clarke，2010）

对于首摇实时补偿，这时依靠单扇区进行统一的发射导向是无法实现的，多波束系统可通过多扇区特性进行实时首摇补偿，当纵摇较大时，纵摇实时补偿也须分成多扇区进行，每个扇区补偿角不同。以EM300多波束系统为例，其可产生9个频率不同的扇区。相邻扇区脉冲发射间隔只有几毫秒，因此可认为所有脉冲信号同时在水体中传播。首摇实时补偿时，每个扇区根据发射时刻首摇角度（有时还同时考虑纵摇角度）进行发射波束导向，获得具有一定首摇补偿的单个扇区，经过连续发射获得9个单独且相邻的扇区（图6-29），最终获得近乎不受首摇影响的条带。

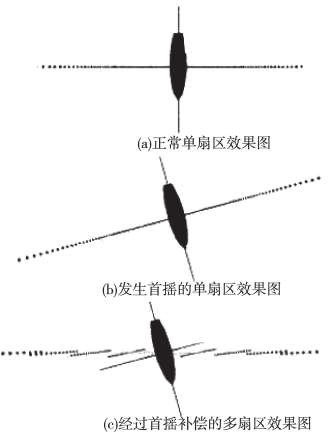
图6-29　单扇区与多扇区效果对比图（Hughes Clarke，2010）

多波束测量过程中，测船通常同时受到横摇、纵摇和首摇的影响，实时运动补偿时根据姿态传感器获得船的瞬时姿态，对发射和接收换能器基阵各阵元同时引入适当延时，使发射波束或接收波束具有一定导向角以补偿船姿影响，从而获得较稳定的波束。图6-30从左到右依次显示了未补偿、仅实时横摇补偿、实时横摇和纵摇补偿、同时实时横摇、纵摇和首摇补偿的效果对照图。经过实时船姿补偿后，基本上消除姿态变化对条带测量的影响，使相邻Ping条带边缘波束位置偏移较小，前后Ping间距基本均匀，从而易于实现全覆盖测量的要求。

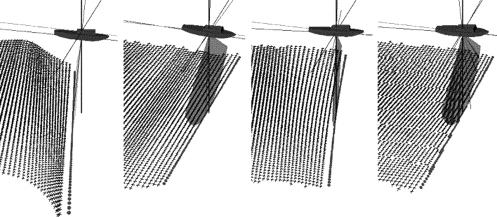
图6-30　实时姿态补偿效果对照图（Hughes Clarke，2010）