根据式（5.2），严格的回声距离应通过积分过程确定，然而声速在传播的短时间内变化规律通常是极其复杂的，通常视为声速随深度变化。因为单波束测深基本可保证垂直向下发射声波，且通常认为在小范围内水介质的温盐水平分布均有均一性，因此不考虑声线的弯曲影响。正是在这一前提下，往返声波可视为基本沿同一路径传播，所测深度为声波传播距离的二分之一。

据积分中值定理，回声距离的积分公式可改写为：

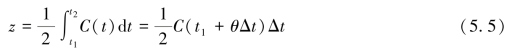
式中，C（t1+θΔt）为声波传播的等效均匀声速，θ∈[0，1]。

然而式（5.5）仅适用于理论分析，而无法确定准确的等效声速值。在实践中，通常在测深工作前后及期间通过分层测定影响声速的海洋物理因素或沿垂直剖面的直接离散声速，确定一系列深度点的声速值。在每层常声速或常梯度声速的假设下确定海区的等效平均声速。

在水介质铅直剖面内，实际声速、等梯度假设下的声速以及等速假设下的声速变化结构如图5-4所示。

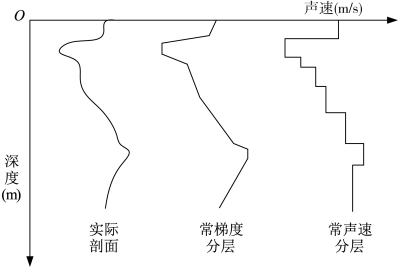
图5-4　声速垂向变化示意图

若在水中，取不同深度（采样设备自带深度标记）zn处的声速采样值，通过直接或间接方法得到对应点声速值Cn，假设总采样数记为N+1，则平均声速可按这些点所划分的N个水层声速的距离加权平均值确定。

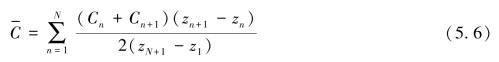
这种平均计算显然是基于每层声速随深度的常梯度变化的假设。当水层划分较细致时，可以认为是准确的等效声速。

利用等效平均声速，则测定的水深可简写为：

测深仪通常设定一个参考声速Cm，则仪器输出的测深值为：(www.daowen.com)

于是，仪器输出的测深值与真实深度之间将存在偏差，且这种偏差呈系统误差性质，会随着深度的增大而增加。

比较式（5.7）和式（5.8），可得：故对测定深度所施加的声速改正数为：

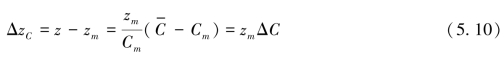
计时误差对深度测量理论上也存在影响，但考虑到测深仪依据的是回声测深原理，采用时间差而不是时刻信息进行时深转换。因此，在同一时间控制系统下，这一误差可忽略不计。在此前提下，鉴于平均声速与严格意义的积分等效声速，而且声速测定的时间与测深时间不匹配、位置不一致也会使得所用声速存在一定误差，因此可根据式（5.8）对声速误差的影响做出进一步估算。

声速将以相对误差的形式对测深结果产生影响，但目前测深仪的标称相对测距精度通常为5‰，因此，只要进行合理的声速观测，将平均声速的误差控制在2～3m/s以内，声速以1500m/s计，所产生的深度误差基本可控制在2‰，对单波束测深的误差影响可忽略不计。

传统的测深技术还需关注转速误差的影响，这是因为传统水深回波信号记录采用模拟方式。记录仪指针在旋转过程中，根据收发信号触发，在记录纸上绘制回声记录曲线，如图5-5所示。

记录指针的转速应与声速具有合理和严格的比例关系，否则将引起误差，必须改正，即转速误差改正。显然转速误差可归结为声速误差处理。现代测深仪通常采用模拟和数字两种记录方式，模拟记录结果主要用于对存疑数据校核，正常情况下以数字记录为主。因此，在此对这种误差仅作附带说明。

图5-5　回声测深仪模拟记录示意图