1.位置函数及位置线方程的概念

无论何种定位形式，基本原理都是获得两个以上观测量，这些观测量可以描述为位置的函数，同时通过观测又可获得对应的观测值，因此，综合解算两个以上具有已知观测值的坐标函数方程，即可求得待定点的坐标。这就是各种定位方法实施定位的一般性原理。某一观测值与坐标之间的函数关系式即观测样式和观测信息对应的等值线方程，若假定观测量对应的等值线在二维坐标基面上描述，使用两个观测量，即通过寻找两个等值线的交点，就可以图解方式或解析方式求得待定点坐标，此即二维坐标面上交会定位的基本思想。前述前方交会、后方交会以及距离和方位定位、双曲线定位这类依据地（海）面观测量的二维定位问题均据此原理实现位置确定。当然，需要三维位置时，必要观测量与坐标维数等同地增加。本部分仍讨论二维定位问题。

在平面坐标系中，位于坐标平面的观测量可表示为：

而在大地坐标系（地理坐标系）中，位于坐标面（近似地视为椭球面）的观测量表示为：

其中，（X，Y）、（B，L）分别为定位点的平面坐标和大地坐标。

以上二式即观测信息量（方程左侧）和作为参量函数（方程右侧）的关系方程，以所得观测量为常数，方程所描述的是观测形式所确定的观测量等值线方程，称其为位置函数。位置函数根据不同的观测形式，可以是线性函数，也可以是非线性函数，线性函数为非线性函数的特例，因此所有位置函数均可归为非线性函数。

将观测函数对应的等值线称为位置线，因为观测量不可避免地存在误差，并向由相应的等值线交会计算的点位传递，以微分形式表示这种误差的影响，将观测方程线性化得：

式中，（X0，Y0）为由观测量计算的点位坐标；dX＝ΔX，dY＝ΔY是由于观测误差du＝Δu引起的坐标分量误差。

在后续讨论中，为简化表示，将导数取值的对应点符号略去。

公式（4.28）也可写为：

考虑位置函数是观测量的标量函数，引入标量函数梯度的概念和相应的数学符号，则有：

式中，均为等价的函数u的梯度表示方式；i、j分别为两个坐标轴方向的单位矢量。

梯度的模为：

梯度模的含义为标量函数变化量的极大值，对于位置函数，即位置函数等值线或定位位置线沿其方向的变化率，而将该方向的极角（在测量常用平面坐标系中即方位角）记为τ。

据方向导数与梯度的关系：

则观测量变化或误差与位置变化量的关系可进一步描述为：

对于在地理坐标系上，由经纬度表达的观测量函数方程（4.27），存在观测函数关于曲线坐标的方向导数或变化梯度表达式。

一般将观测函数的这种线性化表达式称为位置线方程。

2.定位中误差普遍式（统一公式）

在二维坐标面上实施海上定位，当存在两个观测量时，观测量与坐标的微分关系式写为如下方程组：

进一步可将观测量变化引起的可能处于任意方向的位置变化量改写为位置函数法向（梯度方向）变化的形式，即

这样描述的位置线方程为归一化形式，也称为位置线方程的法线式。

若观测向量u＝[u1　u2]T的误差方差阵为：

则二等值线法线观测向量的投影n＝[n1 n2]T的误差方差阵为：

据式（4.35），有

其中，ω＝τ2-τ1，为位置函数梯度方向的夹角，同时亦为位置函数（或位置线）在定位点处的夹角。

根据误差传播律，定位点误差向量Z＝[dX dY]T的方差阵为：

在两个观测量不相关，即σ12＝0的条件下，可推得点位坐标方差阵各元素的具体形式为：

通常情况下，点位坐标的精度由点位方差或点位中误差衡量，而点位方差为任意二垂直方向上方差之和，为不变量，即不因坐标系选择的不同而不同，表示为σ2P＝σ2X+σ2Y，由此，将所求得的坐标方向的方差公式代入点位方差计算式，得点位中误差表示的精度公式为：

此式称为定位（点位）中误差的普遍式，它反映了定位精度（点位中误差）与观测量中误差、位置函数在定位点的梯度以及两条位置线几何配置（交会角度）之间的关系。已知观测量的类型、观测值的精度（中误差），即可估算定位结果的精度，通常用于定位的技术设计和定位成果的精度估算。

一般情况下，认定用于定位的不同观测量的误差不相关是合理的，常规地面观测量（方位、角度、距离等）均通过独立观测过程获得，必然是不相关的。而就岸基无线电定位而言，岸上的无线电发射台通常称为主台和副台，即在主台的控制下形成定位基准台链。其中主台的控制作用主要体现在信号发射相位的同步，并且在船台处测得的距离差（相位差）观测值来源于两个副台分别与主台信号的差分，因此两个观测值的误差将存在一定程度的相关度。此时需考虑σ12≠0的情况，可导得：

以上定位精度均是以点位中误差为衡量指标，所需各类观测量的精度可取观测样式对应的中误差经验值，这些经验值主要根据采用仪器的精度标称值及观测条件确定。

从定位中误差的普遍式可以看出，两条位置线的交会角度对精度指标发挥重要的支配作用，当交会角为90°时，cscω＝1；而当交会角偏离90°时，该系数值将随偏离程度而增大；当时，即位置线交角降至30°时，点位中误差将增大到最优状态的2倍。因此，一般的定位要求是位置线交角大于30°。

3.多种定位模式的精度评估公式

用常规地面观测技术实施海上定位，可采用多类观测量的组合模式，相应的线性化观测方程（位置线方程）和点位中误差计算公式介绍如下。

（1）前方交会的点位精度

观测量（方位）与坐标参量的函数关系为：

式中，i为控制点编号，i＝1，2，…，且通常可由字母A、B标记；带有下标P的坐标指待定点坐标。

方程的线性化形式为：

由方程的线性化系数可知，位置线的梯度模为（弧度/m或弧度/km），因此前方交会的定位中误差估计公式为：

在此，σ′为方位观测的中误差，以分为单位，ρ′为1弧度所对应的角分值，即ρ′≈3438′。当测点到控制点的距离以km为单位，点位中误差以m为单位时，式（4.45）可进一步明确为：

（2）距离交会的点位精度

通过二（水平）距离观测量实施交会定位式，因为二观测量的等值线均为圆，因此称为圆定位。这种定位方法所应用的位置函数表达式为：

方程的线性化形式为：

而距离函数的梯度模为1（无量纲），因此点位中误差的基本计算公式为：(www.daowen.com)

二距离交会定位的中误差的量纲与距离中误差的量纲相同。因为距离测量仪器的测量中误差通常存在与距离成比例的部分，所以在此取两个距离观测量的精度不等。当定位点距二控制点的距离近似相等，或不顾及距离观测量的乘系数误差时，点位中误差公式可简写为

（3）方位距离定位的点位精度

采用一个方位观测量与一个距离观测量，即用方位和距离两类位置函数实施海上动点定位较为常用，根据前述给出的位置函数及其线性化形式，顾及两类位置函数的梯度，立即可得一方位一距离定位的点位中误差公式：

式中，r表示定位点与方位观测量对应控制点的平面距离。

应用方位距离定位模式，通常在单一控制点观测到待定点的距离和方位，这种模式对定位作业不仅便于组织实施，而且是在电子全站仪广泛应用的技术条件下，更具有方便性。此模式下，两类位置线正交，即ω＝90°。若距离和方位观测的中误差分别以m和分为单位，观测的距离以km为单位，则点位中误差计算的实用化公式为σP＝

（4）测角后方交会的点位精度

由定位点P观测控制点i、j之间的水平角（定位点与控制点高度不等时，需实施倾斜平面内的观测角向水平角的归算），水平角α与定位点和控制点坐标的关系式，即位置函数方程式为：

相应的线性化形式为：

据此线性化方程的未知数系数，可推得角度函数的位置线梯度模为：

在海上定位应用中，测角后方交会通常对三个控制点目标观测两个相邻的水平角（即三标两角法），且角度观测的精度相等，中误差记为σα，此时不妨假定所照准的三个标志点按A、B、C顺序排列，并替换式（4.52）、式（4.53）中各量的下标，则后方交会定位的点位中误差为：

同样，当距离以km为单位，测角中误差的单位取为角分，则定位中误差可由下式计算。

（5）侧方交会的点位精度

侧方交会分别在定位点测定角度，在一个控制点测定方位，不妨将方位观测的控制点记为A，则根据方位和角度观测误差及相关的距离信息，可知侧方交会的点位中误差公式为：

当距离以km为单位，角度和方位测量的中误差单位取为角分，则定位中误差可由下式计算。

（6）距离差定位

以两个距离差实施海上定位是卫星定位技术之前广泛应用的远海定位技术，因为距离差观测量对应的位置函数为双曲线方程，所以距离差定位常称为双曲线定位。而距离差的测定则主要通过地面无线电定位系统的脉冲传播时间差或无线电波自发射到接收的相位差观测实现。

在平面坐标系内，定位点P距处于一对控制点的无线电波发射台i、j的距离差函数表示为：

相应的线性化形式为：

根据线性化方程的系数，可导出双曲线型位置函数的梯度模为：

式中，α为测点相对两控制点（双曲线焦点）所张开的水平角。

在无线电定位中，通常假定不同路径的电磁波相位差观测量精度相等，记距离差测量的中误差为σΔr，则由两对（通常一个无线电发射台站公用）双曲线交会的点位中误差为：

式中，α1、α2分别为测点对相应的岸台基线所张的水平角。

经推导表明，就三个岸台构成的双曲线定位台链而言，定位点处双曲线的交会角为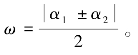

而考虑到距离差观测量的相关（相关系数ρ），双曲线交会的点位中误差公式进一步改写为：

在此所讨论的双曲线定位精度估算公式仅适用于近程无线电定位系统，主要是因为这里的公式是在平面坐标系中导出的，事实上在这种近程无线电系统的应用中，也必须对测定的距离差进行必要的归算，化算为投影平面上的距离差。而对远程定位系统，必须根据椭球面上的双曲线方程实施定位与相应的精度评定。

4.定位的误差椭圆

更细致的位置精度刻画需要采用误差椭圆，以反映在不同方向上中误差的变化，并对应于一定的概率意义。根据式（4.39）中点位二维坐标向量方差阵的元素，可确定误差椭圆的对称轴（长、短半径）及所在方向。中误差极值（最大和最小）方向由下式确定：

式中：θ为误差椭圆长（短）半轴与X轴方向的夹角，对于测量常用坐标系，实际上为误差椭圆对称轴的方位角，由该正切表达式解算出的特征方向为相互正交的两个方向值θ1和θ2，至于哪个方向对应长半轴或短半轴，需根据方差和协方差信息具体分析。

而长、短半轴的量值为：

其中，而上式根式中的“+”、“-”号分别对应于极值中误差取误差椭圆长半轴和短半轴的情形。

顾及点位坐标矩阵的具体表示：

所以误差椭圆的长短半轴长度为：

5.具有多余观测的平差处理与精度评定

对于海上的二维定位问题，当存在3个以上观测量时，则可根据多个位置函数的线性化方程，通过最小二乘平差方法计算点的位置，并对定位点的精度做出评定，即可通过下列计算流程。

由两条位置线交会原理算得定位点坐标，作为位置函数线性化，进一步进行平差计算的近似坐标。

根据近似坐标列出各观测函数的线性化误差方程：

式中，vi为观测值的改正数；为坐标改正量的平差值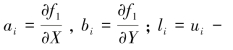；，其中（X0，Y0）为待定点坐标的参考（近似）值，且线性化方程的系数ai、bi所对应的偏导数也均据此坐标信息计算。

将式（4.67）所列各位置函数的线性化方程整合改写为矩阵表达式：

式中，V为改正数向量；；A为由线性化系数构成的系数矩阵；l为li构成的含有观测信息的向量。

在最小二乘意义下，可解得未知数（坐标改正量）向量为：

在求得权阵P所对应的单位权方差估值后，即可获得点位坐标的方差阵：

值得说明，由于多余观测数通常较少，对于多个定位点，平差计算获得的单位权方差会缺少足够的稳定度，可根据多点定位结果综合估算观测量的单位权中误差。对于同类观测量，通常假定各观测量独立等精度，此时，平差过程所用的权阵即为单位阵，所综合求定的单位权方差为每个观测量的精度指标。

当求得点位方差阵后，可计算点位方差和点位中误差，并计算误差椭圆元素。而这种精度估计属于验后数据的内精度指标。而根据二位置线交会原理所估算的点位中误差及误差椭圆元素则主要用于定位方案制定。