海上运动载体的常规定位，主要是利用方位、距离、角度和距离差等形式的两个以上观测量，通过解析求解或等值线相交的交会模拟方法确定二维位置。所用的观测量可以是同一类型，也可以是不同类型的组合。

除中远程无线电定位系统主要采取双曲线定位模式，且需要基于地理坐标系之外，其他定位模式主要适用于运动载体与测量控制点配置较近的视距范围内的情形，因此直接采用投影平面坐标系。

1.前方交会定位

所采用的观测量为固定控制点向运动平台上的两个以上方位观测值，该交会方法的原理性实现如图4-7所示。

图4-7　前方交会示意图

在海上定位作业中，最传统的方法是根据控制点的配置情况，以适当密度绘制覆盖定位海区的方位等值线格网，根据测定的方位，由网格线内插技术确定运动载体的图上位置，此即前方交会的图解法。

点位的解析求解公式为：

该点位计算公式即变形戎格公式。公式的导出过程如下：

根据

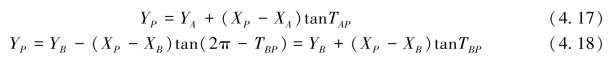
故

从而式（4.16）中计算XP的公式成立。

根据公式（4.17）和XP的推导结果，可推得由观测量和已知点坐标信息解算YP的公式。

值得说明，在固定控制点上，通过测角仪器测定已知点到待定流动点的方位的前方交会方法，采用公式（4.16）进行待定点点位计算，要求测站点A、待定点P和测站点B按顺时针顺序排列，否则公式形式会有所不同。

2.测角后方交会定位

测角后方交会定位，其原理与测量学中所述的技术方法并无本质区别，最大的技术性差异表现在三个方面。第一，与前方交会应用类似，陆地测量中的后方交会也通常要求有多余观测，即面对四个观测目标测定三个角度，而海上后方交会定位的主要模式是观测三个目标间的相邻角度。第二，采用的仪器设备不同，海上测角使用传统航海定位仪器是六分仪，观测设备不存在整平对中条件，不仅仪器的读数精度与陆地测量采用的经纬仪测角存在数量级的差异，所需的水平角观测也被空中的倾斜平面角所代替，只有当测点与照准目标间存在明显的高度差异时，才考虑倾斜平面角向水平角的改正，因此所测定的角度总体处于更低的精度等级。第三，在一般的导航定位中，采用与平板仪测图类似的模拟法定位手段，在海上即利用三杆分度仪确定待定点的图上位置，或绘制两组角度的等值线格网，根据观测值在格网上内插出测点位置。

利用后方交会法解析计算海上流动点位置的具体算法有多种，如计算辅助角，将解算问题变成测角前方交会问题的方法；又如坐标转换方法，在一般测量学文献中均有描述，在此略去具体计算方法和过程。(www.daowen.com)

根据后方交会角向水平面角的归算原理，后方交会定位的计算为迭代过程，即首先将观测的角度近似认为是水平角，应用后方交会定位的计算公式确定待定点P的近似坐标，进一步计算其到控制点的近似距离，并利用控制点的高程计算垂直角，进而实现观测角的归算，利用归算的角度，按交会定位公式重新精化确定待定点坐标。

3.侧方交会

因为侧方交会分别在一个已知（控制）点和待定点观测与相互目标点及与另一控制点之间的水平角，且在海上定位中，通常不存在多余观测，因此，除采用格网内插法模拟定位外，可转换为前方交会图形，利用前方交会原理解析计算待定点位置。

4.测距交会

采用测距模式获得一对观测量，除按格网内插法模拟（图解）确定测点位置外，可用以下距离交会解析公式确定待定点坐标。

假设二控制点分别标记为A、B，待定点记为P，且A、P、B依顺时针顺序排列，如图4-8所示，基于△ABP，待定点P的坐标计算公式为：

式中，TAB为控制点A、B的方位角；h为△ABP底边AB上的高；l为观测距离rAP在AB上的投影，且

式中，rAP、rBP为待定点P分别与控制点A、B的水平距离（实测距离的归算值）。

因为参与距离交会定位的观测量的等值线为两条（或以上）圆曲线，这种定位模式常称为圆-圆定位。

图4-8　测距交会解析计算原理示意图

5.方位距离定位

利用全站仪、经纬仪等测角测距组合模式的海上定位原理较为简单，通常情况下，将测角和测距仪器假设于沿岸或海岛控制点A，在通过相邻已知点确定测角仪器的度盘方向的情况下，可直接测定仪器所在的坐标已知的测站点至定位点P的方位TAP，由测距功能测定至目标点的直线距离，并根据垂直角，经归算获得水平距离rAP，则可直接根据坐标正算公式求得待定点坐标：

6.双曲线定位

双曲线定位是传统无线电定位的典型模式，由三个以上岸基无线电发射台和海上移动载体的无线电接收装置构成无线电定位系统。海上运动载体的电磁波接收和测定装置主要通过对来自两个岸基无线电台（岸台）发射的电磁波进行相位差测定，即可确定到所对应两个岸台的距离差。对两组相位差进行测定时，即获取通过定位所在点的两条双曲线，此时双曲线记为相位差或距离差观测量的等值线，两条双曲线的交点即定位点位置。

以双曲线形式进行海上导航定位的远程无线电定位系统具有无线电定位信号对大范围海洋覆盖的能力，通常要布设多个岸台，在海洋上的不同位置，根据信号强度和测点位置与岸台的几何配置条件选取两条定位位置线实施定位，但这类主要用于船舶导航的定位系统的电磁波信号在远距离传播过程中受到更显著的误差影响，一般而言定位精度较低。而专门用于测量定位的无线电系统主要采用略高频率的电磁波工作，尽管覆盖范围有所缩小，但可以保证更高的定位精度。此种类型的无线电定位系统即前文所述无线电大地测量定位系统。

无论是远程还是中近程无线电定位系统，在海上定位信号的覆盖范围相对前述传统的陆标测角（方位）、测距定位模式而言，都有极大的扩展，在一定的历史时期，反映出解决广阔海域定位问题的主导能力。有鉴于此，精度要求较高的双曲线定位解算都不能依据平面解析几何原理，而必须考虑地球表面的弯曲形态，依据椭球大地测量的基本算法，基于椭球形态的地球形状进行位置解算。当然，在一般的导航应用和测绘定位中，通常通过前期计算，将地球椭球面上的双曲线等值线计算结果变换至高斯投影平面或墨卡托投影平面，由图解法完成实时定位。

鉴于无线电定位的计算方法涉及一组繁冗的公式，特别是在椭球面上解算定位点位置，情况更为复杂。而在海洋大地测量定位中的应用日益减少，详细的定位原理在此不作介绍。