观测值不同的一组观测量构成位置函数的等值线。根据观测量类型的不同，位置函数（标量函数）等值线也对应地取不同形式。对于方位、角度、距离和距离差等不同观测量，分别存在射线、圆、双曲线等位置函数的等值线，简述如下。

1.方位观测量

在海洋测绘中，通常在已知控制点（大地控制点或海控点）上观测到海上运动载体的方位，获取控制点到定位点的方位观测量，一般由经纬仪测定。方位角则通过测站点与另一已知点的坐标值标定。方位观测量及其与控制点和待定点关系如图4-2所示。

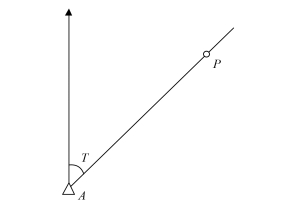
图4-2　控制点上的方位观测示意图

方位观测的函数表达式为：

式中，TAP为控制点A指向待定点P的方位（坐标方位角）；（XA，YA ）、（XP，YP ）分别为已知点和待定点的坐标。

2.角度观测量

在运动载体上向两个点位已知的控制点观测获得的角度，其等值线为所涉及三点的外接圆，随着待定点的位置变化，形成一簇对应不同角度量的圆形等值线。在二维平面坐标基面上，描述动态定位点与所照准的控制点、角度观测量以及其所在的等值线的关系如图4-3所示。

图4-3　角度观测量及其等值线

这种水平角通常用α表示，观测的函数表达式为：

上式中的角度应位于坐标解算平面或其平行面，从而保证是当地的水平面角，由方位差表示。而实际在动态载体上，角度一般由六分仪测定，所测定的角度为空间倾斜平面上的二直线的夹角β，如图4-4所示。

图4-4　倾斜平面角与水平面平面角的关系

根据图4-4，显然有：

其中，γ为测点对照准目标的高度角。于是有：

显然，倾斜平面上的观测角与其在水平面上的投影之间的差异与观测角度的大小有关，也与观测点到目标的垂直角有关。

如当观测角为30°，垂直角均为5°时，可算得α-β≈7′。因为用六分仪测角的估读分辨率为6′，所以在近岸高目标测量时，这种角度的化算是必要的。只有当观测点与待定点的距离较远，垂直角均较小时，可近似地认为测角平面近似与坐标平面重合。

3.距离观测量

在陆地控制点与运动平台之间，通过测距仪器和反射装置即可实现动态距离测量。自20世纪50年代后，光电技术的快速发展曾推动测距技术在海洋定位中的应用，与陆地测边网大地控制技术的发展基本处于同一时期。当然，海洋定位中的测距技术应用除需考虑距离测量技术本身之外，与角度和方位测量一样，还要考虑动态性，即测距仪器对反射装置的跟踪问题。早期曾发展微波动态测距技术和专用的仪器设备，后来无线电导航定位系统也应用于这种动态测距。而随着全站型经纬仪的技术成熟，在离岸较近的距离内，采用全站仪测定方位和距离的技术应用更为普遍，它的优势在于根据观测的垂直角，可直接将电磁波技术观测的斜距转换为水平距离。而由单纯的测距仪器给出的距离观测值，在离岸较近时，必要的情况下应考虑距离的水平归算。

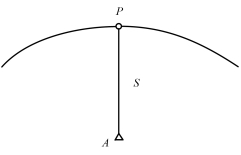
因为距离本身无方向性，无论将测距主要仪器置于运动平台还是固定控制点，距离观测量的等值线均为以固定点为圆心、观测距离为半径的圆弧。距离等值线及其与控制点的配置关系如图4-5所示。

距离观测量的函数形式为：

4.距离差观测量

全球导航卫星定位技术应用之前，在海上船只等平台定位的诸方法中，无线电导航系统发挥了极其重要的作用，与光学定位技术相比，它的显著优势在于提供超视距，特别是针对远距离定位观测量。

(www.daowen.com)

图4-5　距离等值线

在陆地（海岸或海岛）上两个固定控制点布设无线电岸台，若两个岸台同时发射的无线电信号分别经距离S0和S1传播被运动平台（统称船台）所接收，对这两个距离量求差值，则得到船台到两个岸台的距离差，距离差相等的点所形成的等值线为以两个岸台为焦点的双曲线。等值线的形式如图4-6所示。

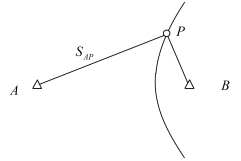
图4-6　距离差等值线

无线电导航定位系统按所提供的观测量类型，可分为测距系统和测距差系统，当然，测定的距离差是定位点与两个无线电信号发射台站点（岸台）距离的差值，因此最根本的观测量仍为距离。根据所发射的无线电信号特征，距离测量分别采用脉冲、相位和脉冲相位组合三种实现形式。而采用不同类型的距离观测方式，作用距离和达到的观测精度也有所不同。

脉冲式测距是通过测定无线电脉冲信号的收发时间差，即利用电磁波的传播时间，在已知电磁波传播速度的前提下测定距离。进一步通过测定一个接收台站与两个发射台站的电磁波传播时间差测定距离差。应用电磁波脉冲测定距离或距离差所能达到的精度主要决定于计时精度，也决定于电磁波的传播路径。采用脉冲测量模式测定距离差的典型无线电定位系统是罗兰-A，这种系统的无线电波在海面上传播的有效距离为600～900海里，系统的时间差测量误差为1～2μs，因此，距离差测定误差为300～600m。夜间，电磁波信号在海面的直接传播有效距离将降低到500海里左右，然而，电磁波在海面与电离层之间可能会发生反射，信号的作用距离可达到1200～1400海里，这种情况下，时间差的测定误差将增加到2～6μs，明显增大距离差的测定误差。除此之外，电磁波传播路径的归算及其误差也会影响距离差的测定误差。总体而言，依据脉冲测量距离差原理的远程无线电导航系统所提供的位置信息在历史上主要用于大洋航海定位，在海上测量任务实施方面，也曾经是重要技术。

基于相位测量模式，可以显著提高距离差的测定精度，也是采用距离差观测量实施海上中远程定位的主要原因。

这类导航定位系统的岸台连续发射固定频率的电磁波，电磁波的频率、周期和角速率之间满足如下关系：

式中，f为电磁波的频率；T为电磁波周期，即完成一次完整振荡的时间；ω为电磁振荡的角速率。

电磁振荡信号在空间中以信号发射的同频率传播，传播速度为光速c，并受到传播介质的影响。传播一个完整波形所用时间为波周期T，传播的距离为波长λ，期间波动相位的变化量为2π。传播一定距离完成的波形变化次数称为波数n。

由信号发射点A传播到接收点P，电磁波所行经的距离rAP可表示为：

该距离对应的相位变化量为δθ＝2nAP·π，即A点发射和P点接收的无线电信号可分别写为：

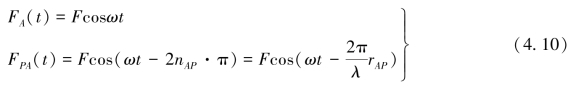
式中，F为电磁波的波幅。

若固定点B同样发射电磁波信号，且频率及发射相位与A点同步，则B点发射信号传播至接收点P时，所接收的信号表达为：

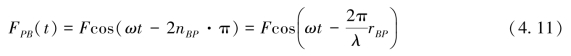
因此，通过在接收点P对所接收信号进行相位比对，所得相位差包含了距离差信息，即

以上诸式中，nAP和nBP表示从不同电磁波信号发射点到接收点电磁波传播的周期数，亦称为相位周数或波数；Δn表示两条电磁波传播路径的波数差。而不论波数或波数差都可分别为整波数和不足一周的小数两部分的组合，对于Δn，即有

式中，Δn1为波数差Δn的整数部分，而Δn2为不足一周的小数部分。

事实上，通过相位比较，直接得出的观测量为相位周的小数部分Δn2，整周差数Δn1作为未知数或模糊度需要通过其他手段测定或确定。比如，通过在已知点上观测和计算，对整周数赋值，并在测量过程中保持对无线电信号的连续跟踪，实现整周数的正确累加，或通过电磁波的分频技术确定基本测量波段的相位整周数。无线电波传播整周数或两条路径电磁波传播的波数差的确定方法总体上与陆地微波距离或距离差测量、载波作为观测量的精密导航卫星定位确定整周模糊度的原理相类似。

鉴于无线电测量距离差技术在历史上的重要性，总体而言在此仅作原理性说明，实际的导航定位系统的具体实现要复杂得多，还涉及无线电发射和接收台站的本振信号产生与同步，或由主发射台到副发射台的传播延迟修正（补偿）等技术，以及基频信号的生成与倍频和差频信号产生等复杂技术。而由相位差或相位波数之差转换为距离差还涉及电磁波传播速度的精确测定等技术问题。

无论如何，由无线电测量技术获得流动站点到两个固定站点的距离差，通常采用的无线电波为长波，以保证传播路径沿地球表面（海面）最短路径传播，而不能用过高频率的电磁波，以免更易以接近直线的传播形式使得定位载体与固定陆地之间无法获取相关观测量，失去定位条件。在电磁波速度已知、信号产生的同步性得以保证以及整周未知数正确确定的前提下，距离差的测定精度主要取决于相位周小数部分的比测精度，因为相位周小数以对相位周（波长）的划分代替了对角度周期2π的划分。相位周的测定精度实际上可由波长测定的相对误差来表达。对于长波无线电信号，波长通常为数百米，相位周的测定精度基本可达到波长的10-3～10-2。因此，相位模式的相位差测量，等价距离差测量，精度可达数米到数十米精度量级，相对于脉冲测距差方式，可极大改善脉冲模式测定距离差的精度。

典型的无线电导航系统中，“罗兰-C”系统采用脉冲-相位两种测量方式，显然脉冲方式可为相位测量方式提供必要的整周未知数确定的参考信息。除此之外，“台卡”系统、“奥米加”系统都是采用相位模式进行距离差测定的典型无线电导航系统。这些系统设计和运行的目标主要是保证船舶的导航定位，在海上有关测量定位中，也曾是经常用于位置服务的主要技术手段。

为了满足更高精度的海上测量定位需要，曾经研制和应用主要服务于海上测量定位的无线电系统，在国外曾被称为无线电大地测量的距离差系统。这种系统除定位精度较导航系统高之外，岸台也通常根据测量任务需求，灵活布设于已知的大地测量控制点（以及海控点）。而高精度距离差的测定，主要采用波长略短的无线电波（作用范围与位置服务区域相适应），并通过布设检查台提供位置的差分订正信号。主要的系统有：“巴依斯克”系统、“哈-菲克斯”系统、“西-菲克斯”系统。我国曾使用“近程无线电IV型导航系统”。

因为测量原理相近，也曾存在根据无线电测相定位模式的距离测量系统。在平面坐标系中，距离差观测的函数形式为：