声源是声场产生的重要条件，声源辐射能量形成声场。点声源辐射的声波无方向性。无论依据何种物理原理制作的水声换能器，均设计为一定的形状和尺寸，因此，实际应用的换能器不是也不能视为点声源，但可以将其看作是由无数点声源组合而成。根据波的干涉原理，由多声源发出的声波传播至空间某一点时，将形成波（振动）的合成，合成的效果是在不同的方向上，波的能量不同，可以使声能主要聚集在某一设定的角度范围内，这种现象就是换能器的方向特性，即指向性（Directivity），它是在海底地形测量中有效和合理使用换能器的重要指标参数。因为通过设计，可使得换能器对所需的探测方向声能增强，从而增强在特定方向的测量距离，同时，接收回波也有一定的方向性，从而提高测定目标方向的准确性。此外，发射和接收均具有方向性，可以避免探测方向之外的噪声干扰，提高探测的抗干扰能力和目标识别的灵敏度。

1.声波方向性的形成原理

一个无指向性的声脉冲在水中发射后，以球形等幅度远离发射源传播，所以各方向上的声能相等。这种均匀传播称为等方向性传播（Isotropic Expansion），发射阵也叫等方向性源（Isotropic Source）。当向平静的水面扔入一颗小石头时，就会产生这种类似波形，如图3-14所示。

因为这种声波是等方向性传播，没有固定的指向性，所以在海底测深时不能使用这种声波，必须利用发射基阵使声波指向特定的方向。在了解指向性之前，首先介绍声波的相长干涉和相消干涉。

当两个相邻的发射器发射相同的各向同性的声信号时，声波将互相重叠或干涉，如图3-15所示。两个波峰或两个波谷之间的叠加会增强波的能量，这种叠加增强的现象称为相长干涉；波峰与波谷的叠加正好互相抵消，能量为零，这种互相抵消的现象称为相消干涉。一般地，相长干涉发生在距离每个发射器相等的点或者整波长处，而相消干涉发生在相距发射器半波长或者整波长加半波长处。显然，水听器需要放置在相长干涉处（阳凡林，2003）。

图3-14　声波的等方向性传播

图3-15　声波的干涉

如换能器声基元间距d（图3-15中1、2点的距离）是λ/2（半波长），此时，相长干涉发生在θ＝0°和θ＝180°的位置；相消干涉发生在θ＝90°和θ＝270°的位置，如图3-16所示。

设有两个产生声压幅值和位相均相等的点声源S1、S2，二者间的距离为d，连线的中点记为O。远场空间任一点M至S1、S2和O点的距离分别为r1、r2和r，如图3-17所示。

点声源S1和S2均发射p＝pmcosωt的声信号，声压传播到M点时的声压p1和p2分别为：

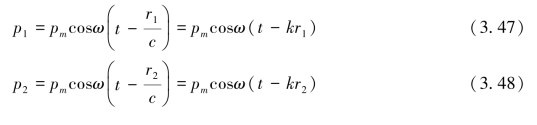
其中，

图3-16　两个发射器相距λ/2时的相长和相消干涉

图3-17　双点声源

根据波的叠加原理，在M点的合成声压为：

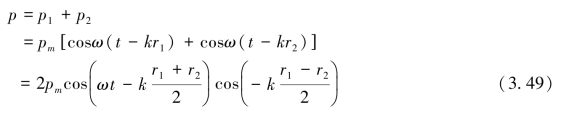
因为M为远场点，r＞＞d，可近似认为声线r1、r2近似平行，则有在此Δr＝r1-r2≈dsinθ，为所研究点的波程差。因此，M点的合成声压可改写为：

由此可见，经过声波合成，合成声压的幅值pm0（θ）随角度θ而变，即合成声波是空间中的变幅波动。θ为双点声源的中垂线ON与OM线的夹角。

当即波程差时，合成声压取极大值。也就是说当波程差为半波长的偶数倍时，合成声压因波的同相叠加而增强。

当即波程差时，合成声压取极小值为p＝0。也就是说波程差为半波长的奇数倍时，两声波在合成过程中总因位相相反而相互抵消。

这样，在θ＝0°处，有最大声压幅值2pm，在其他方向上，0＜sinθ＜1，合成声压幅值比θ＝0°方向的声压小，从而形成了声波辐射时的方向特性。

2.均匀线列阵与直线型换能器的方向性

均匀线列阵是由若干个灵敏度均匀、振动、相位一致，振幅相同的换能器基元（如复合棒型换能器）排列在一条直线上形成的。基元的直径远小于波长，所以单个基元是无指向性的基元依间距d在直线上等距排列。

换能器产生方向性的原因是非点源换能器上各点所发出的声波到达远离场源空间某点的时间不同，存在相位差（即波程差），如图3-18所示，在空间一点的合成声波幅值将是夹角θ的函数。

图3-18　均匀线列阵

对于偏离法线θ角方向上的远场M1点，相邻两个基元发射声波的波程差为dsinθ，即以0号基元为参考，从1号到N-1号基元发射的声波到M1点波程差分别为n·dsinθ，其中n＝1，2，…，N-1。

各基元发射声波传递至M1时，辐射声压表示为整个线列基元阵在M1产生的声压是各基元作用的合成：

显然，求和部分为等比数列，根据等比数列求和公式有：

顾及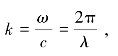线列阵声源在远场的声压主要依赖于目标点与线列阵法线方向的夹角θ，忽略声能的传播损失，顾及远场条件，将r1改写为距线列阵中点的距离r，同时顾及于是合成声压表示为：

当θ＝0时，即探测点在线列阵的中垂线方向时，据罗必塔法则，易知

若基元间距无限减小，即当d→0，N→∞，且Nd＝L时，则取式（3.39）的极限形式：

式（3.55）为连续直线（线段）声源的声压合成公式。此式还可以通过对双点源合成声压公式的积分导出。

根据罗必塔法则，同样可以求得：

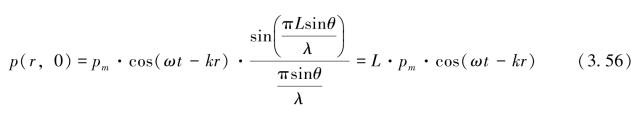
3.均匀线列阵与直线型声源的声波发射指向性参数

不论是均匀线列阵，还是直线型连续声源，在远场的声波为变振幅波动，声压均与声波的辐射角θ密切相关。将变化声压的幅值系数记为Pm0（θ），显然，对于均匀线列阵和直线型声源，声压幅值系数分别为：

式（3.57）和式（3.58）中，等式右端的余弦项使得声压幅值将随着θ由0°向±90°变化而减小（绝对值），故一般予以忽略，则以上二式可分别简化为：

合成声压的幅值将在正、负之间振荡变化，因为声压的宏观作用主要于有效声压（瞬时声压对时间的均方根值），故在实际问题分析中，式（3.59）和式（3.60）总是取绝对值，而将振幅在正负值之间的变化归于声波相位的变化。

前述分析已经发现，振幅系数的最大值将出现在θ＝0的方向。故定义任意方向的振幅与最大振幅方向振幅的比值（绝对值）为声源的方向特性函数，记为G（θ），即

据此，可导得均匀线列阵和直线型声源的方向特性函数分别为：

方向性指向函数以“1”为最大值，出现在θ＝0的方向上。随着指向角向正、负两个方向增大，通过对声压振幅公式求导，尽管也可得若干极大值点，但在这些方向上，指向性函数值会迅速衰减。对于连续线性声源，这些极大值对应的方向角满足条件：

即

将G（θ）＝1时，称为主极大，波束能量最强，声波能量形成的波瓣称为主波瓣，而其他极大值称为副极大，产生的波瓣为副波瓣或旁向波瓣（旁瓣）。

根据式（3.63），当n＝0，对应的方向即主极大，θ0＝0°，G（θ0）＝1。而n取其他数值时，

当方向特性函数G（θ）＝0时，称为极小值。极小值对应的θ角满足：

具体的θ角值为：

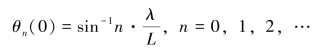
由于方向特性函数G（θ）为连续函数，故极大与极小值之间会交替变化，故形成前述的声波波瓣效应。

波瓣中心与相邻的极小值点（零点）的角距定义为方向性锐度角，主极大两侧第一个极小值（对应角点）之间的夹角记为Θ，即

它的含义是主波瓣的宽度。

因此，当换能器长度L的值越大，声波的频率越高（波长越小，决定于换能器本身的振动频率），则方向性锐角越小，声波的指向性越好。

取换能器长度为所发射声波波长的整倍数，即L＝mλ，相应的方向性锐角度列为表3-2。

表3-2　方向性锐角度随L/λ的变化

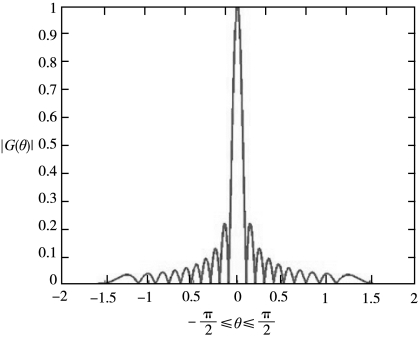
线型换能器的指向性函数曲线（L/λ＝10）如图3-19所示。

(www.daowen.com)

图3-19　连续线型声源指向性函数曲线

方向性锐角度可用于描述整个主波瓣的形状，而在应用中以一个与声波能量有关的量描述主瓣波束角（beam width of main-lobe），记为ΘW。具体定义为主瓣内声强为最大声强一半的点所夹的角度，即法线两侧半功率点之间所夹的角度，认为在此角之外的声能量就比较小了。

因为声强与声压幅值的平方成正比，则波束角边缘的声强与极大值声强的比值即声压幅值的平方比值，可直接利用指向性函数，根据波束角定义，有

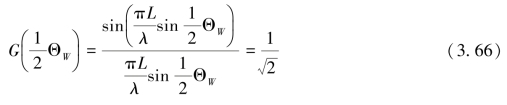
解此超越方程得：

（注：多数文献根据幂级数展开法，近似计算得此值为1.24。）

故

仍取换能器长度为所发射声波波长的整倍数，即L＝mλ，相应的主瓣波束角列为表3-3。

表3-3　主瓣波束角随L/λ的变化

而国际上，将主瓣波束角常定义为声强级为-3dB的点所夹的角（最大声强为0dB），如图3-20所示。

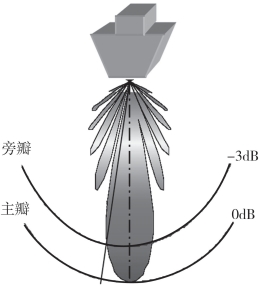
图3-20　由-3dB定义的主瓣波束角

据定义有：

所以，所确定的波束角与根据半功率点计算的结果基本一致。

4.典型平面形状换能器的发射声波指向性

均匀线列阵声源和均匀连续线型声源均表现为数学意义上的换能器，其声波指向性的分析仅限于沿声源轴向的方向特性，而环绕换能器轴，声波的指向是均匀的。实际换能器均设计为一定的平面或立体尺寸，可以对发射声波进行纵、横两个自由度的方向约束，更加明确发射声波的指向性。本部分主要分析矩形和圆形两种平面形态换能器的指向性及相关参数指标。

将线型换能器扩展至一定宽度，则形成矩形换能器，显然随着宽度增加，在原线型声源的垂直方向，也会限定声压的指向。

将矩形换能器的长度仍记为L，而短边记为D，对应的方向分别记为θL和θD，则其长边和短边方向的方向性指向函数分别为：

两个方向的方向性锐度角和主瓣波束角分别为：

由以上波束角的计算公式，所得的波束角以弧度为单位。通常需要用以“度”为单位表示。此时，而通常换能器的尺寸远大于声波波长，故对反正弦函数做幂级数展开，并取至一次项，有：

式（3.74）为估算线型连续声源或矩形换能器沿两个边缘方向波束角的估算公式。

在此以分析国产SDH-3型测深仪的有关波束参数为例。该型测深仪的换能器根据磁致伸缩原理工作，其几何尺寸为L·D＝16×9cm2，工作频率为f＝29.3kHz，设计声速取c＝1500m/s，从而设计的发射声波波长为λ＝c/f＝5.12cm。经计算：

纵向（长边方向）的方向性锐度角为：

波束角为：

半面极小值数为：[16/5.12]＝3，所以旁瓣数为2。

横向（短边方向）的方向性锐度角为：

极小值数为[9/5.12]＝1，无旁瓣；

波束角为：

半径为a的无限障板中的圆形声波辐射器如图3-21所示。所谓无限障板是指尺寸比辐射器的尺寸大得多，刚性很强的挡板，辐射器只有一面与介质接触，从而单面辐射声波，且辐射面上各点的振动完全相同。圆形辐射面中心为O，OZ为辐射面外法线。

由于圆平面的对称性，显然，在OZ方向线上产生最大合成声强。合成声压幅值的极大值为：pm0（0）＝pm·πa2。

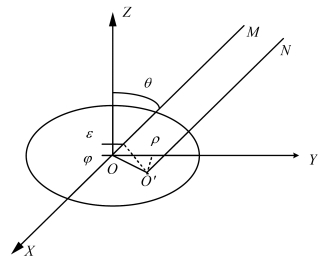
图3-21　无限障板中的圆形换能器（辐射器）

研究偏离法线θ角方向上的任一远场点M的声强，不妨设M点的球坐标为M（r，θ，0），取圆平面辐射器上的一流动点Q，极坐标为（ρ，φ），即球坐标为

可近似认为OM//QM，O点和Q点发射声波至M点的波程差为：ε＝ρsinθcosφ。

于是，两束声波在M点的相位差为：

声压的合成振幅仍以复数形式表示为：

该式的积分结果由第一类一阶贝塞尔函数表示，即

式中，d为圆辐射面的直径。

指向性函数为：

指向性函数的图像如图3-22所示（IHO，2005）。

当时，G（θ）第一次为零，由此得：所以方向性锐度角为：

图3-22　无限障板中的圆形换能器的指向性函数图像

而主瓣波束角为：

5.换能器的轴向聚集系数

在换能器的轴向方向上，声能将达到最大。然而，换能器发射的声波是具有指向性的。因此定义在原理换能器的某一距离上，主极大方向的声强Imax与相同功率无方向性的点声源在同一距离上所形成的声强I0之比为该换能器的轴向聚集系数，记为γ0，即

它的含义可理解为：在声场中同一距离上，为了获得相同的声强，具有方向性的换能器将比无方向性的点声源发射的功率减少γ0倍。在前述声波振幅和声压推导中，实际上忽略了这一系数，即未顾及声能传播的衰减，如图3-23所示（IHO，2005）。

轴向聚集系数和方向性函数均为描述换能器方向性的重要物理量，为此可导出二者的关系：

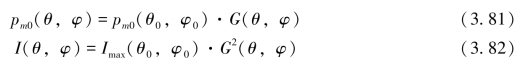
在距声源中心距离为r的球面上，声功率为：

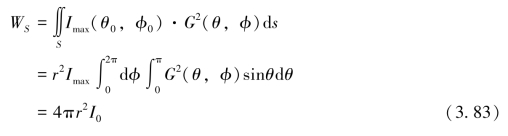
故

图3-23　声波指向性与无指向性的比较

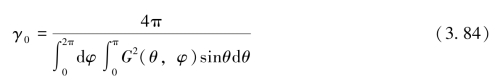
在换能器声轴对称的情况下，例如圆平面换能器的情形，有

而矩形平面换能器的轴向聚集系数为：

对于直线型连续声源，同样有轴向聚集系数：

定义轴向聚集系数常用对数的10倍为声波指向性指标，记为DI，显然，其单位为分贝，即

发射换能器具有方向特性，可以将声波能量集中在所需要的方向上，从而增加了声波探测的有效作用距离。