声速在介质中的传播性质采用声波波动方程来描述。波动方程的解有两种理论，一种是简正波理论，另一种是射线理论。简正波理论对于声速的波动现象如频散、影区绕射等解释较好，但计算方法过于繁琐。射线理论是一种近似处理方法，仅是高频条件下波动方程的近似解，但是在许多情况下，能够有效和直观解决海洋中的声传播问题，射线声学中用声线表示声波，类似于在光学中用光线表示光波。在此，结合这两种理论分别解释声信号的折射、散射和绕射规律，其中射线声学理论主要用于解释折射和反射现象。

1.声波的折射

根据基本的物理学原理，当声波传播至不同介质的界面时会发生折射现象。而水体，特别是海洋水体中，水介质的密度随同压力、温度和盐度具有连续变化，且主要呈现出垂向梯度变化，因此，可以在微分的意义上对水体进行水平分层，而声波在海水中倾斜传播时，同样会具有折射现象。这种现象由斯奈尔（Snell）定律来描述：

式中，θ1和θ2分别为声波与界面法线的夹角，即入射角和折射角；c1和c2为界面两侧的声速。该定律表明，因介质密度和其他参数引起的声速变化引起声线（声传播路径）与介质界面法线方向差异的变化，且这种角度的正弦比等于界面两侧的声速比。

当c1＞c2，即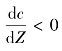（定义Z向下为正）时，θ1＞θ2，折射后声线向法线靠近；反之相反，即折射后声线远离法线，也就是说折射线总是向声速小的水层靠拢。

声波折射规律的示意图见图3-4。

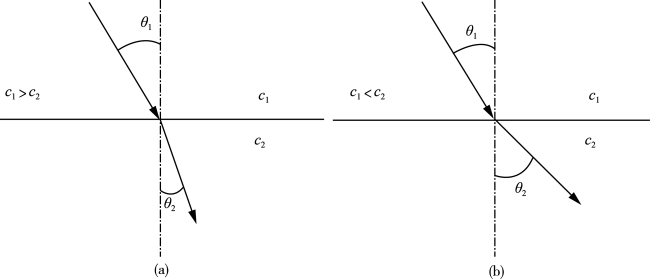
图3-4　声波在介质水平界面折射规律

在连续介质中，声速随深度的连续变化决定了声线方向的连续变化，从而造成声线传播的弯曲，也称为声波的曲射。根据声速梯度的不同，可以将声波在水中的传播路径，即声线的弯曲情况归结为以下三种典型情形。

（1）等速层中的声传播

声速的梯度此时声速不随深度变化。因此，声波在任意方向直线传播，声线的方向等同于入射角的方向。这种情况下的声速梯度和声线示意图见图3-5。

在绝对的等速层中声波按直线传播，对于水中距离测量是极其理想的状态。当然，绝对的等速层实际是少见的。由于声速的变化主要依赖于水中温度的变化，在充分混合均匀的海洋表层，可形成等温、等盐层，忽略静压力随深度变化对声速的影响，才近似出现这种情况。等温层的厚度有时可达数十米。

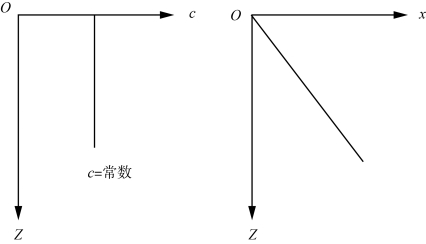
图3-5　等速层的声速梯度及声线

（2）负梯度层的声传播

声速的梯度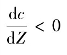的水层为负梯度层，根据Snell定律，在这样的水层，声波在以一定方向向下传播时，声线形成向垂线方向的弯曲，声速梯度（常梯度）和相应的声线弯曲情况如图3-6所示。

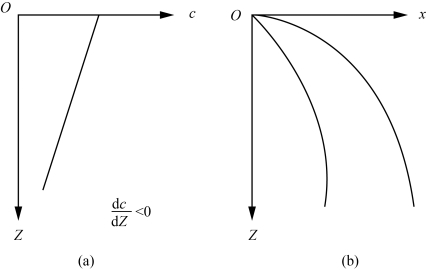
图3-6　负梯度层的声速梯度及声线

由于温度是声速的主要影响因素，且声速会随着温度的降低而减小，因此，在海洋区域，特别是温带和亚热带海域，因为对太阳能吸收程度的不同，海水的温度会随着深度的增加而降低，浅水层（数十米到百米量级的范围内）主要呈现声速的负梯度变化特征。

（3）正梯度层的声传播

声速的梯度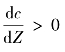的水层为正梯度层，与负梯度层的声波传播规律相反，声波以一定方向向下传播时声线向水平面方向弯曲，此时，声速梯度（常梯度）和相应的声线弯曲情况如图3-7所示。

(www.daowen.com)

图3-7　正梯度层的声速梯度及声线

在浅水层，因海气相互作用，冬季往往上层海水温度低。而随着深度的降低，水温略有升高，呈正梯度变化。而当声波达到一定的海洋深度，声速往往发生正梯度变化，这是因为在一定的深水层，温度基本达到守恒状态，对声速的主要影响来源于静压力增大引起的传播速度加快，也会存在正梯度现象。

为探索基本规律，以上分析仅就声速的常梯度变化讨论。在真实海洋及其他水域，由于温度、压力和盐度等影响声速的因素受到各种作用和扰动，使得声速梯度产生复杂的变化，声线会呈现出更为复杂的形态。这种连续的声速与声线变化如图3-8所示，在海底地形的多波束测量手段中，必须实施声速的现场精确测量，主要是基于多普勒原理的声速剖面测量，根据声速的变化，进行准确的声线跟踪，确定声线所探测海底点的三维位置。

在极值情况下，声线产生连续变形曲射，在其传播路径上会出现声速正、负梯度交替的现象，且声能损失小，因此形成声道，可传播远达数千公里的距离。但这种现象为海洋中的远程声学通信提供了可能，而不适于本书所关心的海底地形测量应用需求。

2.声波的散射

就水下地形测量而言，声测距的主要目的是实现对水底点的定位，因此，需要研究和讨论声波在水底和相应特征物界面的反射情况。

对于绝对平坦的水底（海底），声波会在这样的界面上产生镜反射。根据斯奈尔反射定律，以界面法线度量的入射角与反射角相等且对称，镜反射保证平行的入射声线反射为平行的反射声线。一般而言，由于海底物质不同、粒度不同以及不同尺度特征物的存在，使得界面的法线不平行，声波在这类海底则发生漫发射，称为散射。当然，就每条声线而言，仍遵从反射定律。

用几何尺度参数δ表示水底的粗糙度，当δ＝0时，出现严格意义上的镜反射。而当δ＜＜λ时，海底对声波的镜反射能力几乎不受影响，如图3-9所示。当δ增大至与声波波长λ相比尺度接近时，入射声波的散射程度增强，甚至无法形成一束比较集中的回波波束，如图3-10所示。

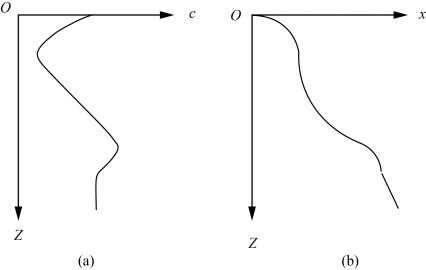
图3-8　声速和声线的连续变化示意图

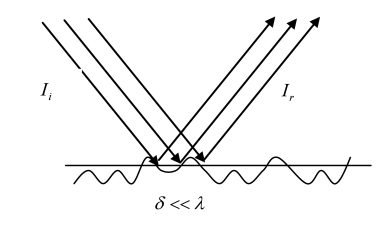
图3-9　近似的镜反射

其中沿入射波相反方向的散射称为反向散射，反向散射是倾斜测距原理有效实施测量所需的回波。显然，不同的海底底质，海底粗糙程度，入射声波的掠射角及声波的频率都将影响声波的散射。

正是声波的散射现象为海底的声探测提供了接收反射回波的条件。

3.声波的绕射

声波在传播路径上遇到尺寸有限的障碍物时，在存在反射现象的同时，会产生声波绕过障碍物的现象，即绕射现象。声波的绕射能力取决于障碍物尺寸和声波的波长，即决定于障碍物尺寸与声波波长的比值。如果障碍物的尺寸与声波波长的比值越小，则绕射现象越明显，即障碍物对声波传播的影响越小。刚性球不同半径时的声强反射系数如表3-1所示。

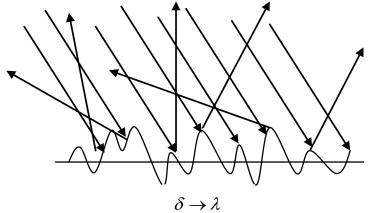
图3-10　声波的散射（漫反射）

表3-1　反射系数与水中目标尺寸的关系

从表3-1可见，刚性球尺寸相对波长λ越小，声强rI反射系数越小，声波大部分绕其而过，造成水声仪器探测不到小目标。对于固定尺寸障碍物，低频声波，即波长较长的声波容易发生绕射现象；而高频声波则不易绕过。所以，为探测小目标，必须采用高频声波。如探测直径约一米的水雷，工作频率至少在40kHz以上，甚至达到500kHz，相应的波长小于3.75cm。为了高分辨率地探测海底地形，高分辨率侧扫声呐的工作频率亦达100kHz。