声波表达式实际上是声波应满足的物理规律，即数学物理方程的解。根据数学物理方程基本理论，一维波动方程的一般形式为：

该方程可推导如下：

1.运动方程

在声场中取一小体积元，其横截面积为S，长度为dx，如图3-2所示。

图3-2　介质单元的声传播结构示意图

声在传播过程中，声压p随位置x而变化，显然，介质被压缩的部分声压大，而舒张部分的压力小。故体积元（以下简称“体元”）左右两侧所受声的作用力不相等，合力使得体积元沿x轴由压力大到压力小的方向运动。设体元左侧压强为p0+p，受力为F1＝（p0+p）·S，右侧压强和受力分别为p0+p+dp和（p0+p+dp）·S，其中声压增量为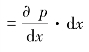，则体元的综合受力为：

顾及体元质量ρ·S·dx（ρ为介质密度），加速度描述为（其中，v为质点振动速度，注意并非声速），则根据牛顿第二运动定律有

即

当然，在此体元的加速度应分解为：

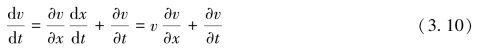
式（3.10）中，右端第一项的含义是由于介质在压缩和舒张状态下的不均匀性，质点运动速度随距离的变化率，而第二项为声速随时间的变化率。第一项实际为二阶向量，忽略时，运动方程为：

2.连续方程

连续方程实质上是介质质量守恒定律的数学表达式。在流体介质中，单位时间内流入与流出体积元的质量差为净质量的增加或减少。根据图3-2，单位时间内自左侧流入介质的质量为ρ·v·S，而从右侧流出的质量为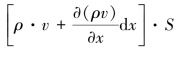，则介质质量的增量为因此，

连续方程描述了介质质点振速v与介质密度及其变化量之间的关系。

3.物态方程

在没有声扰动时，介质内某小体积元的物理状态可以用静态压强p0、密度ρ0、温度T0描述。当介质存在声波时，介质质点发生了压缩、膨胀的交替变化。这种介质状态的变化可由热力学状态方程描述。对于绝热过程，可认为压强p仅是密度ρ的函数p＝p（ρ）。由声扰动所引起的压强p和密度ρ的微小增量满足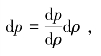由于dp与dρ的变化趋势相同，故总有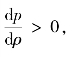不妨定义

在声学理论中，可以证明该式中的参数c为声波在特定介质（密度ρ）中的传播速度，即声速。

记p′＝p-p0为声压相对静态声压p0的变化量，同样ρ′＝ρ-ρ0为密度相对静态密度的变化量，则声压可由Taylor级数展开表示为：

式中，下标S表示等熵过程；c0是小信号（压力和密度的变化与其静态值比较均非常小）的声速；

在忽略二阶以上项时，式（3.14）简化为：

4.声波方程

考虑密度变化为小信号变化，在式（3.12）中，将ρv改写为ρ0v，并将式（3.15）代入式（3.12）中，得：

进一步对时间变量t求导，得：

式（3.11）进一步对空间变量x求导，得：

组合式（3.17）和式（3.18），有：

(www.daowen.com)

考虑到密度和压力仅存在小幅变化，从而静态介质中的声速可代换为变化声速，即可改写为c2，则由式（3.7）所描述的声波方程是数学物理方程中所研究的通用形式的波动方程。当然，该方程是在忽略了二阶以上微小量后得到的，为线性声波波动方程，有其赖以成立的前提条件。

将声场的范围由一维空间扩展至三维空间，可得到无限空间中各向同性理想流体介质中的球面波的波动方程：

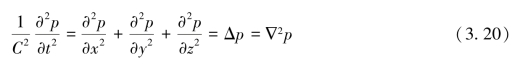
其中，为Laplace算子。

5.声波方程的解

根据数学物理方程基本理论，式（3.19）所表达的一维声波方程的解为：

其中，f1和f2是任意函数，而这成为波动方程解的条件是它们具有一阶和二阶导数且连续。将式（3.21）代入式（3.19），不难验证满足该声波方程。由f1（x-c0t）可见，当xc0t为常数时，函数值f1（x-c0t）为不变；特别是当x-c0t＝0时，表明x0＝0的函数向x方向移动c0t，即f1（x-c0t）为向x正向传播的声波，而第二项则表示反向传播的声波。根据物理意义及应用，一般仅关注正向声波。以后将进一步说明，若将x方向作为直角坐标系的一个轴向，这种沿一维的声波即为平面波。

将正向波代入运动方程，则有：

为f1对时间t的导数，对时间积分得：

从而，介质运动速率为：

式中，Z0称为介质的特性阻抗，是介质的固有属性，与波形和频率无关；在水中，c0≈1500m/s，ρ0≈1000kg/m3。

根据Fourier分析的基本理论，任何时间函数f（t）都可分解为简谐项之和，因此，稳定函数（波形）都可通过Fourier分量求得其特性，特别是在本书的研究体系中，所考虑的都是固定频率的声波。正向传播的声波通常写为：

式中的相关参数已在3.1.1中描述，只是在此需要进一步明确

为了对声压（以及质点速度）等声场主要场量的分析计算方便，常常采用复数表示法，即将式（3.25）改写为：

因为所研究的场量为实数，在运算过程中，往往省略取实部符号，其意义仍理解为在计算后，采用实部的推演结果。

研究三维空间中的波动问题，首先要对声波方程（3.20）求解，而方程的求解一般利用球坐标系。

球坐标（r，θ，φ）与空间直角坐标（x，y，z）之间的关系见图3-3，相互转换式为：

图3-3　球面坐标系与空间直角坐标系

在球坐标系下，拉普拉斯算子变形为：

这类数学物理方程求解的常用方法之一是分离变量法，其基本思想是将场函数（如声学问题中的声压场p（r，θ，φ，t））描述为空间变量时变函数的乘积，代入方程，根据初值条件和边值条件求解。

在球坐标系下，将声源置于坐标系的原点，则对于均匀声介质，声源振动产生的声波向空中传递，时间参量仅与距离有关，因此，可将声压分解为如下形式：

对于点声源，显然其产生的声场向周边均匀介质辐射与方向无关，因此，拉普拉斯算子中只需解关于r的部分

波动方程在分离变量后变为

其中，k2是分离变量过程中引入的积分常数，而对于简谐波，而方程的形式解为：

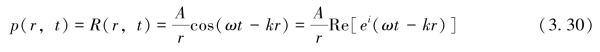
与平面声波具有等同的形式。

点声源是一种理想化的声源模型，而实际应用中，声源均具有某种对称的几何形状，产生的声波也具有对称性，一般考虑与φ无关，即关于θ对称，其解的形式即取