1）运动微分方程的建立

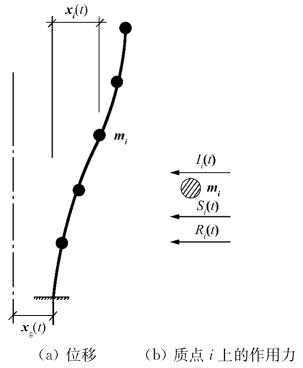
图3-9　多质点弹性体系变形

在单向水平地震作用下，忽略扭转的影响，此时n个质点的结构体系有n个自由度。图3-9为多自由度弹性体系在水平地震作用下的位移情况。图中xg（t）为地震时地面运动的水平位移；xi（t）表示i质点相对于地面的相对弹性水平位移。这时，作用在图3-9中质点i上的力有：

惯性力

弹性恢复力

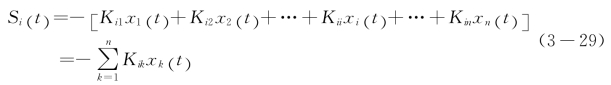
阻尼力

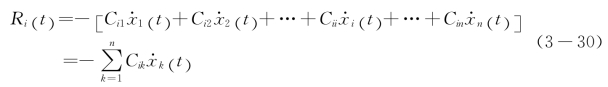
式中：Ii（t）、Si（t）、Ri（t）——分别为作用于质点i上的惯性力、弹性恢复力和阻尼力；

Kik——质点k处产生单位侧移，其他质点保持不动，在质点i处引起的弹性反力；

Cik——质点k处产生单位速度，其他质点保持不动，在质点i处产生的阻尼力；

mi——集中在质点i上的集中质量；

xi（t）、——分别为质点i的相对侧移、相对速度和相对加速度。

根据达伦倍尔（D'Alembert）原理，质点i在上述3个力作用下处于平衡，即

将式（3-28）、（3-29）、（3-30）代入式（3-31），则有

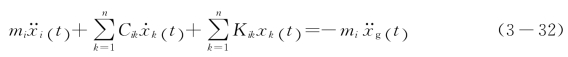
对于n质点的弹性体系，有n个类似于式（3-32）的方程，这n个方程的矩阵表达式为

式中：［M］——质量矩阵，是一个对角矩阵；

［K］——刚度矩阵，即除主对角线和两个副对角线外，其余元素均为零；

［C］——阻尼矩阵。

2）多自由度弹性体系的自由振动

（1）主振型

将式（3-33）中的阻尼项和右端项略去，即可得到无阻尼多自由度弹性体系的自由振动方程

设方程的解为

式中：——体系的振动幅值向量；

φ——初相角。

将式（3-35）代入式（3-34），得

式（3-36）是体系的振动幅值的齐次方程，称为特征方程。为了得到的非零解，系数行列式必须等于零，即

将行列式展开，可得到一个关于频率参数ω2的n次代数方程。求出这个方程的n个根（特征值），即可得出体系的n个自振频率。由n个ω值可以求得n个自振周期T，将n个自振周期T由大到小的顺序进行排列：

T1＞T2＞…＞Tj…＞Tn

其中最大的周期T1称为第一周期或基本周期，与T1对应的最小频率ω1称为第一频率或基本频率。

将求得的ωj依次回代到方程（3-37），可以求得对应于每一频率值时体系各质点的相对振幅，用这些相对振幅值绘制的体系各质点的侧移曲线就是对应于该频率的主振型，简称振型。其中与基本周期T1对应的第一振型称为基本振型，其他各振型统称为高振型。(www.daowen.com)

（2）主振型的正交性

多自由度弹性体系做自由振动时，任意两个不同频率的主振型间都存在正交性。利用振型的正交性原理可以大大简化多自由度弹性体系运动微分方程的求解。

①振型关于质量矩阵的正交性

其矩阵表达式为

它说明：某一振型在振动过程中所引起的惯性力不在其他振型上做功，体系按某一振型做自由振动时不会激起该体系其他振型的振动。

②振型关于刚度矩阵的正交性

其矩阵表达式为

它说明：体系按k振型振动引起的弹性恢复力在j振型位移所做的功之和等于零，也即体系按某一振型振动时，它的位移不会转移到其他振型上去。

③振型关于阻尼矩阵的正交性

其矩阵表达式为

3）运动微分方程的解

多自由度弹性体系在单向水平地震作用下的运动方程为一相互耦联的微分方程组，要利用振型分解法来求解。振型分解法就是利用各振型相互正交的特性，将原来耦联的微分方程组变为若干互相独立的微分方程，从而使原来多自由度体系的动力计算变为若干个单自由度体系的问题，在求得了各单自由度体系的解后，再将各个解进行组合，从而可求得多自由度体系的地震反应。

根据振型叠加原理，弹性结构体系中任一质点在振动过程中的侧移xi（t）可以表示为

式中qj（t）为j振型的广义坐标，是时间t的函数。整个体系的位移列向量、速度列向量和加速度列向量都可以按振型分解用qj（t）表达。

将位移列向量、速度列向量和加速度列向量的振型分解表达式，代入多自由度弹性体系有阻尼运动方程（3-32），并利用振型的正交性对方程进行简化，展开后可得n个独立的二阶微分方程，对于第j振型可写为

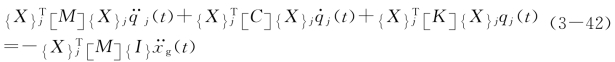
再引入广义质量、广义刚度和广义阻尼的符号，得

广义质量、广义刚度和广义阻尼的表达式为

广义质量、广义刚度和广义阻尼有下列关系：

将式（3-45）代入式（3-44），并用j振型的广义质量除等式两端，得

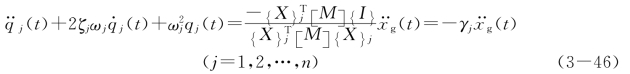
式（3-46）中的γj称为j振型的振型参与系数，即

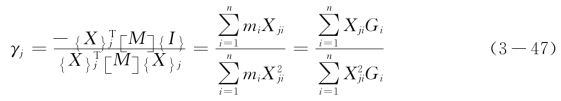
它满足。

式中：Gi——i质点的重力荷载代表值；

Xji——第j振型在i质点的振幅。

式（3-46）相当于一个单自由度弹性体系的运动方程，未知量为广义坐标qj（t），其解为

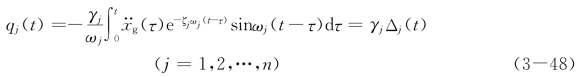
求得各振型的广义坐标qj（t）后，就可按式（3-41）求出原体系i质点相对于地面的侧移反应和相对加速度反应：

利用振型分解法不仅对计算多质点体系的地震位移反应十分简便，而且也为按反应谱理论计算多质点体系的地震作用提供了方便。工程结构抗震设计最关心的是各质点地震反应的最大值，对自由度弹性体系，在振型分解法的基础上，结合单自由度弹性体系的反应谱理论，可以推导出实用的振型分解反应谱法，并且在特定的条件下，还可推导出更为简单实用的底部剪力法。