1）反应谱

从式（3-16）、式（3-17）和式（3-18）可以看出，在选定地面运动加速度时程曲线和阻尼比时，最大位移反应Sd、最大速度反应Sv和最大绝对加速度反应Sa仅仅是体系的圆频率ω即自振周期T的函数。如果以体系自振周期T为横坐标，最大绝对加速度反应Sa为纵坐标，可以绘出一条曲线，称为加速度反应谱。因此，所谓的反应谱是指单自由度弹性体系在给定的地震作用下，体系的某个最大反应量（如最大位移反应Sd、最大速度反应Sv、最大绝对加速度反应Sa等）与体系自振周期T的关系曲线。

图3-5（a）、（b）、（c）给出了根据El-Centro地震N-S方向加速度记录所计算出的不同阻尼比的位移、速度和加速度反应谱。图3-6给出了不同场地条件的平均加速度反应谱。

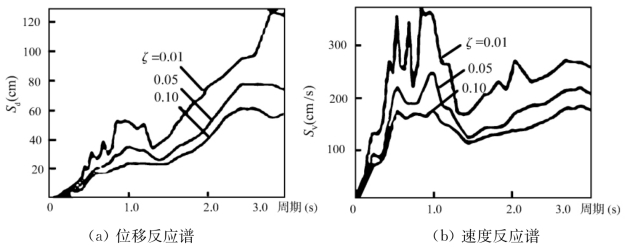
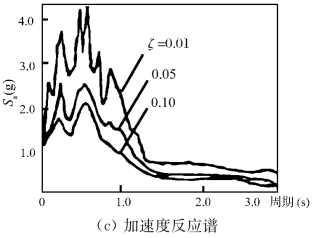
图3-5　El-Centro地震波的反应谱

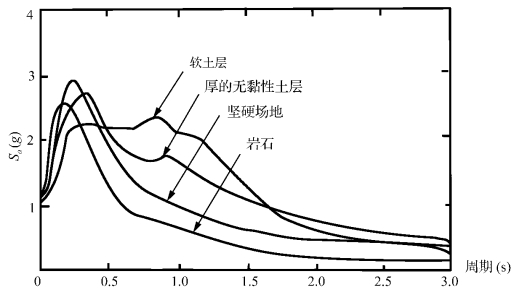
图3-6　不同场地条件的平均加速度反应谱（ζ＝0.05）

从图3-5和图3-6可以看出，结构的阻尼比和场地条件对反应谱的影响很大。此外，分析研究表明，反应谱曲线的形状还取决于建筑场地类别、震级和震中距等因素。

2）设计反应谱

地震是随即的，即使在同一地点、相同的地震烈度，前后两次地震记录到的地面运动加速度时程曲线也有很大差别。在进行工程结构设计时，无法预知该建筑物将会遭遇到怎样的地震，因此无法确定相应的地震反应谱。因此，必须按场地类别、近震和远震分别绘出反应谱曲线，然后根据统计分析从大量的反应谱曲线中找出每种场地和近、远震有代表性的平均反应谱曲线，作为设计用的标准反应谱曲线。这种反应谱称为抗震设计反应谱。

我国《建筑抗震设计规范》（GB 50011—2010）给出的设计反应谱不仅考虑了建筑场地类别的影响，也考虑了震级、震中距和阻尼比的影响，如图3-7所示。

图3-7中的特征周期Tg应根据场地类别和设计地震分组按表3-2采用，当计算8、9度罕遇地震作用时，特征周期应增加0.05s。

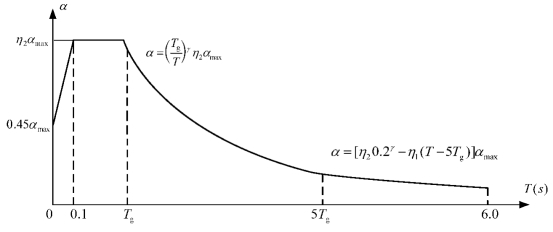
图3-7　地震影响系数曲线

α—地震影响系数；αmax—地震影响系数最大值；η1—直线下降段的斜率调整系数；
γ—衰减指数；Tg—特征周期；η2—阻尼调整系数；T—结构自振周期

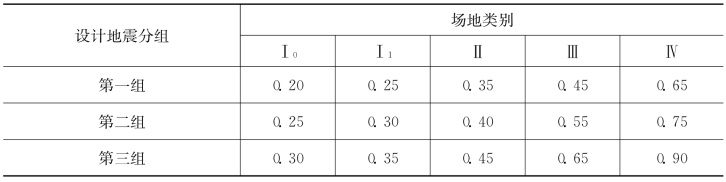
表3-2　特征周期值（s）

（1）水平地震影响系数最大值αmax的确定

由式（3-23）得知，水平地震影响系数α是地震系数k和动力系数β的乘积。地震系数k反映场地基本烈度的大小，基本烈度愈高，地震系数k值愈大，而与结构性能无关。地震系数k与基本烈度的关系如表3-3所示。

表3-3　地震系数k与基本烈度的关系

(www.daowen.com)

当基本烈度确定后，地震系数k为常数，水平地震影响系数α的值仅随动力系数β的值而变化。通过大量的分析计算，我国《建筑抗震设计规范》（GB 50011—2010）将最大动力系数βmax取为2.25。所以水平地震影响系数最大值αmax＝βmaxk＝2.25k，这是与基本烈度对应的水平地震影响系数最大值αmax。

目前，我国建筑抗震采用的是两阶段设计法。第一阶段进行结构强度与弹性变形验算时采用多遇地震烈度，其地震系数k值相当于基本烈度所对应k值的1/3。第二阶段进行结构弹塑性变形验算时采用罕遇地震烈度，其地震系数k值相当于基本烈度所对应k值的1.5～2倍（烈度越高，k值越小）。由表3-3及αmax的计算公式，可得各设计阶段的αmax值，如表3-4所示。

表3-4　水平地震影响系数最大值αmax

（2）阻尼对地震影响系数的影响

建筑结构地震影响系数曲线图3-7的阻尼调整和形状参数应符合下列要求：

①除有专门规定外，建筑结构的阻尼比应取0.05，地震影响系数曲线的阻尼调整系数应按1.0采用，形状参数应符合下列规定：

A.直线上升段，周期小于0.1s的区段。

B.水平段，自0.1s至特征周期区段，应取最大值αmax。

C.曲线下降段，自特征周期至5倍特征周期区段，衰减指数应取0.9。

D.直线下降段，自5倍特征周期至6s区段，下降斜率调整系数应取0.02。

②当建筑结构的阻尼比按有关规定不等于0.05时，地震影响系数曲线的阻尼调整系数和形状参数应符合下列规定：

A.曲线下降段的衰减指数应按下式确定：

B.直线下降段的下降斜率调整系数应按下式确定：

当η1小于0时取0。

C.阻尼调整系数应按下式确定：

当η2小于0.55时，应取0.55。