所谓单质点弹性体系,是指可以将结构参与振动的全部质量集中于一点,用无质量的弹性直杆支承于地面上的体系。例如,水塔、单层房屋等(图3-1),由于它们的质量大部分集中于结构的顶部,所以通常将这些结构都简化成单质点体系。
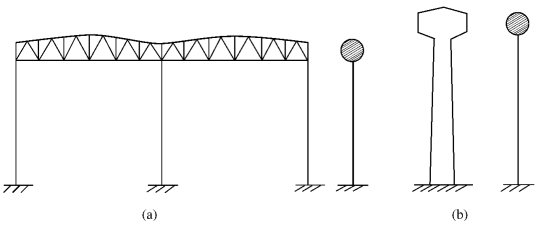
图3-1 单质点弹性体系
地震时地面运动有3个分量,即2个水平分量和1个竖向分量。一个单质点弹性体系在单一水平地震作用下,可以作为一个单自由度弹性体系来分析。为了研究单质点弹性体系的地震反应,应首先建立体系在地震作用下的运动方程。
1)运动方程的建立
图3-2为单自由度弹性体系在地震时地面水平运动分量作用下的运动状态。其中xg(t)表示地面水平位移,是时间t的函数,它的变化规律可由地震时地面运动实测记录求得;x(t)表示质点相对于地面的相对弹性水平位移或相对水平位移反应,它也是时间t的函数,是待求的未知量。
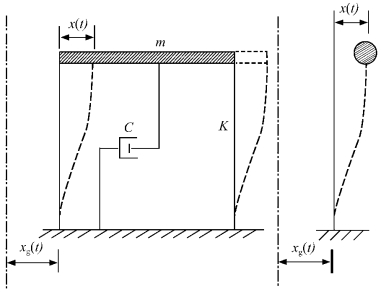
图3-2 单自由度弹性体系在水平地震作用下的变形
为了建立体系在地震作用下的运动方程,取质点m为隔离体,由结构动力学可知,该质点上作用有3种随时间变化的力,即惯性力I(t)、阻尼力R(t)和弹性恢复力S(t)。
惯性力I(t)是质点的质量m与绝对加速度![]() 的乘积,但方向与质点运动加速度方向相反,即
的乘积,但方向与质点运动加速度方向相反,即
![]()
式中:m——质点的质量;
![]() ——质点相对于地面的加速度;
——质点相对于地面的加速度;
![]() ——地面运动加速度。
——地面运动加速度。
阻尼力R(t)是使体系振动不断衰减的力,它来自于外部介质阻力、构件和支座部分连接处的摩擦和材料的非弹性变形,以及通过地基变形的能量耗散等。在工程中一般采用黏滞阻尼理论来确定阻尼力,即假定阻尼力的大小与质点相对于地面的速度成正比,但方向与质点相对速度方向相反,即
![]()
式中:c——阻尼系数;
![]() ——质点相对于地面的速度。
——质点相对于地面的速度。
弹性恢复力S(t)是使质点从振动位置恢复到原来平衡位置的一种力,其大小与质点相对于地面的位移x(t)和体系的抗侧移刚度成正比,方向与质点的位移方向相反,即
![]()
式中:K——体系的抗侧移刚度,即质点产生单位水平位移时在质点处所施加的力。
根据达伦倍尔(D'Alembert)原理,质点在上述3个力作用下处于平衡,则单自由度弹性体系的运动方程可以表示为
I(t)+R(t)+S(t)=0
即
![]()
式(3-4)即为单自由度弹性体系的运动方程,是一个常系数二阶非齐次线性微分方程。为便于方程的求解,将式(3-4)两边同除以m,得
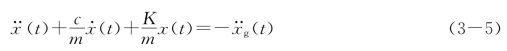
令

则式(3-5)可写成
![]()
式中:ζ——体系的阻尼比,一般结构工程的阻尼比在0.01~0.20之间;
ω——无阻尼单自由度弹性体系的圆频率,即2π秒时间内体系的振动次数。
式(3-7)就是所要建立的单质点弹性体系在地震作用下的运动微分方程。
2)运动方程的解
式(3-7)是一个二阶常系数线性非齐次微分方程,它的解包含两部分:一部分是对应于齐次微分方程的通解;另一部分是微分方程的特解。前者代表体系的自由振动,后者代表体系在地震作用下的强迫振动。
(1)齐次微分方程的通解
对应方程(3-7)的齐次方程为
![]() (https://www.daowen.com)
(https://www.daowen.com)
根据微分方程理论,齐次方程(3-8)的通解为
![]()
式中:ω′——有阻尼单自由度弹性体系的圆频率,它与无阻尼弹性体系的圆频率有以下关系:
![]()
当阻尼比ζ=0.05时,ω′=0.9987ω≈ω
A、B——常数,其值可按问题的初始条件来确定。
考虑初始条件,当t=0时,
![]()
其中x(0)和![]() 分别为初始位移和初始速度,将其代入式(3-9),得
分别为初始位移和初始速度,将其代入式(3-9),得
A=x(0)
再将式(3-9)对时间t求一阶导数,并将t=0和![]() 代入,得
代入,得
![]()
将所得的A、B值代入式(3-9),得到体系自由振动位移方程为
![]()
式(3-11)就是方程(3-8)在给定初始条件时的解答。
无阻尼时(ζ=0),有
![]()
由式(3-12)可以看出,无阻尼单自由度体系的自由振动为简谐周期振动,振动圆频率为ω,振动周期T为
![]()
在结构抗震计算中,常用到结构自振周期T,它是体系振动一次所需要的时间,单位为秒(s)。自振周期T的倒数为体系的自振频率f,即体系在每秒内的振动次数,单位为“1/s”或称为赫兹(Hz)。
![]()
由于质量m和刚度K是结构固有的,因此无阻尼体系自振频率或周期也是体系固有的,称为固有频率或固有周期。对于有阻尼单自由度体系的自振频率,由于结构的阻尼比ζ很小,通常可以近似取ω′=ω,也就是在计算体系的自振周期或频率时,可以不考虑阻尼的影响,从而简化了计算。
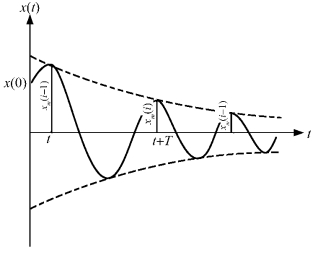
图3-3 有阻尼单自由度弹性体系自由振动的位移时程曲线
由式(3-11)可以看出,有阻尼单自由度弹性体系在自由振动时的位移曲线是一条逐渐衰减的振动曲线,如图3-3所示。其振幅x(t)随时间的增加而减小,阻尼比ζ愈大,振幅的衰减也愈快。将不同的阻尼比ζ代入式(3-11),体系的振动有以下3种情况:
①若ζ<1,则ω′=ω>0,则体系产生振动,称为欠阻尼状态。
②若ζ=1,则ω′=ω=0,则体系不产生振动,此时![]() ,cr=2mω称为临界阻尼系数,ζ称为临界阻尼比。
,cr=2mω称为临界阻尼系数,ζ称为临界阻尼比。
③若ζ>1,则ω′=ω<0,则体系也不产生振动,称为过阻尼状态。
结构的临界阻尼比ζ的值可以通过结构的振动试验确定。
(2)地震作用下运动方程的特解
求运动方程![]() 的特解时,可将图3-4所示的地面运动加速度时程曲线看作是由无穷多个连续作用的微分脉冲组成的。体系在微分脉冲作用下只产生自由振动,只要把这无穷多个脉冲作用后产生的自由振动叠加起来即可求得运动微分方程的解x(t)。
的特解时,可将图3-4所示的地面运动加速度时程曲线看作是由无穷多个连续作用的微分脉冲组成的。体系在微分脉冲作用下只产生自由振动,只要把这无穷多个脉冲作用后产生的自由振动叠加起来即可求得运动微分方程的解x(t)。
![]()
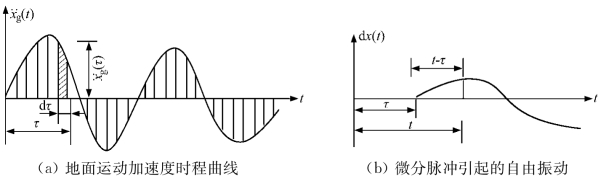
图3-4 有阻尼单自由度弹性体系地震作用下运动方程解答图示
式(3-15)就是非齐次线性微分方程(3-7)的特解,通常称作杜哈梅(Duhamel)积分。它与齐次微分方程(3-8)的通解(3-11)之和就是微分方程(3-7)全解。但是,由于结构阻尼的作用,自由振动很快就会衰减,在地震发生前体系的初始位移x(0)和初始速度![]() 均等于零,公式(3-11)的影响通常忽略不计。
均等于零,公式(3-11)的影响通常忽略不计。
3)地震反应
式(3-15)是单自由度弹性体系在水平地震作用下相对于地面的位移反应。对式(3-15)对时间求导数,可以得到单自由度弹性体系在水平地震作用下相对于地面的速度反应![]() ;单自由度弹性体系在水平地震作用下的绝对加速度为
;单自由度弹性体系在水平地震作用下的绝对加速度为![]() 。经过积分并简化处理,可以得到单自由度弹性体系在地震作用下的最大位移反应Sd、最大速度反应Sv和最大绝对加速度反应Sa,即
。经过积分并简化处理,可以得到单自由度弹性体系在地震作用下的最大位移反应Sd、最大速度反应Sv和最大绝对加速度反应Sa,即
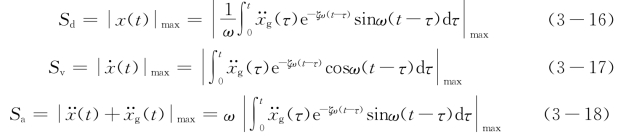
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






