很多时候，构件是按照一定的规律以特定的模数进行变化。所以我们需要把输入值按照需要的规律进行整理转换以后，再作为参数输出。这时就要用到一个比较有趣的函数，它的功能就是我们所熟悉的“四舍五入”。

在Revit中，“四舍五入”的功能被细化为3种不同的方式：“向上取整”“向下取整”“四舍五入”。对应的名称分别是roundup、rounddown、round，如图8-20所示。新建一个族，使用“公制常规模型”族样板，打开“族类型”对话框，添加4个“数值”类型的参数，名称为a、b、c、d，其中d是输入值，之后我们给d赋予不同的值（图8-21、图8-22、图8-23），比较这3个函数处理结果的差异。

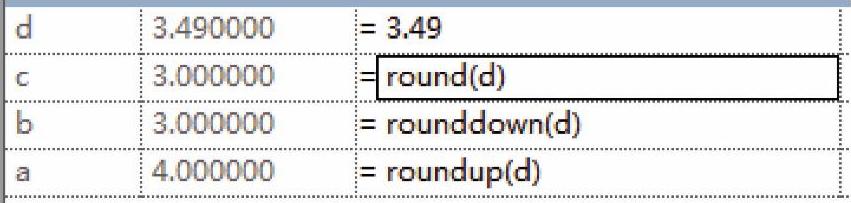
图8-20

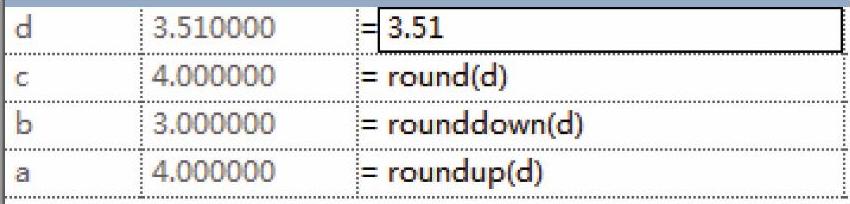
图8-21

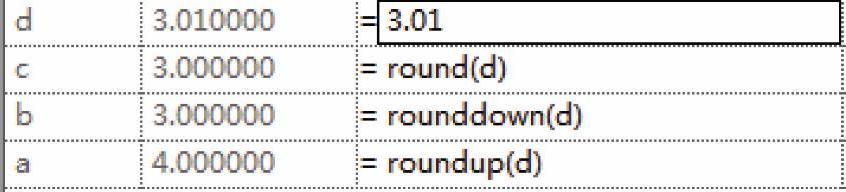
图8-22

图8-23

1）下面我们练习对长度类型的参数进行处理。假设某种情况下，根据所输入的e值，长度f同步地进行变化，规则是当e值每增加到200mm的整数倍时，f的值就增加60mm，如图8-24所示。因为是“增加到200mm”，所以我们选用向下取整来处理输入值，先把输入的参数和“200mm”的这个标准进行比较，再把比较结果处理为整数，最后把这个整数和“60mm”的变化幅度关联起来，赋予参数f。具体格式为“rounddown（e/200mm）∗60mm”，结果如图8-25所示。

图8-24

(www.daowen.com)

图8-25

2）再练习另外一种情况。假设规则是这样的，每千米（公里）计价6元，不足1千米（公里）每300米3元，不足300米的按照300米对待。输入值以“米”为单位。为了操作方便，添加两个“数值”类型的参数，g表示要计算的长度的数值，h表示最后的运费值。

首先我们要处理的是满足单位为千米（公里）时的整数部分，所以在按照1000处理以后，向下取整来得出运费的第一部分，公式为“rounddown（g/1000）∗6”。第二部分是关于“300米”的处理，稍微麻烦一点，我们在前面已经计算过整数公里的基础上，用总长度相减就可以了，即“g-rounddown（g/1000）∗1000”，其中g是总的长度，后半部分是单位为千米（公里）时的整数部分，可以简单理解为“除以千米（公里）取整后再恢复为千米（公里）”，这样就消除了单位为千米（公里）时的小数点后面的数字。这个相减的结果再去和“300米”进行比较，方法和前面的一样（“除以300再取整再乘以单位距离的运费”），写为“roundup（……/300）∗3”，其中省略的部分，就是去掉整数千米（公里）的那部分。完整的公式如图8-26所示。务必多输入几个数字测试一下，看是否满足规则的要求：如图8-27和图8-28所示。

图8-26

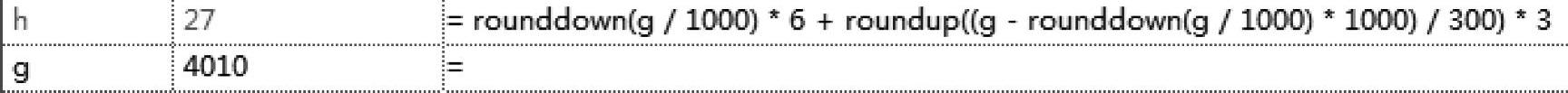
图8-27

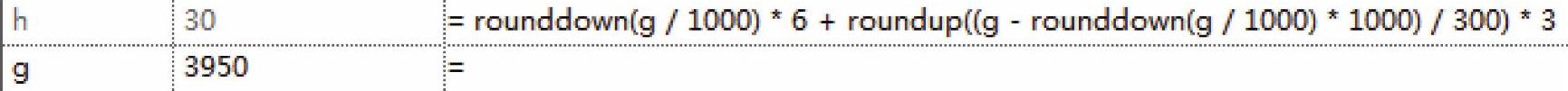
图8-28

这时会发现一个奇怪的现象：距离短反而价格高。这是由规则里的计算方法而导致的，我们检查一下950和1010就可以看出来，950米时计算结果是3∗4=12，1010米时是6+3∗1=9，所以这个不合理的结果是从规则内部产生的，而不是计算公式。

学完本节以后，可进行以下拓展练习：

1）修改最后一个练习的规则，比如，每千米（公里）计价10元，不足1千米（公里）每300米3元，不足300米的按照300米计算”。

2）把长度的变化转换为一个角度参数的变化。