在计算驼峰解体能力时，其影响因素错综复杂，下面就一些主要影响因素进行分析，并说明其确定方法。

1．妨碍时间

在峰前到达场进口或出口咽喉处，由于敌对进路交叉，导致延误驼峰调车机车挂车或推峰分解，一昼夜中断驼峰解体作业的时间称为妨碍驼峰解体时间。

妨碍驼峰解体时间，与编组站站型、峰前到达场的咽喉构造、进站线路的衔接、有无峰下跨线桥以及峰顶配备的调机台数等因素有关。

产生妨碍时间的几种主要情况如下：

（1）客车妨碍。

旅客（通勤）列车横切峰前到达场出口咽喉妨碍驼峰调车机车分解车列[见图4-4（a）]，一昼夜的妨碍时间为

式中 n客——一昼夜各种旅客（通勤）列车横切驼峰前到达场出口咽喉的次数；

t客——各种旅客（通勤）列车每次占用咽喉的时间，包括准备进路、开放信号和列车通过咽喉区的时间，min。

此项时间可作为固定作业时间。若在交接班时通过咽喉区可以不予计算。

（2）反接妨碍。

到达场出口咽喉反驼峰方向接改编列车妨碍驼峰调车机车分解车列。一昼夜的妨碍时间可根据概率论原理确定[见图4-4（b）]。

当到达场反接线群有两排平行渡线时，设 n1为反接列车数，n2为顺接列车数，S1为反接线路数，S 为到达场总线路数，反接妨碍驼峰解体的时间可按下列两种情况分别确定：

① 当时，即每条线平均反接的列车数小于到达场平均每条道的接车数。每条反接线的反接概率为

每条反接线推峰的概率为

8 道反接时不妨碍任何道推峰，其妨碍时间为零；

7 道反接时妨碍8 道推峰，其概率为 P1 P2 ；

6 道反接时妨碍7、8 道推峰，其概率为 P1 （P2+P2）＝2P1 P2；

5 道反接时，妨碍6、7、8 道推峰，其概率为 P1 （P2+P2+P2）＝3P1 P2

依此类推，故到达场反接妨碍推峰解体的概率为

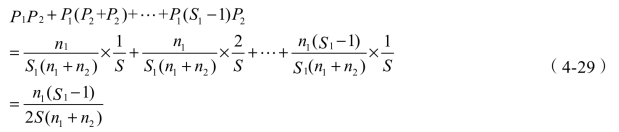
一昼夜推峰解体与反接交叉的次数为

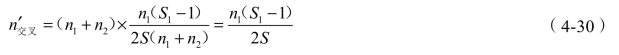
平均每次交叉妨碍驼峰解体时间为

式中 t推——推峰占用交叉点时分；

t分′解——分解车列占用交叉点时分；

t接——反接列车一次占用交叉点的时分。

一昼夜反接列车妨碍驼峰解体的时间为

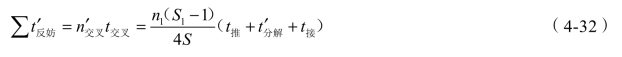
② 当时，即每条反接线反接的列车数大于到达场平均每条线的接车数，则每条反接线推峰的概率为

每条反接线的反接概率与情况①相同。

故一昼夜推峰解体与反接列车的交叉次数为

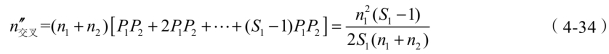
每次交叉平均妨碍驼峰解体时间与情况①相同。故一昼夜反接妨碍驼峰时间为

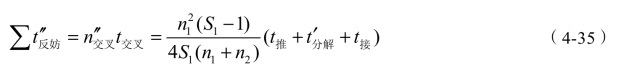
应当指出：上述计算公式仅适合于反接线峰前咽喉构造有双排平行渡线的情况。当咽喉构造发生变化时，其一昼夜的交叉次数的计算公式将有所不同，但仍可参照上述公式应用概率原理进行计算。

（3）挂机妨碍。

改编列车自到达场入口咽喉到达妨碍驼峰调车机车连挂车列而延误驼峰分解车列的时间，仍可应用概率的原理进行确定[见图4-4（c）]。

设该咽喉处接车为优先进路，调车机连挂为次要进路，则只能延误调车机连挂，不能延误接车。若 n1，n2分别为一昼夜到达的改编列车数和每列改编列车调车机连挂次数，t1，t2为接车和连挂一次占用咽喉交叉点的时间。

一昼夜延误调机连挂的概率为

一昼夜延误连挂的次数为

每次延误连挂时间最大为（t1+t2），最小为0，平均为。则一昼夜妨碍驼峰机车挂车的时间为

平均每解体一列车摊到的挂车妨碍时间为

式中 n解——昼夜该台调机解体的列车数。

必须指出：此项连挂妨碍时间应计入t空程当驼峰只配备2 台调机，且t空程较大时，可能对驼峰解体能力产生影响。当驼峰调机配备3 台及以上时，一般调车机连挂即便与接车有交叉妨碍，也来得及推峰，不会影响驼峰解体能力。

（4）机车妨碍。

在到达场出口咽喉处，本务机车入段妨碍驼峰调机推峰解体[见图4-4（d）]。此项妨碍时间只有在无峰下跨线桥，并在到达场入口处无第二条入段通路时才产生。在计终时只应考虑到达场上侧那部分线路的本务机车入段，而下侧那部分线路的本务机可利用驼峰调车机推峰离开交叉点后的空档入段，不会妨碍驼峰机车推峰。故其妨碍时间可按式4-40 计算

式中 n机，t机——每昼夜入段机车台数和每次入段占用咽喉时间；

β——采取部分本务机利用驼峰调机下峰整场时横越驼峰前出口咽喉或经由入口咽喉绕行入段等措施以后，一昼夜横跨驼峰的本务机车占总入段机车的比重。

平均每解体一列车摊到的机车妨碍时间为

（5）妨碍驼峰解体时间计算举例。

已知：某编组站到达场详图如图4-4所示，配备两台调车机实行双推单溜，甲调负责1～3 道列车解体，乙调负责5～8 道列车解体。一昼夜共计到达改编列车80 列，其中1～3 道顺接36 列，5～8 道顺接22 列，反接22 列，t推=5 min，t推′=8 min，t 接＝7 min，t机=2 min，n客=2列，t客=6 min，试计算该驼峰的妨碍时间。

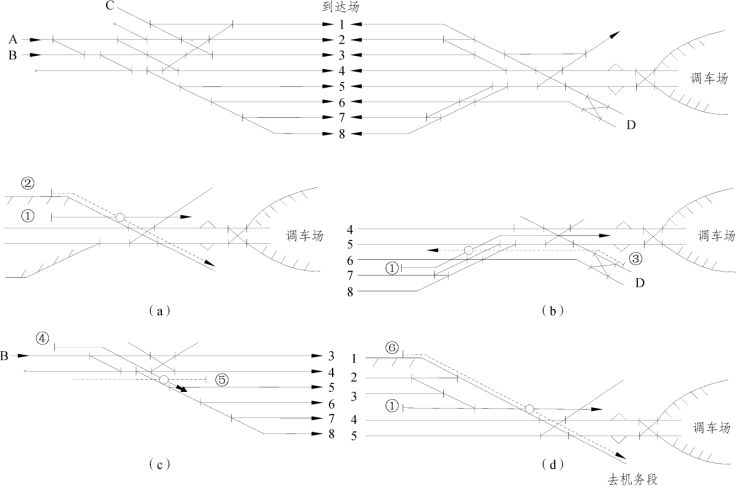
图4-4　妨碍驼峰解体时间计算举例

① 推峰解体；② 客车通过；③ 列车反接；④ 列车到达；⑤ 调机折返；⑥ 机车入段

① 计算 ∑t客妨：

② 计算 ∑t反妨：

由于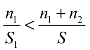，即

故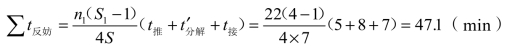

③ 计算 ∑t挂妨：

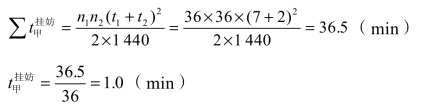
乙调可通过采取措施，不妨碍驼峰机车解体，故可不必计算挂车妨碍时间。

④ 计算 ∑t机妨：

由于1、2、3、4 道部分本务机车必须横切驼峰推送线入段，n机＝36，t机＝36，β＝50%，则∑t机妨＝36×2×0.5＝36，min。

上述t挂妨计入空程中，∑t客妨计人固定作业时间中，则实际一昼夜摊到每解体一列车的妨碍时间为

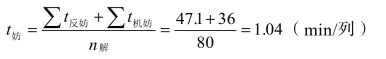
2．整场时间(www.daowen.com)

驼峰调车机车下峰整理车辆产生的中断驼峰作业时间称为整场时间，它包括：

（1）为腾出空线使车组能自驼峰继续溜放，驼峰机车下峰将线路上的车辆连挂（“推场子”），而产生的驼峰作业中断时间。

（2）为恢复调车场线路固定使用，驼峰机车下峰将混线的车辆进行整理，而产生的驼峰作业中断时间。

影响整场时间的主要因素有：

（1）调车场采用的调速方式：调车场调速系统可大大提高车辆的连挂率，减少“天窗”，据不完全统计，在调车场内安装减速器或减速顶以后，车辆连挂率可达到97%，每列车平均的整场时间可减少33%～48%。

（2）调车场线路的有效长度及线路数量：调车场线路的有效长度应满足列车长度加20%的要求，以保证必需的“天窗”和安全距离。显然，调车场线路有效长能满足上述要求时，则下峰“推场子”的时间和次数可以减少。调车场的线路数量规定应保证每一个组号设一条，当该到达站每昼夜的车流大于200 车时，应增设一条，如线路数量满足不了这个要求，就会产生“借线”或“共用”等情况，使整场时间增加。

（3）解体钩数：驼峰每昼夜解体的钩数对整场时间有一定的影响。大组车多，“天窗”数就少；碎钩车多，“天窗”就多，则下峰次数也会增加。

（4）气候条件：下雨、雾天视线不好，影响瞭望，使制动准确性降低，车辆连挂率降低。顺风溜放，有利于车辆连挂，而逆风又会使“天窗”加大。另外，气候严寒，车辆容易凝轴，制动距离不易掌握，都直接影响整场时间。

（5）此外，调车和制动人员的技术水平，驼峰头、尾部作业分工等都对整场时间有影响。

整场时间可以采用写实査定的方法求得，每解体一列车的平均整场时间

式中 ∑t整场——每昼夜该驼峰调车系统查定的总整场时间，min；

n解——查定期间该驼峰解体的列车数。

3．解送禁溜车时间

解送禁溜车可按解禁溜车与送禁溜车两个过程分别进行查定。解禁溜车是指在解体过程中将车列中禁止溜放的车辆送往禁溜线的作业，其时间应自调车机停止溜放车组时起至将禁溜车送往禁溜线或迂回线后返回驼峰峰顶时止。送禁溜车是指驼峰调车机将存放在禁溜线或迂回线上的禁溜车送往峰下固定线路的作业，或者是解体过程中将挂在车列中的禁溜车直接送往峰下线路的作业。

影响解送禁溜车时间的因素有下列几项：

（1）车列中禁溜车的数量：禁溜车钩数多，解送禁溜车的时间会增加。

（2）禁溜车组在车列中的位置：禁溜车挂在解体车列的首部，解送时间要长；相反，禁溜车挂在解体车列尾部，由于在调机的机后，解送时间可大大缩短。

（3）峰顶禁溜线的出岔位置：当禁溜线的辙叉设在峰顶平台上时，送禁溜车需后退，所需时间增加；当禁溜线的道岔尖轨设在平台上时，送禁溜车不必后退，可节省送禁溜车的时间。

每解体一车列平均摊到的解送禁溜车时间可用写实查定方法按式（4-43）进行计算。

式中 ——每昼夜查定的解、送禁溜车时间；

n解——查定期解体的列车数。

4．驼峰间隔时间

驼峰间隔时间是指第一车列在峰顶溜放完毕调车机停轮时起至第二车列开始溜放时止的最小技术间隔时间，它包括转换道岔、开放驼峰信号、司机确认信号和车列自预推停车点起动至将车列的第一辆车推至驼峰信号机处等项作业时间。

驼峰间隔时间与驼峰作业组织方式、驼峰上采用的调机台数、推送线上预推停车点离驼峰信号机的距离、预推速度等项因素有关。

（1）单推单溜的最小间隔时间。

驼峰只配备1 台调车机车，其间隔为

式中 t空程——调车机车空程走行时分；

t推——驼峰机车挂车后将车列第一辆车推送至驼峰信号机处的时间。

（2）双推单溜的最小间隔时间。

驼峰上配备两台及其以上机车，其间隔为

式中 t岔——转换道岔、开放驼峰信号时间，min；

t确——司机确认信号时间，min；

l续推——续推距离，m；

v续推——续推速度，km/h。

当驼峰只配备两台调机，且（t空程+t推）>（t分解+t禁溜+）时，其间隔时间需附加空程时间Δt

式中 t推＝t预推+t续推。

（3）双推双溜的最小间隔时间。

这时驼峰配备3 台及其以上调车机，其间隔时间应分别一峰、二峰按式（4-47）计算：

式中 v空′——驼峰机车从峰顶返回至预推停车点的平均速度，km/h。

其他符号意义同前。

5．辅助生产时间

（1）交接班时间。

式中 n交接——每昼夜交接班次数，三班制时为2 次，四班制时为3 次；

t交接——平均每次交接班时间，可取20～25 min，实行四班制时，应增加夜间一次交接班时间10～15 min，减少一次吃饭时间。

（2）吃饭时间。

式中 n吃饭——每昼夜吃饭次数，可取2 次；

t吃饭——平均每次吃饭时间，可取30 min。

（3）整备时间。

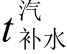式中 ，——蒸汽机车加煤上水（50 min）和至整备地点的走行时间，min；，——蒸汽机车补水和（25～30 min）至补水地点的走行时间，min。

式中 ，——内燃机车整备（30 min）和至整备地点的走行时间，min。

内燃调车机车每2～4 天还应增加一次加油时间，每次不得超过50 min（具体时间由车站、机务，根据机车油箱大小及耗油量等条件共同查定）。

6．推送速度

驼峰的推送速度是确定驼峰解体能力的关键，也是衡量驼峰效率的重要指标。若驼峰配备两台调车机，实行双推单溜，采用直接计算法有关公式，可计算出在不同推送速度v解和不同列车编成m 时，驼峰的解体能力如表4-1所示。由表4-1可知：

表4-1　两台调机双推单溜解体能力表

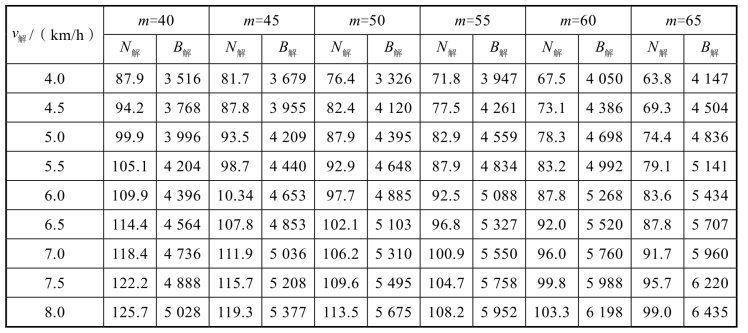
注：①t空程＝6.78，t预推＝4.0，t禁溜＝1.0，t妨碍＝0.5，t间隔＝3.0；
②t解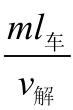＝，l车＝14.3 m；
③∑t交接＝50，∑t吃饭＝60，∑t整备＝40，∑t客妨＝0，∑t取′送＝0。

（1）驼峰解体能力随v解的增加而上升，其递增值不是呈线性上升，而是随v解的增加而逐渐减弱。提高v解至一定值（如6 km/h）有利于增加驼峰的解体能力。

（2）当v解为定值时，以列数计的解体能力将随列车编成辆数m 的增加而降低；以辆数计的解体能力将随m 的增加而增加。因此，驼峰解体能力应以改编车数为主，辅以改编列数同时进行衡量。

（3）当v解为定值时，以列数计的解体能力将随列车质量的提高而递减约4.8%，但以辆数计的解体能力将随列车质量的提高而递增4.7%。因此，提高列车质量，开行可过峰的重载列车，将对驼峰能力产生正面效应，即可用较少的调车程，完成较多的改编辆数。

7．驼峰调车机车台数和作业组织方式

驼峰的解体能力与峰上配备的调车机台数以及驼峰采用的作业组织方式有关。现按到达场与调车场纵列的编组站三种不同作业方案，分别求算其解体能力（见表4-2）。

表4-2　不同调机台数和作业组织方式的解体能力

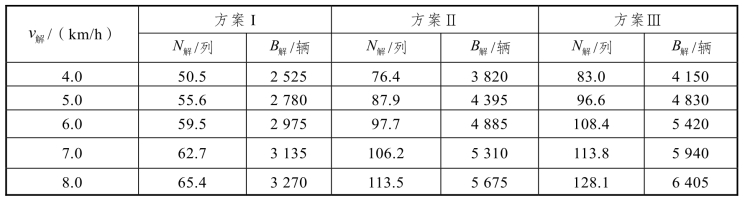
方案Ⅰ：一台调车机实行单推单溜；

方案Ⅱ：两台调车机实行双推单溜；

方案Ⅲ：两台半调车机实行双推单溜。

第Ⅱ方案与第Ⅰ方案比较，驼峰解体能力提高了64.2%（当v解=6.0 km/h 时）。第Ⅲ方案与第Ⅱ方案比较，其解体能力只提高10.9%（当v解=6.0 km/h 时），能力增加有限。因此，用于驼峰纯解体作业的机车大于两台以上，且交接班，吃饭期间驼峰全部停止作业时，第三台机车充其量只能顶替其他两台机车的整备作业时间，用于纯解体时间不足6.4%，解体能力只增加6～10 列。故一般驼峰用于纯解体的机车台数以配备2～2.5 台为宜。当驼峰需要协助峰尾进行编组作业或下峰整场和取送作业较多时，调机台数可根据峰上峰尾作业分工情况另行确定。