在单线区段，通常采用成对非追踪运行图（见图2-2）。单线成对非追踪平行运行图周期可用下式表示

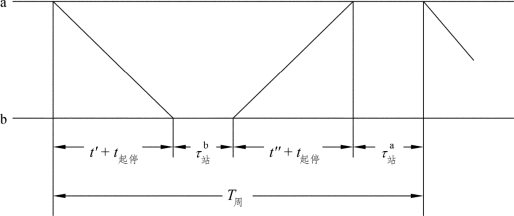
图2-2　单线成对非追踪运行图周期示意图

式中 t′，t′——上下行列车的区间纯运行时分，min；

τ站a，τ站b——a，b 站的车站间隔时间，min；

∑t起停——列车起停附加时分，min。

由于一个周期内所包含的列车数为一对（即n周＝1），因此只要将n周＝1代入式（2-2）～（2-4），即可得相应区间通过能力。

为了使区段通过能力达到最大，应当使限制区间的T周数值尽量缩小。在采用一定类型的机车和一定的列车质量标准的条件下，区间运行时分 ∑t运是固定不变的。因而想要缩小T周，只有设法缩小 ∑t起停+∑τ站的数值。通过在限制区间合理地安排列车运行线的铺画方案，是可以达到上述目的的。如图2-3所示，运行图上列车运行线的可能铺画方案有四种。

（1）上下行列车不停车通过车站而进入区间，见图2-3（a），运行图周期为

（2）上下行列车不停车通过车站而开出区间，见图2-3（b），运行图周期为

（3）下行列车不停车通过区间两端车站，见图2-3（c），运行图周期为

（4）上行列车不停车通过区间两端车站，见图2-3（d），运行图周期为

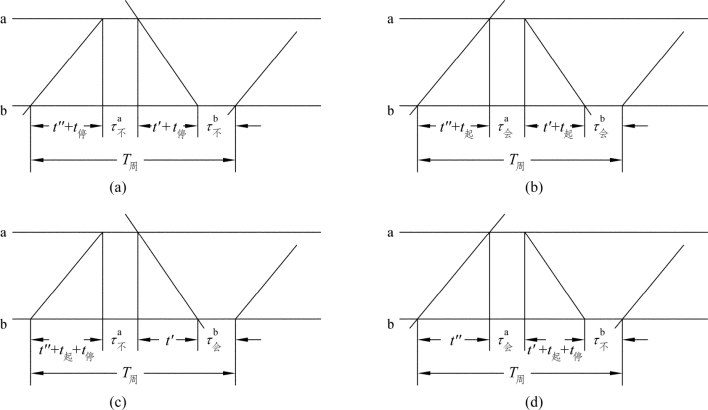
图2-3　列车运行线铺画方案示意图

在选择限制区间列车运行线的合理铺画方案时，应考虑到区间两端车站的具体条件。例如，在a 站下行出站方向有较大上坡道时，如果采用下行列车在a 站停车进入区间的方案，就有可能造成下行列车出发启动困难，这时就应选用下行列车通过a 站而T周又是较小的方案。

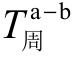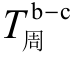中间站的技术作业停留时间，对两相邻区间的通过能力会产生不良影响，并可能因而使相邻区间中的一个成为区段的限制区间，因此必须研究采取消除或减少这种影响的措施。由图2-4可见，当技术作业停车站的邻接区间可能成为限制区间时，应使和尽量缩小，并尽可能使，即

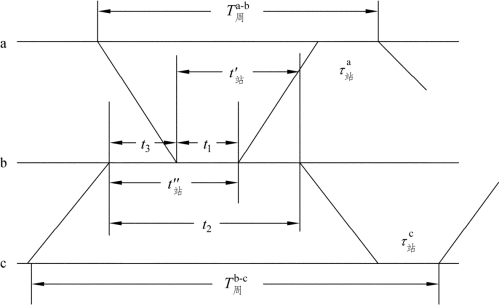
图2-4　列车会车与技术作业停站时间关系示意图

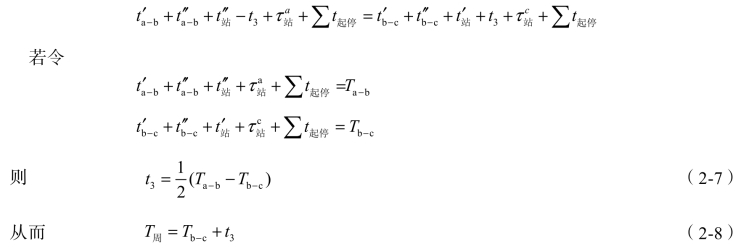
当 Ta-b>Tb-c时，t3 为正值，即应先从b—c 区间接入列车。反之，当 Ta-b<Tb-c时，t3为负值，则应先从a—b 区间接入列车。但此时必须保证 t1≥τ会b，即必须保证t3≤t站′ -τ会b（t站′为先接入列车的技术作业停站时间），如果b 站不允许同时接车，还必须保证t3≥τ不b，此时，T周≥Tb-c+τ不b，否则需要进行调整。

为了减少技术需要停站时间对通过能力的影响，可以根据具体情况采取如下措施：(www.daowen.com)

（1）将技术需要的停车站设在两个列车运行时分较小区间所邻接的车站上。

（2）两列车在技术需要停车站交会时，先从T 较小的区间接入待会列车（例如 Tb-c<Ta-b，则应先从b—c 区间接入列车）。

（3）规定最小的列车技术需要停站时间。

（4）将技术需要停车站设在允许同时接车的车站上。

（5）当技术需要停车站不允许同时接车而邻接区间的列车运行时分又大致相等时，可采取交错会车方式（见图2-5）。如 Ta-b>Tb-c，参照图2-4可知：

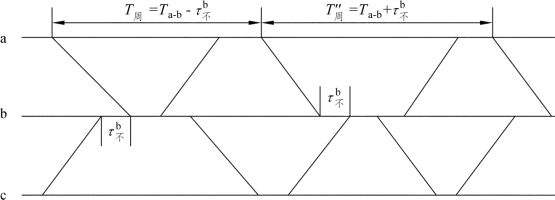
图2-5　交错会车示意图

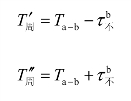
于是

因而，采取交错会车方式的有利条件应是

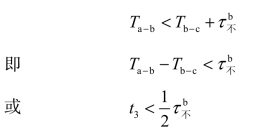
（6）将上下行列车的技术需要停站分别规定在两个车站上，见图2-6。

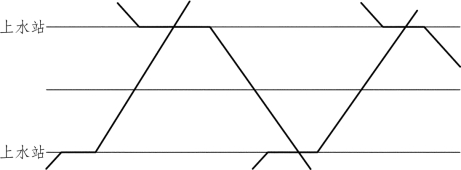
图2-6　上下行列车在两个车站交错上水图

如果无法采用上述措施或虽采用某项措施仍不能消除技术需要停站时间对通过能力的影响时，可采用移动运行图周期的办法（见图2-7）。当一个列车的技术需要停站时间相当于半个运行图周期时，可采用半周期移位法。当一个列车的技术需要停站时间相当于一个运行图周期时，则可采用全周期移位法。采用运行图周期移位法，可以提高通过能力，但旅行速度将显著降低，且要求车站具有较多配线，故一般只在特殊情况下采用。

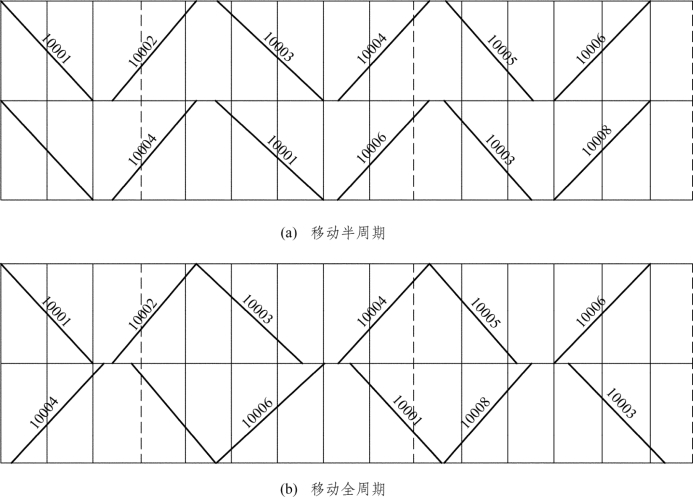
图2-7　移动运行图周期

例如，A—B 区段为单线半自动闭塞区段，有关资料见图2-8。选择合理会车方案时，一般先从困难区间a—b，或从邻接技术作业停车站的区间b—c，c—d 开始，依次进行选择，即可得第一方案。分别计算该方案每一区间的T周，可以看出a—b 区间的T周最大。

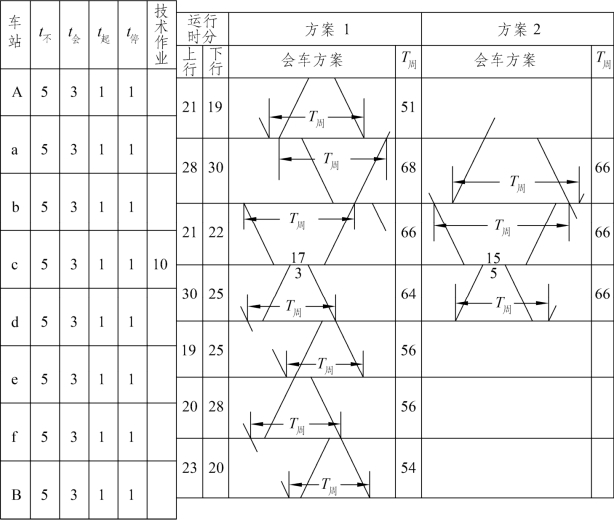
图2-8　列车交会方案

对方案1 中a—b 区间的会车方式加以分析可以看出，它并不是最优的铺画方案，而以上下行列车不停车通过车站开出区间的方式为最优方案。但是，当在a—b 区间采用最优铺画方案时，将使 b—c 区间的运行图周期加大，而成为T周最大的区问。为此，可利用的关系，调整b—f 和f—d 区间的铺画方案，使这时t3≥τ不c，t1≥τ会c，所以不用调整而得方案2。在方案2 中，a—b，b—c 及c—d 三个区间的T周都相等，同时再也找不出使T周进一步缩小的其他会车方式，这样，方案2 便成为通过能力最大的方案，a—b，b—c 及c—d 区间为全区段的限制区间。这时，不考虑T周和d有效的区间通过能力为

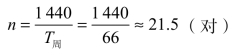
通过能力应保留小数点后一位，平行运行图通过能力不进位为0.5 或1.0，非平行运行图通过能力以对数表示时，不足0.5 者舍去，0.5 以上但不足1 对者按0.5 对计算，以列数表示时，不足1 列者舍去。