若在水平路面上制动，并忽略制动过程中的空气阻力的影响，则制动过程中作用于汽车前后轴的地面垂直反力F_z1、F_z2的值可以用式（5-3）计算。

令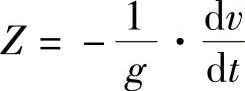，称为制动强度，则式（5-3）可以写为

若在附着系数为ϕ的路面上制动，前、后车轮都达到抱死（不论是同时抱死或分别先后抱死）时，汽车的地面制动力等于附着力，即F_b=ϕ_G，制动强度为Z=ϕ。因此，作用于前后车轮的地面法向反作用力为

式（5-12）说明，当附着系数和制动强度变化时，作用于前后轴的法向反作用力发生相应变化。作用于前轴的载荷增大，而作用于后轴的载荷减小。此轴荷变化将对汽车的制动过程产生重要影响。

随着制动强度增长，其前后轴附着率也增长，直至等于峰值附着系数ϕ_p或滑动附着系数ϕ_s（车轮抱死拖滑）。因此，要保证汽车在制动过程的稳定性，前轮的附着率φ₁必须始终大于后轮的附着率φ₂，因为这样才能使前轮的附着率φ₁先达到滑动附着系数ϕ_s，使前轮先于后轮抱死拖滑。即应满足：

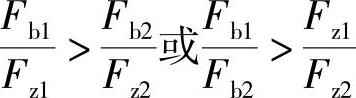
在车轮抱死拖滑前，当φ₁、φ₂的值均小于峰值附着系数ϕ_p或滑动附着系数ϕ_s时，制动器制动力F_μ等于地面制动力F_b，即F_μ1=F_b1、F_μ2=F_b2。因此，制动稳定性条件可写为

制动稳定性的极限条件为

(www.daowen.com)

显然有

F_μ1+F_μ2=ZG （5-15）

当汽车前后轮同时抱死拖滑时，有

Z=ϕ （5-16）

式（5-14）和式（5-15）表达了保证制动稳定性的两个条件，消去变量Z，可得

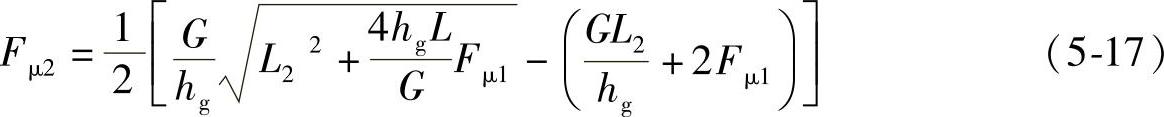
式（5-17）为满足制动稳定性极限条件的F_μ1和F_μ2的关系式，即：使前后车轮同时抱死拖滑时，其前后制动器制动力F_μ1和F_μ2的所应满足的关系。该关系式决定了一条曲线，常称为理想的前、后轮制动器制动力分配曲线，简称Ⅰ曲线。

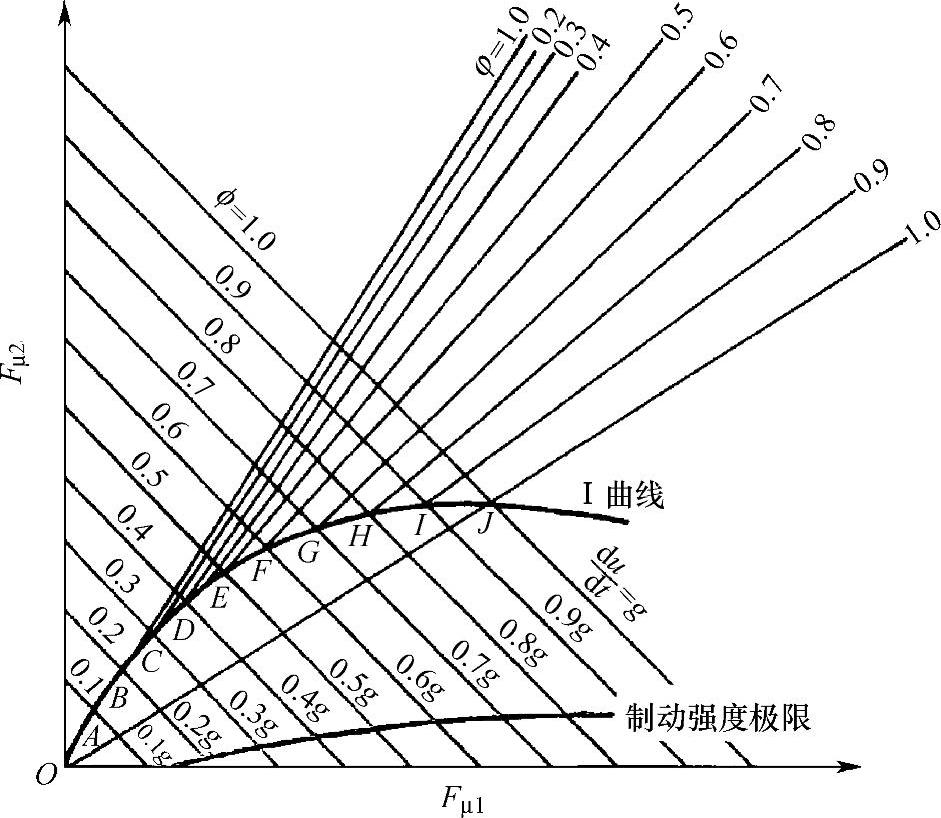
图5-19 理想的前后制动器制动力分配曲线

用作图法可直接得到Ⅰ曲线。首先，取不同ϕ值（ϕ=0.1，0.2，0.3，…），根据式（5-15）和式（5-16），得到一组平行线，如图5-19所示；然后，再把不同ϕ值（ϕ=0.1，0.2，0.3，…）代入式（5-14）和式（5-16），也绘于图5-19上，得到一组通过坐标原点、斜率不同的射线。这两组直线中，对于某一ϕ值，均可找到两条直线，这两条直线的交点在横、纵坐标轴上的对应值，便是满足制动稳定性极限条件的F_μ1和F_μ2的值。对应于若干个ϕ值，以同样方法可相应得到若干个点。把这些点连接起来所形成的曲线即为Ⅰ曲线，该曲线上任意点所决定的F_μ1值和F_μ2值，即为在相应附着系数的道路上前后车轮同时抱死拖滑时，其前后轮制动器所应具有的制动器制动力。

由此可见，只要确定了汽车的总质量m或汽车的总重G、汽车的质心位置（L₁、L₂、h_g），便可作出Ⅰ曲线。