1.滚动阻力的产生
车轮滚动时,轮胎与路面的接触区域产生法向、切向的相互作用力,两者产生相应变形。其相对刚度决定了轮胎和支撑面变形的特点和相对大小。在硬路面(混凝土路、沥青路)上滚动时(动力性分析时的道路条件),弹性轮胎的变形是主要的;在软路面(土路、砂路)上滚动时,路面的沉陷变形是主要的。这些变形伴随着能量损失,是滚动阻力产生的根本原因。
用弹簧轮模型可说明由弹性轮胎变形导致阻力产生的机理,如图3-6所示。弹簧轮周围分布着一个个小弹簧和减振器,车轮滚动时各个弹簧反复交替经历压缩过程和伸展过程,克服减振器阻尼的作用而消耗阻尼功,表现为车轮的滚动阻力。
滚动阻力产生的原因还可从弹性轮胎受力变形的角度分析。图3-7所示为某轮胎在硬支撑路面上受径向载荷W时的径向变形h曲线。图中:C为加载变形过程曲线,D为卸载变形恢复过程曲线。加载变形过程,外力对弹性轮胎做功,使其变形,C曲线下面积OCABO为该过程中对轮胎做的功;在卸载变形恢复过程中,弹性轮胎变形而具有的弹性势能向外释放做功,使变形恢复,D曲线下面积ADEBA为轮胎恢复变形时释放的功。由于阻尼的存在,两曲线并不重合,其间的面积为加载与卸载过程中的能量损失。此能量消耗在轮胎各组成部分的摩擦以及橡胶、帘线等物质的分子间的摩擦,转化为热能消失在大气中,称为弹性轮胎的迟滞损失。
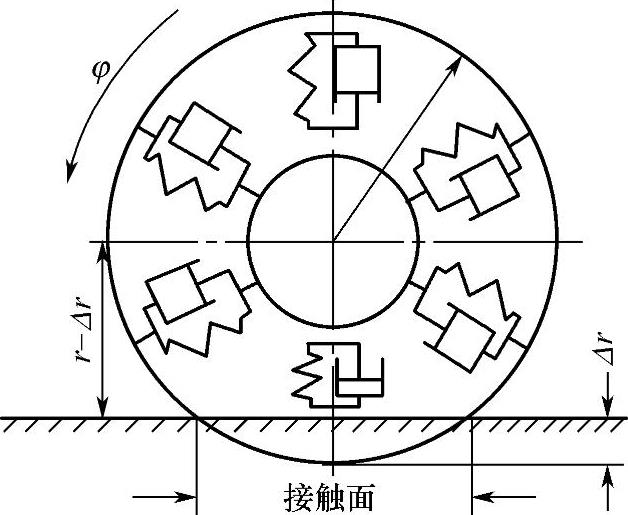
图3-6 弹簧轮模型
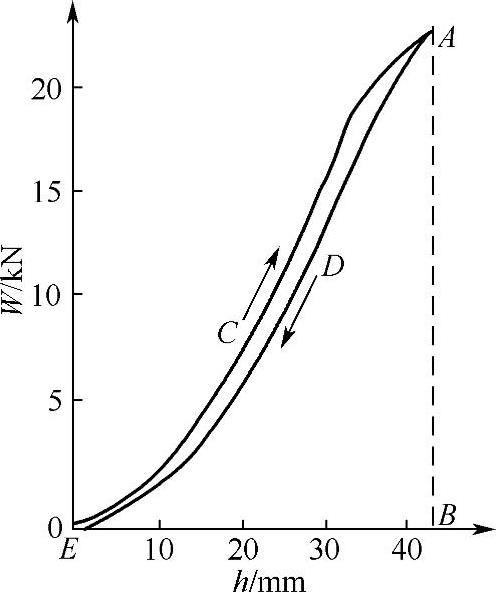
图3-7 某轮胎的径向变形曲线
加载与卸载变形曲线的差异,导致了轮胎接地面上压力分布的变化,产生阻碍车轮滚动的阻力偶和阻力。车轮不滚动时,地面对车轮的法向反作用力的分布前后对称。显然,在法线nn′两侧,同样的变形对应有相同的法向应力;当车轮滚动时,在法线nn′前后两侧相对应点,由于处于压缩变形和恢复变形的不同过程中,相同的变形所对应的法向应力却不同。由于弹性迟滞现象,前部的地面法向反作用力大于后部的地面法向反作用力,使轮胎前后地面法向反作用力的分布不对称,从而使法向反作用力的合力Fz相对于法线nn′向前移动了距离a。若把合力Fz平移至法线nn′,则需添加一阻力偶Tf=Fza,如图3-8所示。
由于弹性车轮滚动时产生了阻力偶,因此若使从动车轮在硬路面上等速滚动,必须相应在车轮中心施加推力Fp1(下标1指前轮),使之与相应的地面切向反作用力构成力偶矩克服Tf。即
Fp1r=Tf
因此
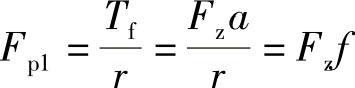
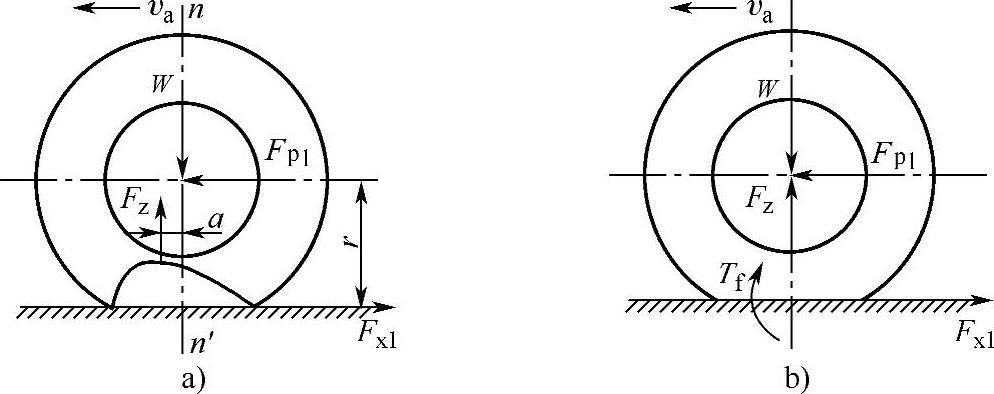
图3-8 弹性轮胎在硬路面上滚动时的受力情况
a)Fz前移 b)产生滚动阻力偶矩
力都是成对出现的,Fx1为推动车轮滚动前进的推力Fp1引起的地面切向反作用力,在此表现为阻碍车轮滚动的滚动阻力Ff。即
Ff=Fx1=Fp1=Fzf (3-6)
f称为滚动阻力系数。显然: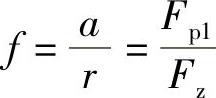 。可见滚动阻力系数指车轮在一定条件下滚动时所需的推力与车轮负荷之比,即单位汽车重力所需的推力。
。可见滚动阻力系数指车轮在一定条件下滚动时所需的推力与车轮负荷之比,即单位汽车重力所需的推力。
这样,在分析汽车行驶阻力时,不必具体考虑车轮滚动时所受到的滚动阻力偶矩,而只要知道滚动阻力系数即可求出滚动阻力。
图3-9为驱动轮在硬路面等速滚动时的受力图。图中:Fx2为驱动力矩Tt所引起的道路对车轮的切向反作用力Fx2(下标2指后轮),Fp2为驱动轴作用于车轮的水平力。由于弹性迟滞现象,驱动轮的法向反作用力的作用点也前移了距离a,因而也产生了滚动阻力偶矩Tf。由平衡条件得
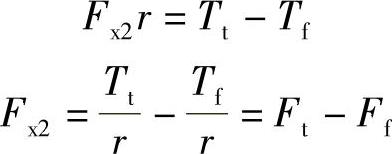
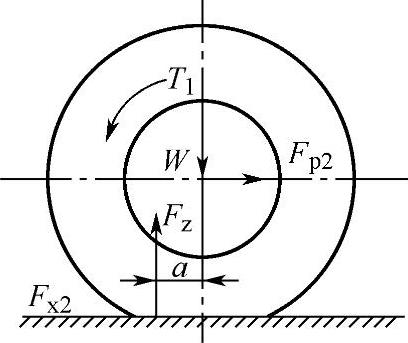
图3-9 驱动轮在硬路面等速滚动时的受力图
由此可见,由于弹性迟滞现象产生的滚动阻力偶矩Tf,也使驱动轮受到滚动阻力Ff的作用。驱动力矩Tt产生的驱动力Ft在克服了Ff后,才能转化为作用在驱动车轮上驱动汽车前进的地面切向反作用力Fx2。
2.滚动阻力系数
滚动阻力Ff的大小取决于滚动阻力系数f,研究汽车的滚动阻力的实质就是研究滚动阻力系数。试验表明:f的大小与路面种类及其状况、行驶车速以及轮胎的构造、材料、气压等有关。
轮胎在不同路面上滚动时的变形量及由此所引起的弹性迟滞损失不同,因而其滚动阻力系数不同。汽车中低速行驶时,其滚动阻力系数的数值范围见表3-3。
表3-3 滚动阻力系数的数值
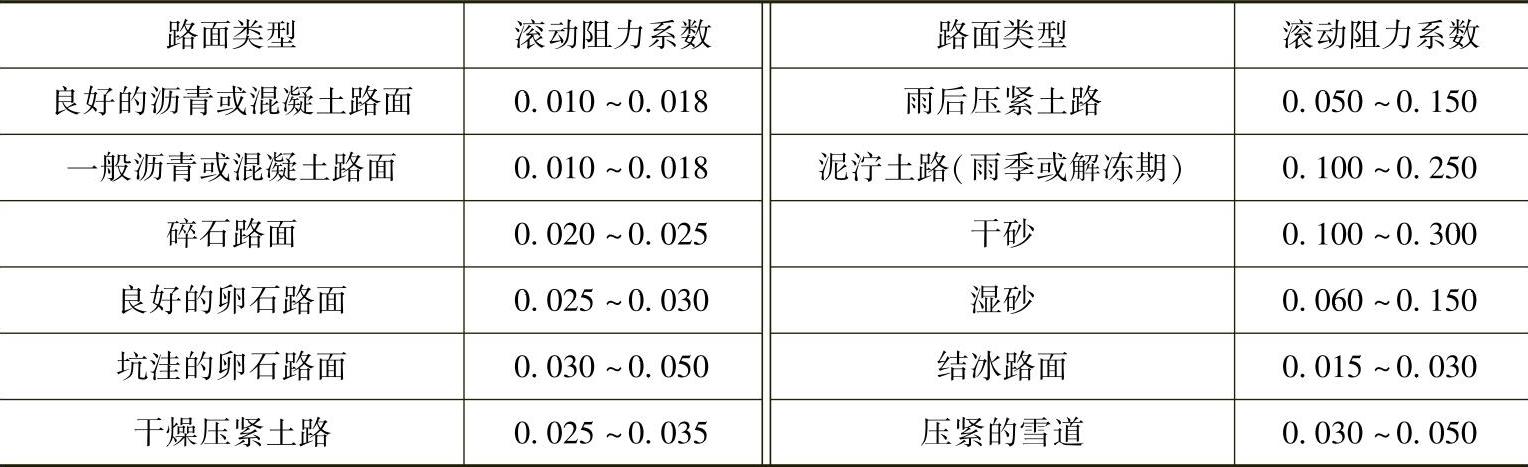
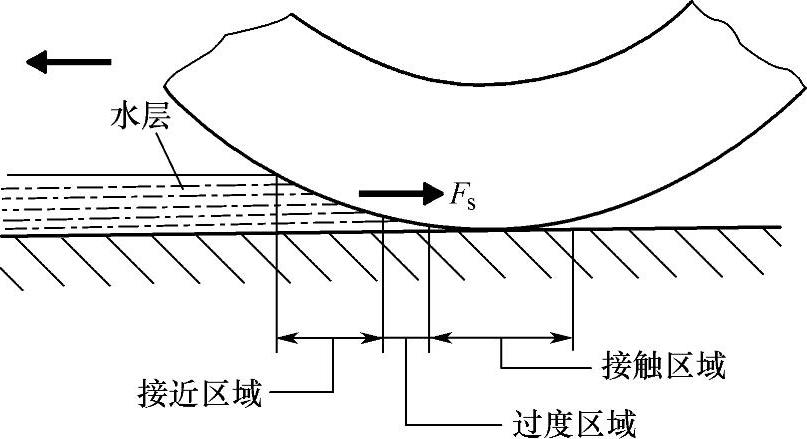
图3-10 车轮在积水硬路面上的滚动
路面状况也影响滚动阻力系数,汽车在坚硬、平整、干燥的路面上行驶时,其滚动阻力要比在破损了的旧路面上小得多;汽车在湿路面上行驶时,车轮必须排挤水层(图3-10),因此滚动阻力通常较在干路面上行驶大得多。(https://www.daowen.com)
行驶车速对滚动阻力系数有很大影响,如图3-11所示。车速低于100km/h时,货车及轿车轮胎的滚动阻力系数随车速逐渐增大,但变化不大。车速高于140km/h时,轿车轮胎的滚动阻力系数值增长较快,且当车速达到某一临界车速时,因轮胎发生图3-12所示的驻波现象,滚动阻力系数迅速增大。
临界车速vl的近似值可用下式估算:
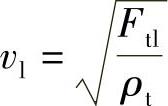
式中 Ftl——轮胎的圆周张力;
ρt——单位面积胎面材料的密度。
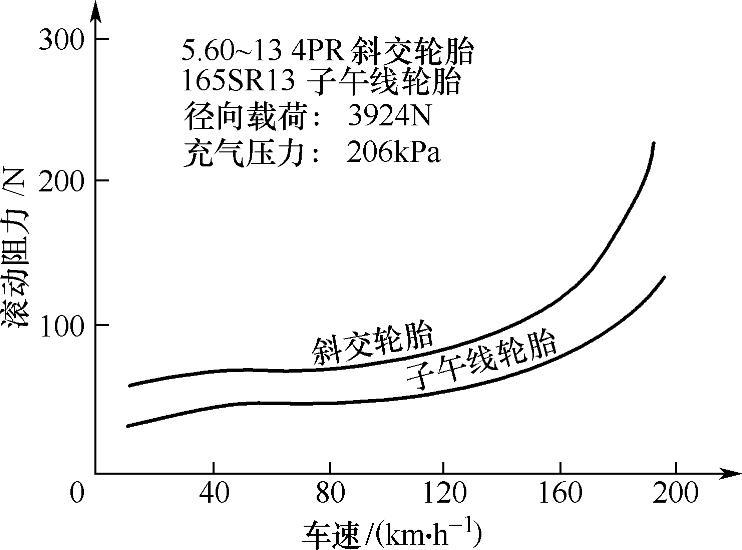
图3-11 车速和轮胎类型对滚动阻力系数的影响
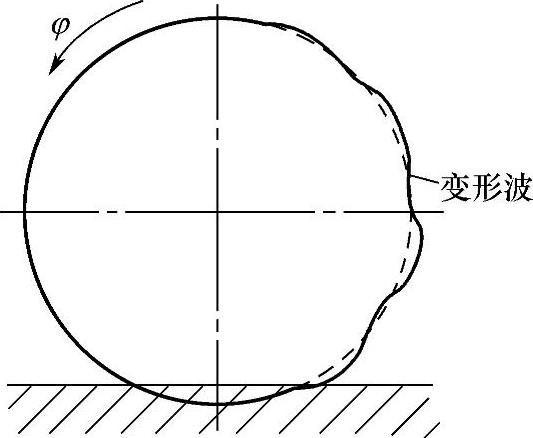
图3-12 胎面圆周上的驻波
汽车以接近临界车速vl的车速行驶时,轮胎离开地面后,胎面因轮胎变形所产生的扭曲不能立即恢复,其残余变形产生了一种波即驻波。此时,轮胎周缘不再是圆形而呈明显的波浪状。轮胎刚刚离开地面时,驻波振幅最大,而后依指数规律沿轮胎圆周衰减。驻波的形成使能量损失显著增大,从而引起大量发热,使轮胎温度很快升高到100℃以上,胎面与轮胎帘布层脱落,极易出现爆胎现象。驻波限定了轮胎安全行驶速度。避免驻波的方法是确定车速的上限值,增大轮胎气压可使产生驻波的临界车速增大,并减小相应的滚动阻力。
轮胎的结构、帘线和橡胶品种不同,轮胎承载后滚动变形量也不同,而且变形后胎面、轮胎内部材料之间的摩擦有很大差异,因此对滚动阻力系数f的值都有影响。
与普通斜交轮胎相比,子午线轮胎的帘线层数较普通斜交胎少,胎体薄,轮胎在载荷作用下发生变形后所产生的弹性迟滞损失小,因而子午线轮胎的滚动阻力系数f较低,如图3-11所示。
用合成橡胶制成的轮胎,其滚动阻力一般要比用天然橡胶制成的稍大。丁基橡胶轮胎的牵引附着性能较好,而其滚动阻力甚至比普通的合成橡胶轮胎更大。
轮胎充气压力p对滚动阻力系数f值有很大影响。汽车在硬路面上行驶时,若轮胎气压降低,则f值迅速增大(图3-13)。这是因为胎压影响轮胎挠性,在相同大小的载荷作用下,气压降低时轮胎变形大,使轮胎滚动时的迟滞损失增大的缘故。
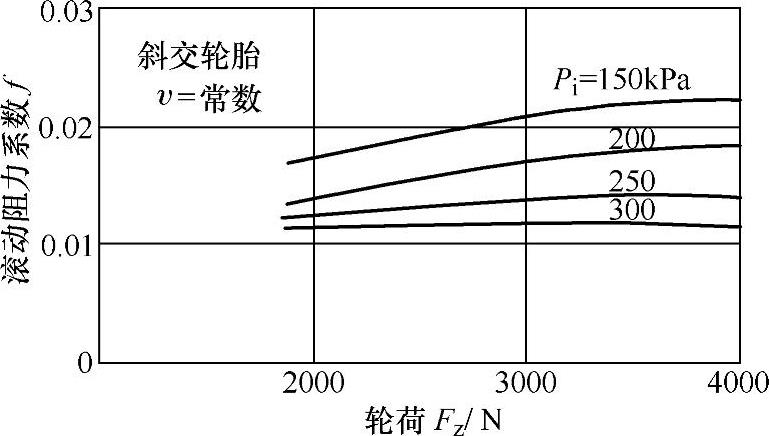
图3-13 气压对滚动阻力系数的影响
胎压对滚动阻力的影响随路面的变形性质而异。在坚硬路面上,滚动阻力随胎压增加而稍有减少。在松软路面上(如砂土路)行驶时,若轮胎气压高,地面变形增加,因而滚动阻力增大;而轮胎气压低时,地面变形减少,轮胎变形增大,因而轮胎弹性迟滞损失增加。因此对某一特定的松软路面,具有一最佳的轮胎气压,此时轮胎变形造成的弹性迟滞损失与路面变形形成的滚动阻力之和最小。
驱动力矩作用于驱动轮,使胎面相对于路面有一定滑动,使轮胎滚动时的能量损失增大,因而滚动阻力系数增大。若用驱动力系数(驱动力与径向载荷之比)表示驱动力的相对大小,滚动阻力系数与驱动力系数的关系如图3-14所示。
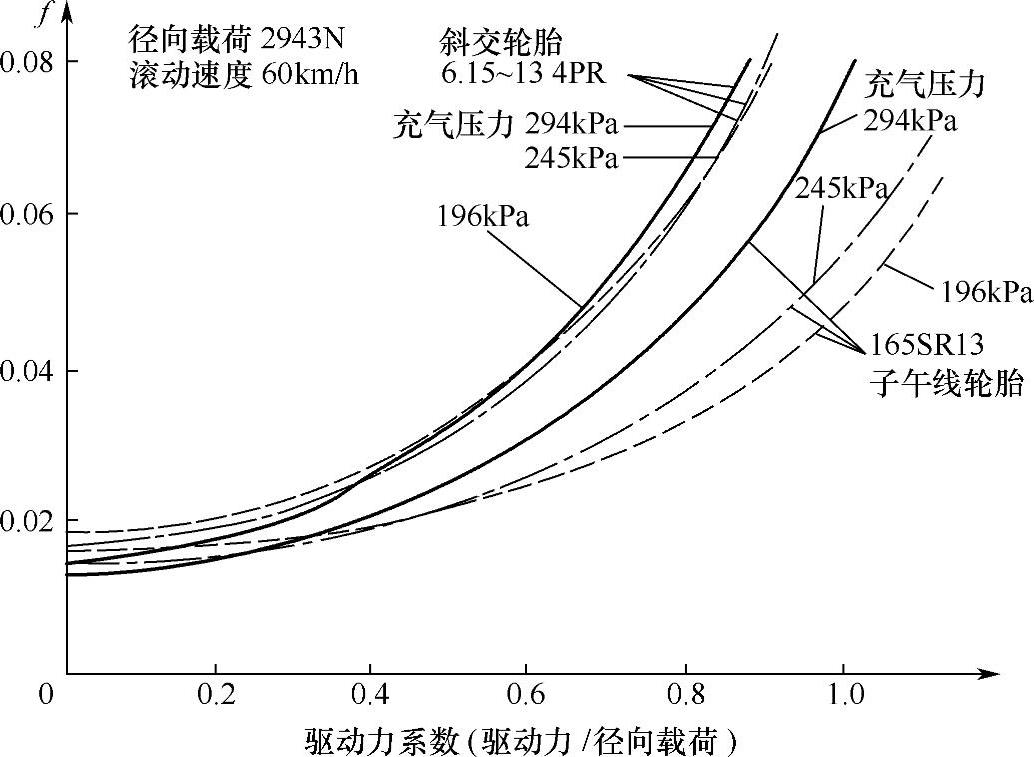
图3-14 滚动阻力系数与驱动力系数的关系
汽车转弯行驶时,轮胎在侧向力作用下发生侧偏现象,轮胎变形及在路面上的滑移增大,因而滚动阻力大幅度增加(图3-15),其增大量可达直线行驶时滚动阻力的50%~100%。工作温度对轮胎的滚动阻力也有影响,图3-16所示为汽车滚动阻力随轮胎内部温度而变化的关系。
进行动力性分析时,一般把滚动阻力系数f看成常数,并取其在良好混凝土或沥青硬路面上的滚动阻力系数值,如轿车可取f=0.0165。也可以用以下经验公式估算滚动阻力系数f的值。
轿车轮胎的滚动阻力系数为
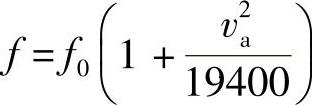
式中,f0=0.014,良好沥青或混凝土路面;f0=0.025,卵石路面;f0=0.20,砂石路面。
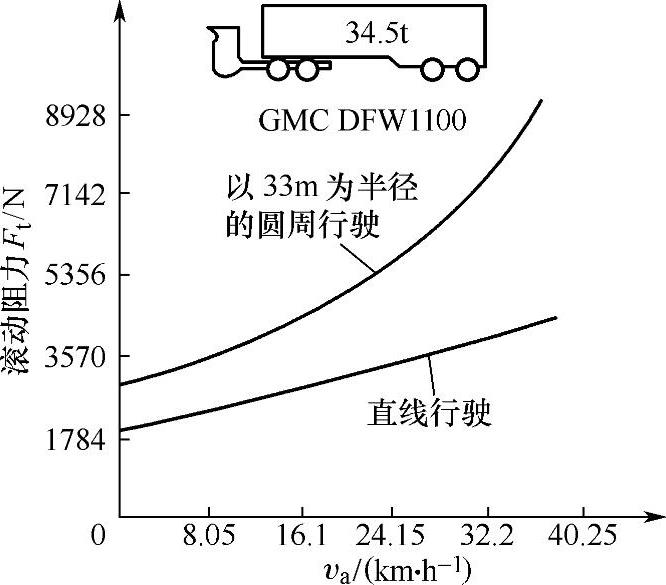
图3-15 汽车转弯行驶时的滚动阻力
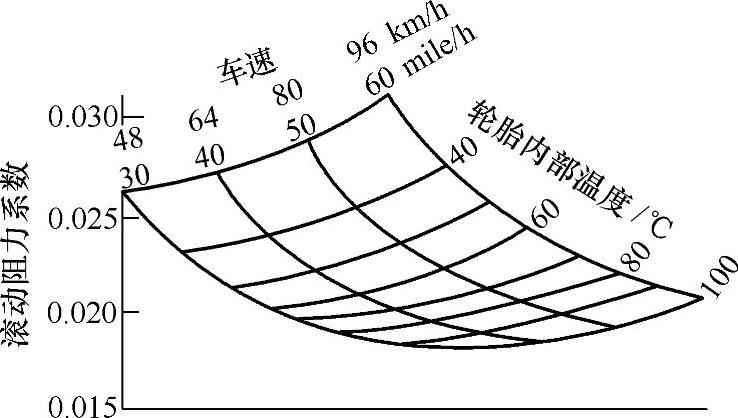
图3-16 轮胎内部温度对滚动阻力系数的影响
货车轮胎气压高,其滚动阻力系数为
f=0.0076+0.000056va
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






