在列车制动荷载和不同连续梁简化方案条件下的各结构纵向力、纵向位移及其最大值分别如图4-27、图4-28和表4-26所示。

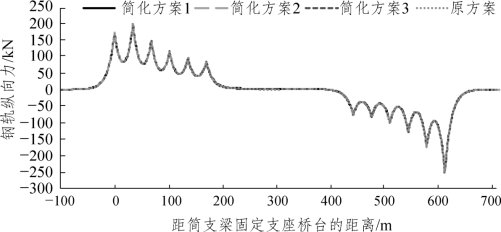
图4-27　列车制动荷载和不同连续梁简化方案条件下钢轨纵向力

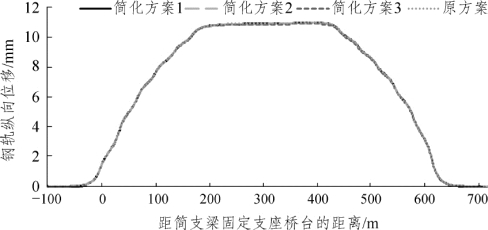
图4-28　列车制动荷载和不同连续梁简化方案条件下钢轨纵向位移(www.daowen.com)

表4-26　列车制动荷载和不同连续梁简化方案条件下结构纵向力与位移的最大值

由图4-27、图4-28和表4-26可知，三种简化的等截面模型与原有变截面模型计算所得的各轨道及桥梁结构纵向力与位移变化趋势及其最大值相差不大，轨道板、自密实混凝土层、凸台、弹性垫层及底座板纵向应力基本不变。相比于原方案的变截面模型，等截面简化模型计算的钢轨最大纵向力变化均小于1 kN，钢轨纵向位移变化均小于0.1 mm，轨板相对位移变化均小于 0.01 mm，其中简化方案1（边跨支点等截面模型）、简化方案2（边跨1/2处等截面模型）和简化方案3（主跨支点等截面模型）计算的固定支座桥台顶纵向力减幅均不足0.1%，固定支座桥墩顶最大纵向力分别减小了0.1%、0.3%和0.4%。由此可知，三种简化的等截面模型与原有变截面模型制动力计算结果误差均不足1%，可满足工程应用的需求，且以简化方案1（边跨支点等截面模型）计算结果的误差最小。

综上所述，本书所提出的三种连续梁简化模型和原有变截面模型伸缩力与制动力计算结果误差均不足1%，可满足工程应用的需求。为了提高计算建模和计算效率，在大跨连续梁桥上CRTSⅢ型板式无砟轨道无缝线路伸缩力与制动力计算过程中，可将变截面的连续梁模型简化成边跨支点等截面模型进行建模计算，以连续箱梁的 3 个特殊断面（边跨支点截面、边跨1/2处截面和主跨支点截面）进行建模均可采用。简化模型挠曲力计算结果与原有模型相差较大，在计算大跨连续梁桥上CRTSⅢ型板式无砟轨道无缝线路挠曲力时必须根据连续梁实际截面参数进行建模计算。考虑到目前广泛应用于高速铁路的大跨连续梁截面大多为箱形截面构造，而箱形截面整体性好、刚度大、列车荷载作用下产生的挠曲变形小，且挠曲力较伸缩力和制动力小很多，所以，在桥梁及轨道结构检算过程中一般采用伸缩力和制动力作为控制因素，而挠曲力一般不会成为控制因素。因此，本书提出的模型简化方案适用于大跨连续梁桥上CRTSⅢ型板式无砟轨道无缝线路的设计检算，采用简化模型可大大提高建模速度和计算效率，且具有一定的通用性。